| Date | November 2012 | Marks available | 4 | Reference code | 12N.2.sl.TZ0.8 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | How much | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows a circular play area for children.
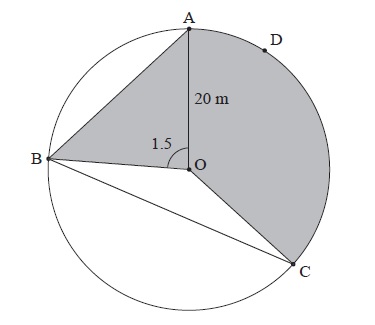
The circle has centre O and a radius of 20 m, and the points A, B, C and D lie on the circle. Angle AOB is 1.5 radians.
Find the length of the chord [AB].
Find the area of triangle AOB.
Angle BOC is 2.4 radians.
Find the length of arc ADC.
Angle BOC is 2.4 radians.
Find the area of the shaded region.
Angle BOC is 2.4 radians.
The shaded region is to be painted red. Red paint is sold in cans which cost \(\$ 32\) each. One can covers \(140{\text{ }}{{\text{m}}^2}\). How much does it cost to buy the paint?
Markscheme
Note: In this question, do not penalise for missing or incorrect units. They are not included in the markscheme, to avoid complex answer lines.
METHOD 1
choosing cosine rule (must have cos in it) (M1)
e.g. \({c^2} = {a^2} + {b^2} - 2ab\cos C\)
correct substitution (into rhs) A1
e.g. \({20^2} + {20^2} - 2(20)(20)\cos 1.5\) , \({\rm{AB}} = \sqrt {800 - 800\cos 1.5} \)
\({\rm{AB = 27}}{\rm{.26555}} \ldots \)
\({\rm{AB}} = 27.3\) \([27.2{\text{, }}27.3]\) A1 N2
[3 marks]
METHOD 2
choosing sine rule (M1)
e.g. \(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\) , \(\frac{{{\rm{AB}}}}{{\sin O}} = \frac{{{\rm{AO}}}}{{\sin B}}\)
correct substitution A1
e.g. \(\frac{{{\rm{AB}}}}{{\sin 1.5}} = \frac{{20}}{{\sin (0.5(\pi - 1.5))}}\)
\({\rm{AB}} = 27.26555 \ldots \)
\({\rm{AB}} = 27.3\) \([27.2{\text{, }}27.3]\) A1 N2
[3 marks]
correct substitution into area formula A1
e.g. \(\frac{1}{2}(20)(20)\sin 1.5\) , \(\frac{1}{2}(20)(27.2655504 \ldots )\sin(0.5(\pi - 1.5))\)
\({\rm{area}} = 199.498997 \ldots \) (accept \(199.75106 = 200\) , from using 27.3)
\({\rm{area}} = 199\) \([199{\text{, }}200]\) A1 N1
[2 marks]
appropriate method to find angle AOC (M1)
e.g. \(2\pi - 1.5 - 2.4\)
correct substitution into arc length formula (A1)
e.g. \((2\pi - 3.9) \times 20\) , \(2.3831853 \ldots \times 20\)
\({\text{arc length}} = 47.6637 \ldots \)
\({\text{arc length}} = 47.7\) \((47.6{\text{, }}47.7]\) (i.e. do not accept \(47.6\)) A1 N2
Notes: Candidates may misread the question and use \({\rm{A}}\widehat {\rm{O}}{\rm{C}} = 2.4\) . If working shown, award M0 then A0MRA1 for the answer 48. Do not then penalize \({\rm{A}}\widehat {\rm{O}}{\rm{C}}\) in part (d) which, if used, leads to the answer \(679.498 \ldots \)
However, if they use the prematurely rounded value of 2.4 for \({\rm{A}}\widehat {\rm{O}}{\rm{C}}\) , penalise 1 mark for premature rounding for the answer 48 in (c). Do not then penalize for this in (d).
[3 marks]
calculating sector area using their angle AOC (A1)
e.g. \(\frac{1}{2}(2.38 \ldots )({20^2})\) , \(200(2.38 \ldots )\) , \(476.6370614 \ldots \)
shaded area = their area of triangle AOB + their area of sector (M1)
e.g. \(199.4989973 \ldots + 476.6370614 \ldots \) , \(199 + 476.637\)
\({\text{shaded area}} = 676.136 \ldots \) (accept \(675.637 \ldots = 676\) from using 199)
\({\text{shaded area}} = 676\) \([676{\text{, }}677]\) A1 N2
[3 marks]
dividing to find number of cans (M1)
e.g. \(\frac{{676}}{{140}}\) , \(4.82857 \ldots \)
5 cans must be purchased (A1)
multiplying to find cost of cans (M1)
e.g. \(5(32)\) , \(\frac{{676}}{{140}} \times 32\)
cost is 160 (dollars) A1 N3
[4 marks]
Examiners report
Candidates generally handled the cosine rule, sectors and arcs well, but some candidates incorrectly treated triangle AOB as a right-angled triangle. A surprising number of candidates changed all angles to degrees and worked with those, often leading to errors in accuracy.
Candidates generally handled the cosine rule, sectors and arcs well, but some candidates incorrectly treated triangle AOB as a right-angled triangle. A surprising number of candidates changed all angles to degrees and worked with those, often leading to errors in accuracy.
In part (c), some candidates misread the question and used 2.4 as the size of angle AOC while others rounded prematurely leading to the inaccurate answer of 48. In either case, marks were lost.
Part (d) proved to be straightforward and candidates were able to obtain full FT marks from errors made in previous parts.
Most candidates had a suitable strategy for part (e) and knew to work with a whole number of cans of paint.

