| Date | November 2013 | Marks available | 6 | Reference code | 13N.2.sl.TZ0.8 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find and Hence or otherwise | Question number | 8 | Adapted from | N/A |
Question
Consider a circle with centre \(\rm{O}\) and radius \(7\) cm. Triangle \(\rm{ABC}\) is drawn such that its vertices are on the circumference of the circle.
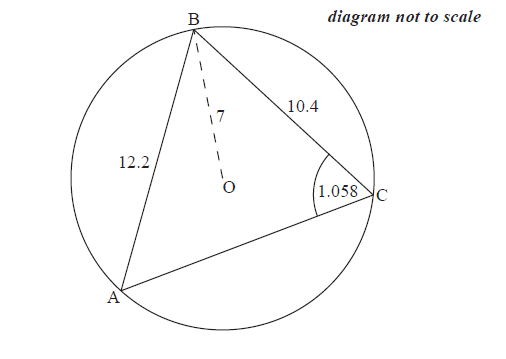
\(\rm{AB}=12.2\) cm, \(\rm{BC}=10.4\) cm and \(\rm{A}\hat{\rm{C}}\rm{B}=1.058\) radians.
Find \({\rm{B\hat AC}}\).
Find \({\text{AC}}\).
Hence or otherwise, find the length of arc \({\text{ABC}}\).
Markscheme
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
evidence of choosing sine rule (M1)
eg \(\frac{{\sin \hat A}}{a} = \frac{{\sin \hat B}}{b}\)
correct substitution (A1)
eg \(\frac{{\sin \hat A}}{{10.4}} = \frac{{\sin 1.058}}{{12.2}}\)
\({\rm{B\hat AC}} = 0.837\) A1 N2
[3 marks]
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
METHOD 1
evidence of subtracting angles from \(\pi \) (M1)
eg \({\rm{A\hat BC}} = \pi - A - C\)
correct angle (seen anywhere) A1
\({\rm{A\hat BC}} = \pi - 1.058 - 0.837,{\text{ }}1.246,{\text{ }}71.4^\circ \)
attempt to substitute into cosine or sine rule (M1)
correct substitution (A1)
eg \({12.2^2} + {10.4^2} - 2 \times 12.2 \times 10.4\cos 71.4,{\text{ }}\frac{{{\text{AC}}}}{{\sin 1.246}} = \frac{{12.2}}{{\sin 1.058}}\)
\({\text{AC}} = 13.3{\text{ (cm)}}\) A1 N3
METHOD 2
evidence of choosing cosine rule M1
eg \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
correct substitution (A2)
eg \({12.2^2} = {10.4^2} + {b^2} - 2 \times 10.4b\cos 1.058\)
\({\text{AC}} = 13.3{\text{ (cm)}}\) A2 N3
[5 marks]
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
METHOD 1
valid approach (M1)
eg \(\cos {\rm{A\hat OC}} = \frac{{{\text{O}}{{\text{A}}^2} + {\text{O}}{{\text{C}}^2} - {\text{A}}{{\text{C}}^2}}}{{2 \times {\text{OA}} \times {\text{OC}}}}\), \({\rm{A\hat OC}} = 2 \times {\rm{A\hat BC}}\)
correct working (A1)
eg \({\text{13.}}{{\text{3}}^2} = {7^2} + {7^2} - 2 \times 7 \times 7\cos {\rm{A\hat OC}},{\text{ }}O = 2 \times 1.246\)
\({\rm{A\hat OC}} = 2.492{\text{ }}(142.8^\circ )\) (A1)
EITHER
correct substitution for arc length (seen anywhere) A1
eg \(2.492 = \frac{l}{7},{\text{ }}l = 17.4,{\text{ }}14\pi \times \frac{{142.8}}{{360}}\)
subtracting arc from circumference (M1)
eg \(2\pi r - l,{\text{ }}14\pi = 17.4\)
OR
attempt to find \({\rm{A\hat OC}}\) reflex (M1)
eg \(2\pi - 2.492,{\text{ }}3.79,{\text{ }}360 - 142.8\)
correct substitution for arc length (seen anywhere) A1
eg \(l = 7 \times 3.79,{\text{ }}14\pi \times \frac{{217.2}}{{360}}\)
THEN
\({\text{arc ABC}} = 26.5\) A1 N4
METHOD 2
valid approach to find \({\rm{A\hat OB}}\) or \({\rm{B\hat OC}}\) (M1)
eg choosing cos rule, twice angle at circumference
correct working for finding one value, \({\rm{A\hat OB}}\) or \({\rm{B\hat OC}}\) (A1)
eg \(\cos {\rm{A\hat OB}} = \frac{{{7^2} + {7^2} - {{12.2}^2}}}{{2 \times 7 \times 7}}\), \({\rm{A\hat OB}} = 2.116,{\rm{B\hat OC}} = 1.6745\)
two correct calculations for arc lengths
eg \({\text{AB}} = 7 \times 2 \times 1.058{\text{ }}( = 14.8135),{\text{ }}7 \times 1.6745{\text{ }}( = 11.7216)\) (A1)(A1)
adding their arc lengths (seen anywhere)
eg \(r{\rm{A\hat OB}} + r{\rm{B\hat OC}},{\text{ }}14.8135 + 11.7216,{\text{ }}7(2.116 + 1.6745)\) M1
\({\text{arc ABC}} = 26.5{\text{ (cm)}}\) A1 N4
Note: Candidates may work with other interior triangles using a similar method. Check calculations carefully and award marks in line with markscheme.
[6 marks]

