| Date | May 2012 | Marks available | 4 | Reference code | 12M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
The following diagram shows a triangle ABC.
\({\rm{BC}} = 6\) , \({\rm{C}}\widehat {\rm{A}}{\rm{B}} = 0.7\) radians , \({\rm{AB}} = 4p\) , \({\rm{AC}} = 5p\) , where \(p > 0\) .
Consider the circle with centre B that passes through the point C. The circle cuts the line CA at D, and \({\rm{A}}\widehat {\rm{D}}{\rm{B}}\) is obtuse. Part of the circle is shown in the following diagram.
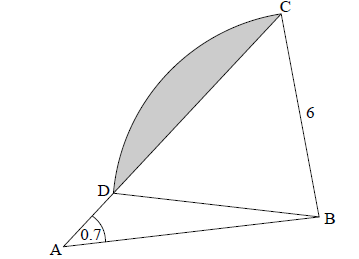
(i) Show that \({p^2}(41 - 40\cos 0.7) = 36\) .
(ii) Find p .
Write down the length of BD.
Find \({\rm{A}}\widehat {\rm{D}}{\rm{B}}\) .
(i) Show that \({\rm{C}}\widehat {\rm{B}}{\rm{D}} = 1.29\) radians, correct to 2 decimal places.
(ii) Hence, find the area of the shaded region.
Markscheme
(i) evidence of valid approach (M1)
e.g. choosing cosine rule
correct substitution (A1)
e.g. \({6^2} = {(5p)^2} + {(4p)^2} - 2 \times (4p) \times (5p)\cos 0.7\)
simplification A1
e.g. \(36 = 25{p^2} + 16{p^2} - 40{p^2}\cos 0.7\)
\({p^2}(41 - 40\cos 0.7) = 36\) AG N0
(ii) \(1.85995 \ldots \)
\(p = 1.86\) A1 N1
Note: Award A0 for \(p = \pm 1.86\) , i.e. not rejecting the negative value.
[4 marks]
\({\text{BD}} = 6\) A1 N1
[1 mark]
evidence of valid approach (M1)
e.g. choosing sine rule
correct substitution A1
e.g. \(\frac{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{B}}}}{{4p}} = \frac{{\sin 0.7}}{6}\)
\({\text{acute }}{\rm{A}}\widehat {\rm{D}}{\rm{B = 0}}{\rm{.9253166}} \ldots \) (A1)
\(\pi - 0.9253166 \ldots = 2.216275 \ldots \)
\({\rm{A}}\widehat {\rm{D}}{\rm{B}} = 2.22\) A1 N3
[4 marks]
(i) evidence of valid approach (M1)
e.g. recognize isosceles triangle, base angles equal
\(\pi - 2(0.9253 \ldots )\) A1
\({\rm{C}}\widehat {\rm{B}}{\rm{D}} = 1.29\) AG N0
(ii) area of sector BCD (A1)
e.g. \(0.5 \times (1.29) \times {(6)^2}\)
area of triangle BCD (A1)
e.g. \(0.5 \times {(6)^2}\sin 1.29\)
evidence of subtraction M1
\(5.92496 \ldots \)
\(5.937459 \ldots \)
\({\text{area}} = 5.94\) A1 N3
[6 marks]
Examiners report
There were mixed results with this question. Most candidates could access part (a) and made the correct choice with the cosine rule but sloppy notation often led to candidates not being able to show the desired result.
There were mixed results with this question. Most candidates could access part (a) and made the correct choice with the cosine rule but sloppy notation often led to candidates not being able to show the desired result.
In part (c), candidates again correctly identified an appropriate method but failed to recognize that their result of 0.925 was acute and not obtuse as required.
In (d) (i), many attempted to use the sine rule under the incorrect assumption that DC was equal to 5p, rather than rely on some basic isosceles triangle geometry. Consequently, the result of 1.29 for \({\rm{C}}\widehat {\rm{B}}{\rm{D}}\) was not easy to show. There was a great deal of success with (d) (ii) with candidates using appropriate techniques to find the area of the shaded region although some stopped after finding the area of the sector.

