| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.sl.TZ1.3 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows three towns A, B and C. Town B is 5 km from Town A, on a bearing of 070°. Town C is 8 km from Town B, on a bearing of 115°.
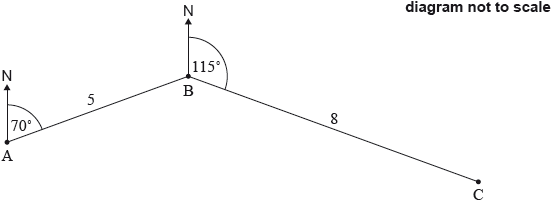
Find \({\rm{A\hat BC}}\).
Find the distance from Town A to Town C.
Use the sine rule to find \({\rm{A\hat CB}}\).
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(70 + (180 - 115),{\text{ }}360 - (110 + 115)\)
\({\rm{A\hat BC}} = 135^\circ \) A1 N2
[2 marks]
choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({c^2} = {a^2} + {b^2} - 2ab\cos C\)
correct substitution into RHS (A1)
eg\(\,\,\,\,\,\)\({5^2} + {8^2} - 2 \times 5 \times 8\cos 135\)
12.0651
12.1 (km) A1 N2
[3 marks]
correct substitution (must be into sine rule) A1
eg\(\,\,\,\,\,\)\(\frac{{\sin {\rm{A\hat CB}}}}{5} = \frac{{\sin 135}}{{{\text{AC}}}}\)
17.0398
\({\rm{A\hat CB}} = 17.0\) A1 N1
[2 marks]
Examiners report
Some candidates tackled this question very competently, whilst others struggled to obtain a correct answer even for part (a) which would generally be regarded as prior learning.
Parts (b) and (c) were generally answered well, even with follow through from an incorrect angle in part (a). Weaker candidates assumed the triangle to be a right triangle and attempted to use Pythagoras to find AC. One of the most significant errors seen throughout this question was with candidates substituting an angle in degrees into a calculator set in radian mode.
Parts (b) and (c) were generally answered well, even with follow through from an incorrect angle in part (a). Weaker candidates assumed the triangle to be a right triangle and attempted to use Pythagoras to find AC. One of the most significant errors seen throughout this question was with candidates substituting an angle in degrees into a calculator set in radian mode.

