IB Questionbank

User interface language: English | Español

Date	May 2016	Marks available	4	Reference code	16M.3srg.hl.TZ0.1
Level	HL only	Paper	Paper 3 Sets, relations and groups	Time zone	TZ0
Command term	Solve	Question number	1	Adapted from	N/A

Question

, is defined on the set $S = \{ 1,{\text{ }}2,{\text{ }}4,{\text{ }}5,{\text{ }}7,{\text{ }}8\}$ .

Copy and complete the table.

[3]

Show that $\{ S,{\text{ }} * \}$ is an Abelian group.

[5]

Determine the orders of all the elements of $\{ S,{\text{ }} * \}$ .

[3]

(i) Find the two proper subgroups of $\{ S,{\text{ }} * \}$ .

(ii) Find the coset of each of these subgroups with respect to the element 5.

[4]

Solve the equation $2 * x * 4 * x * 4 = 2$ .

[4]

Markscheme

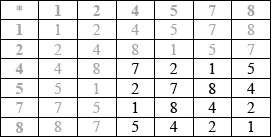M16/5/MATHL/HP3/ENG/TZ0/SG/M/01.a A3

Note: Award A3 for correct table, A2 for one or two errors, A1 for three or four errors and A0 otherwise.

[3 marks]

the table contains only elements of $S$ , showing closure R1

the identity is 1 A1

every element has an inverse since 1 appears in every row and column, or a complete list of elements and their correct inverses A1

multiplication of numbers is associative A1

the four axioms are satisfied therefore $\{ S,{\text{ }} * \}$ is a group

the group is Abelian because the table is symmetric (about the leading diagonal) A1

[5 marks]

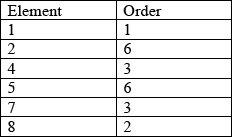M16/5/MATHL/HP3/ENG/TZ0/SG/M/01.c A3

Note: Award A3 for all correct values, A2 for 5 correct, A1 for 4 correct and A0 otherwise.

[3 marks]

(i) the subgroups are $\{ 1,{\text{ }}8\}$ ; $\{ 1,{\text{ }}4,{\text{ }}7\}$ A1A1

(ii) the cosets are $\{ 4,{\text{ }}5\}$ ; $\{ 2,{\text{ }}5,{\text{ }}8\}$ A1A1

[4 marks]

METHOD 1

use of algebraic manipulations M1

and at least one result from the table, used correctly A1

$x = 2$ A1

$x = 7$ A1

METHOD 2

testing at least one value in the equation M1

obtain $x = 2$ A1

obtain $x = 7$ A1

explicit rejection of all other values A1

[4 marks]

Examiners report

The majority of candidates were able to complete the Cayley table correctly.

Generally well done. However, it is not good enough for a candidate to say something along the lines of 'the operation is closed or that inverses exist by looking at the Cayley table'. A few candidates thought they only had to prove commutativity.

Often well done. A few candidates stated extra, and therefore incorrect subgroups.

[N/A]

The majority found only one solution, usually the obvious $x = 2$ , but sometimes only the less obvious $x = 7$ .

Syllabus sections

Topic 8 - Option: Sets, relations and groups

Show 211 related questions

16M.3srg.hl.TZ0.1a: Copy and complete the table.
16M.3srg.hl.TZ0.1b: Show that $\{ S,{\text{ }} * \}$ is an Abelian group.
16M.3srg.hl.TZ0.1c: Determine the orders of all the elements of $\{ S,{\text{ }} * \}$ .
16M.3srg.hl.TZ0.1d: (i) Find the two proper subgroups of $\{ S,{\text{ }} * \}$ . (ii) Find the coset...
16M.3srg.hl.TZ0.2a: Show that $R$ is an equivalence relation.
16M.3srg.hl.TZ0.2b: Given that $n = 2$ and $p = 7$ , determine the first four members of each of the four...
16M.3srg.hl.TZ0.3: The group $\{ G,{\text{ }} * \}$ is Abelian and the bijection $f:{\text{ }}G \to G$ is...
16M.3srg.hl.TZ0.4a: Prove that $f$ is an injection.
16M.3srg.hl.TZ0.5: The group $\{ G,{\text{ }} * \}$ is defined on the set $G$ with binary operation \( *...
16M.3srg.hl.TZ0.4b: (i) Prove that $f$ is a surjection. (ii) Hence, or otherwise, write down the...
17N.3srg.hl.TZ0.5b: Prove that ${\text{Ker}}(f)$ is a subgroup of $\{ G,{\text{ }} * \}$ .
17N.3srg.hl.TZ0.5a: Prove that $f({e_G}) = {e_H}$ .
17N.3srg.hl.TZ0.4d: Show that each element $a \in S$ has an inverse.
17N.3srg.hl.TZ0.4c: Show that 2 is the identity element.
17N.3srg.hl.TZ0.4b.i: Show that the operation $*$ on the set $S$ is commutative.
17N.3srg.hl.TZ0.4a: Show that $x * y \in S$ for all $x,{\text{ }}y \in S$ .
17N.3srg.hl.TZ0.3b: Determine the equivalence class of R containing the element $(1,{\text{ }}2)$ and...
17N.3srg.hl.TZ0.3a: Show that R is an equivalence relation.
17N.3srg.hl.TZ0.2b.ii: In the context of the distributive law, describe what the result in part (b)(i) illustrates.
17N.3srg.hl.TZ0.2b.i: For sets $P$ , $Q$ and $R$ , verify that...
17N.3srg.hl.TZ0.2a.ii: Represent the following set on a Venn diagram, $A \cap (B \cup C)$ .
17N.3srg.hl.TZ0.2a.i: Represent the following set on a Venn diagram, $A\Delta B$ , the symmetric difference of...
17N.3srg.hl.TZ0.1c: Find the left cosets of $K$ in $\{ G,{\text{ }}{ \times _{18}}\}$ .
17N.3srg.hl.TZ0.1b: Write down the elements in set $K$ .
17N.3srg.hl.TZ0.1a.ii: State whether or not $\{ G,{\text{ }}{ \times _{18}}\}$ is cyclic, justifying your answer.
17N.3srg.hl.TZ0.1a.i: Find the order of elements 5, 7 and 17 in $\{ G,{\text{ }}{ \times _{18}}\}$ .
17M.3srg.hl.TZ0.4d: Show that the groups $\{ \mathbb{Z},{\text{ }} * \}$ and...
17M.3srg.hl.TZ0.4c: Find a proper subgroup of $\{ \mathbb{Z},{\text{ }} * \}$ .
17M.3srg.hl.TZ0.4b: Show that there is no element of order 2.
17M.3srg.hl.TZ0.4a: Show that $\{ \mathbb{Z},{\text{ }} * \}$ is an Abelian group.
17M.3srg.hl.TZ0.3b: Hence write down the inverse function ${f^{ - 1}}(x,{\text{ }}y)$ .
17M.3srg.hl.TZ0.3a: Show that $f$ is a bijection.
17M.3srg.hl.TZ0.2b: Determine the number of equivalence classes of $S$ .
17M.3srg.hl.TZ0.2a.ii: Determine the equivalence classes of $R$ .
17M.3srg.hl.TZ0.1b.ii: Hence by considering $A \cap (B \cup C)$ , verify that in this case the operation $\cap$ ...
17M.3srg.hl.TZ0.1b.i: Write down all the elements of $A \cap B,{\text{ }}A \cap C$ and $B \cup C$ .
17M.3srg.hl.TZ0.1a.ii: Determine the symmetric difference, $A\Delta B$ , of the sets $A$ and $B$ .
17M.3srg.hl.TZ0.1a.i: Write down all the elements of $A$ and all the elements of $B$ .
15N.3srg.hl.TZ0.5c: Prove that $\{ {\text{Ker}}(f),{\text{ }} + \}$ is a subgroup of...
15N.3srg.hl.TZ0.5b: Find the kernel of $f$ .
15N.3srg.hl.TZ0.5a: Prove that the function $f$ is a homomorphism from the group...
15N.3srg.hl.TZ0.4c: Find the order of each element in $T$ .
15N.3srg.hl.TZ0.4b: Prove that $\{ T,{\text{ }} * \}$ forms an Abelian group.
15N.3srg.hl.TZ0.4a: Copy and complete the following Cayley table for $\{ T,{\text{ }} * \}$ .
15N.3srg.hl.TZ0.3d: (i) Find the maximum possible order of an element in $\{ H,{\text{ }} \circ \}$ . (ii)...
15N.3srg.hl.TZ0.3c: Find (i) $p \circ p$ ; (ii) the inverse of $p \circ p$ .
15N.3srg.hl.TZ0.3b: State the identity element in $\{ G,{\text{ }} \circ \}$ .
15N.3srg.hl.TZ0.3a: Find the order of $\{ G,{\text{ }} \circ \}$ .
15N.3srg.hl.TZ0.2c: The relation $R$ is defined for $a,{\text{ }}b \in \mathbb{R}$ so that $aRb$ if and...
15N.3srg.hl.TZ0.2b: The relation $R$ is defined for $a,{\text{ }}b \in \mathbb{R}$ so that $aRb$ if and...
15N.3srg.hl.TZ0.1: Given the sets $A$ and $B$ , use the properties of sets to prove that...
12M.3srg.hl.TZ0.1a: Associativity and commutativity are two of the five conditions for a set S with the binary...
12M.3srg.hl.TZ0.1b: The Cayley table for the binary operation $\odot$ defined on the set T = {p, q, r, s,...
12M.3srg.hl.TZ0.2a: Given that $R = (P \cap Q')'$ , list the elements of R .
12M.3srg.hl.TZ0.2b: For a set S , let ${S^ * }$ denote the set of all subsets of S , (i) find \({P^ *...
12M.3srg.hl.TZ0.3a: Show that R is an equivalence relation.
12M.3srg.hl.TZ0.3b: Find the equivalence class containing 0.
12M.3srg.hl.TZ0.3c: Denote the equivalence class containing n by Cn . List the first six elements of ${C_1}$ .
12M.3srg.hl.TZ0.3d: Denote the equivalence class containing n by Cn . Prove that ${C_n} = {C_{n + 7}}$ for all...
12M.3srg.hl.TZ0.4b: The set S is finite. If the function $f:S \to S$ is injective, show that f is surjective.
12M.3srg.hl.TZ0.5a: (i) Show that $gh{g^{ - 1}}$ has order 2 for all $g \in G$ . (ii) Deduce that gh...
12N.3srg.hl.TZ0.1a: Decide, giving a proof or a counter-example, whether $xRy \Leftrightarrow x + y > 7$ ...
12N.3srg.hl.TZ0.1d: Decide, giving a proof or a counter-example, whether...
12N.3srg.hl.TZ0.1b: Decide, giving a proof or a counter-example, whether...
12N.3srg.hl.TZ0.1c: Decide, giving a proof or a counter-example, whether $xRy \Leftrightarrow xy > 0$ ...
12N.3srg.hl.TZ0.3e: (i) State the identity element for $\{ P(S){\text{, }}\Delta \}$ . (ii) Write down...
12N.3srg.hl.TZ0.1e: One of the relations from parts (a), (b), (c) and (d) is an equivalence relation. For this...
12N.3srg.hl.TZ0.3a: Write down all four subsets of A .
12N.3srg.hl.TZ0.3b: Construct the Cayley table for $P(A)$ under $\Delta$ .
12N.3srg.hl.TZ0.3c: Prove that $\left\{ {P(A),{\text{ }}\Delta } \right\}$ is a group. You are allowed to...
12N.3srg.hl.TZ0.3d: Is $\{ P(A){\text{, }}\Delta \}$ isomorphic to $\{ {\mathbb{Z}_4},{\text{ }}{ + _4}\}$ ...
12N.3srg.hl.TZ0.3f: Explain why $\{ P(S){\text{, }} \cup \}$ is not a group.
12N.3srg.hl.TZ0.3g: Explain why $\{ P(S){\text{, }} \cap \}$ is not a group.
12N.3srg.hl.TZ0.4a: Simplify $\frac{c}{2} * \frac{{3c}}{4}$ .
12N.3srg.hl.TZ0.4b: State the identity element for G under $*$ .
12N.3srg.hl.TZ0.4c: For $x \in G$ find an expression for ${x^{ - 1}}$ (the inverse of x under $*$ ).
12N.3srg.hl.TZ0.4d: Show that the binary operation $*$ is commutative on G .
12N.3srg.hl.TZ0.4e: Show that the binary operation $*$ is associative on G .
12N.3srg.hl.TZ0.4g: Show that G is closed under $*$ .
12N.3srg.hl.TZ0.4h: Explain why $\{ G, * \}$ is an Abelian group.
08M.3srg.hl.TZ1.1: (a) Determine whether or not $*$ is (i) closed, (ii) commutative, (iii) ...
08M.3srg.hl.TZ1.2: (a) Find the range of f . (b) Prove that f is an injection. (c) Taking the...
08M.3srg.hl.TZ1.3: (a) Find the six roots of the equation ${z^6} - 1 = 0$ , giving your answers in the...
08M.3srg.hl.TZ1.4: (a) Show that R is an equivalence relation. (b) Describe, geometrically, the...
08M.3srg.hl.TZ1.5: Let $p = {2^k} + 1,{\text{ }}k \in {\mathbb{Z}^ + }$ be a prime number and let G be the...
08M.3srg.hl.TZ2.1: (a) Draw the Cayley table for the set of integers G = {0, 1, 2, 3, 4, 5} under addition...
08M.3srg.hl.TZ2.2a: Below are the graphs of the two functions $F:P \to Q{\text{ and }}g:A \to B$ ...
08M.3srg.hl.TZ2.2b: Given two functions $h:X \to Y{\text{ and }}k:Y \to Z$ . Show that (i) if both h and...
08M.3srg.hl.TZ2.4a: The relation aRb is defined on {1, 2, 3, 4, 5, 6, 7, 8, 9} if and only if ab is the square of...
08M.3srg.hl.TZ2.4b: Given the group $(G,{\text{ }} * )$ , a subgroup $(H,{\text{ }} * )$ and...
08M.3srg.hl.TZ2.5: (a) Write down why the table below is a Latin...
08M.3srg.hl.TZ2.3: Prove that $(A \cap B)\backslash (A \cap C) = A \cap (B\backslash C)$ where A, B and C are...
08N.3srg.hl.TZ0.1: $A$ , $B$ , $C$ and $D$ are subsets of $\mathbb{Z}$ ...
08N.3srg.hl.TZ0.2: A binary operation is defined on {−1, 0, 1}...
08N.3srg.hl.TZ0.5: Three functions mapping $\mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}$ are defined...
08N.3srg.hl.TZ0.3: Two functions, F and G , are defined on $A = \mathbb{R}\backslash \{ 0,{\text{ }}1\}$ ...
08N.3srg.hl.TZ0.4: Determine, giving reasons, which of the following sets form groups under the operations given...
11M.3srg.hl.TZ0.1a: Copy and complete the following operation table.
11M.3srg.hl.TZ0.1b: (i) Show that {S , $*$ } is a group. (ii) Find the order of each element of {S ,...
11M.3srg.hl.TZ0.1c: The set T is defined by $\{ x * x:x \in S\}$ . Show that {T , $*$ } is a subgroup of {S...
11M.3srg.hl.TZ0.2a: A \ B ;
11M.3srg.hl.TZ0.3a: Show that R is an equivalence relation.
11M.3srg.hl.TZ0.4: The function...
11M.3srg.hl.TZ0.5b: Consider the group G , of order 4, which has distinct elements a , b and c and the identity...
11M.3srg.hl.TZ0.2b: $A\Delta B$ .
11M.3srg.hl.TZ0.3b: Identify the three equivalence classes.
11M.3srg.hl.TZ0.5a: Given that p , q and r are elements of a group, prove the left-cancellation rule, i.e....
09M.3srg.hl.TZ0.1: (a) Show that {1, −1, i, −i} forms a group of complex numbers G under...
09M.3srg.hl.TZ0.2a: (i) Show that $*$ is commutative. (ii) Find the identity element. (iii) ...
09M.3srg.hl.TZ0.2b: The binary operation $\cdot$ is defined on $\mathbb{R}$ as follows. For any elements a...
09M.3srg.hl.TZ0.3: The relation R is defined on $\mathbb{Z} \times \mathbb{Z}$ such that...
09M.3srg.hl.TZ0.4: (a) Show that $f:\mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}$ defined...
09M.3srg.hl.TZ0.5: Prove that set difference is not associative.
09N.3srg.hl.TZ0.1: The binary operation $*$ is defined on the set S = {0, 1, 2, 3}...
09N.3srg.hl.TZ0.2: The function $f:[0,{\text{ }}\infty [ \to [0,{\text{ }}\infty [$ is defined by...
09N.3srg.hl.TZ0.3: The relations R and S are defined on quadratic polynomials P of the...
09N.3srg.hl.TZ0.5: Let {G , $*$ } be a finite group of order n and let H be a non-empty subset of G . (a) ...
SPNone.3srg.hl.TZ0.1a: The relation R is defined on ${\mathbb{Z}^ + }$ by aRb if and only if ab is even. Show that...
SPNone.3srg.hl.TZ0.1b: The relation S is defined on ${\mathbb{Z}^ + }$ by aSb if and only if...
SPNone.3srg.hl.TZ0.2c: $*$ is distributive over $\odot$ ;
SPNone.3srg.hl.TZ0.2a: $\odot$ is commutative;
SPNone.3srg.hl.TZ0.2b: $*$ is associative;
SPNone.3srg.hl.TZ0.2d: $\odot$ has an identity element.
SPNone.3srg.hl.TZ0.3a: (i) Write down the Cayley table for $\{ G,{\text{ }}{ \times _7}\}$ . (ii) ...
SPNone.3srg.hl.TZ0.3b: The group $\{ K,{\text{ }} \circ \}$ is defined on the six permutations of the integers 1,...
SPNone.3srg.hl.TZ0.4: The groups $\{ K,{\text{ }} * \}$ and $\{ H,{\text{ }} \odot \}$ are defined by the...
SPNone.3srg.hl.TZ0.5: Let $\{ G,{\text{ }} * \}$ be a finite group and let H be a non-empty subset of G . Prove...
10M.3srg.hl.TZ0.3: (a) Consider the set A = {1, 3, 5, 7} under the binary operation $*$ , where $*$ ...
10M.3srg.hl.TZ0.4: The permutation ${p_1}$ of the set {1, 2, 3, 4} is defined...
10M.3srg.hl.TZ0.5: Let G be a finite cyclic group. (a) Prove that G is Abelian. (b) Given that a is a...
10M.3srg.hl.TZ0.1: The function $f:\mathbb{R} \to \mathbb{R}$ is defined...
10N.3srg.hl.TZ0.1: Let R be a relation on the set $\mathbb{Z}$ such that...
10N.3srg.hl.TZ0.2a: Let...
10N.3srg.hl.TZ0.2b: P is the set of all polynomials such that...
10N.3srg.hl.TZ0.2c: Let $h:\mathbb{Z} \to {\mathbb{Z}^ + }$ ,...
10N.3srg.hl.TZ0.4: Set...
10N.3srg.hl.TZ0.5: Let $\{ G,{\text{ }} * \}$ be a finite group that contains an element a (that is not the...
13M.3srg.hl.TZ0.1b: is commutative;
13M.3srg.hl.TZ0.1c: is associative;
13M.3srg.hl.TZ0.2a: Copy and complete the following Cayley table for this binary operation.
13M.3srg.hl.TZ0.2c: Show that a new set G can be formed by removing one of the elements of S such that...
13M.3srg.hl.TZ0.2d: Determine the order of each element of $\{ G,{\text{ }}{ \times _{14}}\}$ .
13M.3srg.hl.TZ0.2e: Find the proper subgroups of $\{ G,{\text{ }}{ \times _{14}}\}$ .
13M.3srg.hl.TZ0.4b: Show that the equivalence defining R can be written in the...
13M.3srg.hl.TZ0.4c: Hence, or otherwise, determine the equivalence classes.
13M.3srg.hl.TZ0.1a: is closed;
13M.3srg.hl.TZ0.1d: has an identity element.
13M.3srg.hl.TZ0.2b: Give one reason why $\{ S,{\text{ }}{ \times _{14}}\}$ is not a group.
13M.3srg.hl.TZ0.3a: (i) Sketch the graph of f. (ii) By referring to your graph, show that f is a bijection.
13M.3srg.hl.TZ0.3b: Find ${f^{ - 1}}(x)$ .
13M.3srg.hl.TZ0.4a: Show that R is an equivalence relation.
13M.3srg.hl.TZ0.5: H and K are subgroups of a group G. By considering the four group axioms, prove that...
11N.3srg.hl.TZ0.1a: Consider the following Cayley table for the set G = {1, 3, 5, 7, 9, 11, 13, 15} under the...
11N.3srg.hl.TZ0.1b: The Cayley table for the set...
11N.3srg.hl.TZ0.1c: Show that $\{ G,{\text{ }}{ \times _{16}}\}$ and $\{ H,{\text{ }} * \}$ are not...
11N.3srg.hl.TZ0.1d: Show that $\{ H,{\text{ }} * \}$ is not cyclic.
11N.3srg.hl.TZ0.2a: Determine, using Venn diagrams, whether the following statements are true. (i) ...
11N.3srg.hl.TZ0.2b: Prove, without using a Venn diagram, that $A\backslash B$ and $B\backslash A$ are...
11N.3srg.hl.TZ0.4a: Show that R is an equivalence relation.
11N.3srg.hl.TZ0.4b: The Cayley table for G is shown below. The subgroup H is given as...
11N.3srg.hl.TZ0.5a: Show that if both f and g are injective, then $g \circ f$ is also injective.
11N.3srg.hl.TZ0.5b: Show that if both f and g are surjective, then $g \circ f$ is also surjective.
11N.3srg.hl.TZ0.5c: Show, using a single counter example, that both of the converses to the results in part (a)...
12M.3srg.hl.TZ0.4a: The function $g:\mathbb{Z} \to \mathbb{Z}$ is defined by...
12M.3srg.hl.TZ0.4c: Using the set ${\mathbb{Z}^ + }$ as both domain and codomain, give an example of an...
14M.3srg.hl.TZ0.2a: (i) Write down the six smallest non-negative elements of $S$ . (ii) Show that...
14M.3srg.hl.TZ0.2b: The relation $R$ is defined on $S$ by ${s_1}R{s_2}$ if...
14M.3srg.hl.TZ0.3a: (i) Sketch the set $X \times Y$ in the Cartesian plane. (ii) Sketch the set...
14M.3srg.hl.TZ0.4b: (i) Prove that the kernel of $f,{\text{ }}K = {\text{Ker}}(f)$ , is closed under the...
14M.3srg.hl.TZ0.1: The binary operation $\Delta$ is defined on the set $S =$ {1, 2, 3, 4, 5} by the...
14M.3srg.hl.TZ0.3b: Consider the function $f:X \times Y \to \mathbb{R}$ defined by $f(x,{\text{ }}y) = x + y$ ...
14M.3srg.hl.TZ0.4c: (i) Prove that $gk{g^{ - 1}} \in K$ for all $g \in G,{\text{ }}k \in K$ . (ii) ...
13N.3srg.hl.TZ0.2a: (i) Prove that $G$ is cyclic and state two of its generators. (ii) Let $H$ be...
13N.3srg.hl.TZ0.2b: State, with a reason, whether or not it is necessary that a group is cyclic given that all...
13N.3srg.hl.TZ0.1: Consider the following functions ...
13N.3srg.hl.TZ0.4: Let $(H,{\text{ }} * {\text{)}}$ be a subgroup of the group \((G,{\text{ }} *...
13N.3srg.hl.TZ0.5: (a) Given a set $U$ , and two of its subsets $A$ and $B$ , prove...
14M.3srg.hl.TZ0.4a: Prove that $f({e_G}) = {e_H}$ , where ${e_G}$ is the identity element in $G$ and...
15M.3srg.hl.TZ0.3b: Hence prove that $R$ is reflexive.
15M.3srg.hl.TZ0.4a: Prove that: (i) $f$ is an injection, (ii) $g$ is a surjection.
15M.3srg.hl.TZ0.2a: Find the element $e$ such that $e * y = y$ , for all $y \in S$ .
15M.3srg.hl.TZ0.2b: (i) Find the least solution of $x * x = e$ . (ii) Deduce that $(S,{\text{ }} * )$ ...
15M.3srg.hl.TZ0.3d: Find the set of all $y$ for which $3Ry$ .
15M.3srg.hl.TZ0.3e: Using your answers for (c) and (d) show that $R$ is not symmetric.
15M.3srg.hl.TZ0.1a: Complete the following Cayley table [5 marks]
15M.3srg.hl.TZ0.1b: (i) State the inverse of each element. (ii) Determine the order of each element.
15M.3srg.hl.TZ0.1c: Write down the subgroups containing (i) $r$ , (ii) $u$ .
15M.3srg.hl.TZ0.2c: Determine whether or not $e$ is an identity element.
15M.3srg.hl.TZ0.3a: Show that the product of three consecutive integers is divisible by $6$ .
15M.3srg.hl.TZ0.3c: Find the set of all $y$ for which $5Ry$ .
15M.3srg.hl.TZ0.4b: Given that $X = {\mathbb{R}^ + } \cup \{ 0\}$ and $Y = \mathbb{R}$ , choose a suitable...
15M.3srg.hl.TZ0.5a: Show that $(G,{\text{ }} + )$ forms a group where $+$ denotes addition on...
15M.3srg.hl.TZ0.5b: Assuming that $(H,{\text{ }} + )$ forms a group, show that it is a proper subgroup of...
15M.3srg.hl.TZ0.5c: The mapping $\phi :G \to G$ is given by $\phi (g) = g + g$ , for $g \in G$ . Prove that...
14N.3srg.hl.TZ0.1b: Find the order of each of the elements of the group.
14N.3srg.hl.TZ0.1c: Write down the three sets that form subgroups of order 2.
14N.3srg.hl.TZ0.5c: Let $\{ H,{\rm{ }} * {\rm{\} }}$ be a subgroup of $\{ G,{\rm{ }} * {\rm{\} }}$ . Let $R$ ...
14N.3srg.hl.TZ0.1a: Find the values represented by each of the letters in the table.
14N.3srg.hl.TZ0.1d: Find the three sets that form subgroups of order 4.
14N.3srg.hl.TZ0.2b: Prove that $f$ is not a surjection.
14N.3srg.hl.TZ0.2a: Prove that $f$ is an injection.
14N.3srg.hl.TZ0.3a: Two members of $A$ are given by $p = (1{\text{ }}2{\text{ }}5)$ and...
14N.3srg.hl.TZ0.4c: Given that $f(x * y) = p$ , find $f(y)$ .
14N.3srg.hl.TZ0.3b: State a permutation belonging to $A$ of order (i) $4$ ; (ii) $6$ .
14N.3srg.hl.TZ0.3c: Let $P =$ {all permutations in $A$ where exactly two integers change position}, and...
14N.3srg.hl.TZ0.4a: Prove that for all $a \in G,{\text{ }}f({a^{ - 1}}) = {\left( {f(a)} \right)^{ - 1}}$ .
14N.3srg.hl.TZ0.4b: Let $\{ H,{\text{ }} \circ \}$ be the cyclic group of order seven, and let $p$ be a...
14N.3srg.hl.TZ0.5a: State Lagrange’s theorem.
14N.3srg.hl.TZ0.5d: Let $\{ H,{\rm{ }} * {\rm{\} }}$ be a subgroup of $\{ G,{\rm{ }} * {\rm{\} }}$ .Let $R$ ...
14N.3srg.hl.TZ0.5b: Verify that the inverse of $a * {b^{ - 1}}$ is equal to $b * {a^{ - 1}}$ .
14N.3srg.hl.TZ0.5e: Let $\{ H,{\rm{ }} * {\rm{\} }}$ be a subgroup of $\{ G,{\rm{ }} * {\rm{\} }}$ .Let $R$ ...

Hide related questions

Question

Markscheme

Examiners report

Syllabus sections

View options