| Date | May 2014 | Marks available | 12 | Reference code | 14M.3srg.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Determine, Find, Justify, and State | Question number | 1 | Adapted from | N/A |
Question
The binary operation \(\Delta\) is defined on the set \(S =\) {1, 2, 3, 4, 5} by the following Cayley table.
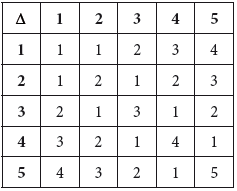
(a) State whether S is closed under the operation Δ and justify your answer.
(b) State whether Δ is commutative and justify your answer.
(c) State whether there is an identity element and justify your answer.
(d) Determine whether Δ is associative and justify your answer.
(e) Find the solutions of the equation \(a\Delta b = 4\Delta b\), for \(a \ne 4\).
Markscheme
(a) yes A1
because the Cayley table only contains elements of S R1
[2 marks]
(b) yes A1
because the Cayley table is symmetric R1
[2 marks]
(c) no A1
because there is no row (and column) with 1, 2, 3, 4, 5 R1
[2 marks]
(d) attempt to calculate \((a\Delta b)\Delta c\) and \(a\Delta (b\Delta c)\) for some \(a,{\text{ }}b,{\text{ }}c \in S\) M1
counterexample: for example, \((1\Delta 2)\Delta 3 = 2\)
\(1\Delta (2\Delta 3) = 1\) A1
Δ is not associative A1
Note: Accept a correct evaluation of \((a\Delta b)\Delta c\) and \(a\Delta (b\Delta c)\) for some \(a,{\text{ }}b,{\text{ }}c \in S\) for the M1.
[3 marks]
(e) for example, attempt to enumerate \(4\Delta b\) for b = 1, 2, 3, 4, 5 and obtain (3, 2, 1, 4, 1) (M1)
find \((a,{\text{ }}b) \in \left\{ {{\text{(2, 2), (2, 3)}}} \right\}\) for \(a \ne 4\) (or equivalent) A1A1
Note: Award M1A1A0 if extra ‘solutions’ are listed.
[3 marks]
Total [12 marks]

