| Date | May 2015 | Marks available | 2 | Reference code | 15M.3srg.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Write down | Question number | 1 | Adapted from | N/A |
Question
Consider the set \({S_3} = \{ {\text{ }}p,{\text{ }}q,{\text{ }}r,{\text{ }}s,{\text{ }}t,{\text{ }}u\} \) of permutations of the elements of the set \(\{ 1,{\text{ }}2,{\text{ }}3\} \), defined by
\(p = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 1&2&3 \end{array}} \right),{\text{ }}q = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 1&3&2 \end{array}} \right),{\text{ }}r = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 3&2&1 \end{array}} \right),{\text{ }}s = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 2&1&3 \end{array}} \right),{\text{ }}t = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 2&3&1 \end{array}} \right),{\text{ }}u = \left( {\begin{array}{*{20}{c}} 1&2&3 \\ 3&1&2 \end{array}} \right).\)
Let \( \circ \) denote composition of permutations, so \(a \circ b\) means \(b\) followed by \(a\). You may assume that \(({S_3},{\text{ }} \circ )\) forms a group.
Complete the following Cayley table
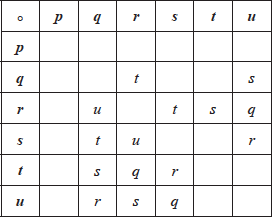
[5 marks]
(i) State the inverse of each element.
(ii) Determine the order of each element.
Write down the subgroups containing
(i) \(r\),
(ii) \(u\).
Markscheme
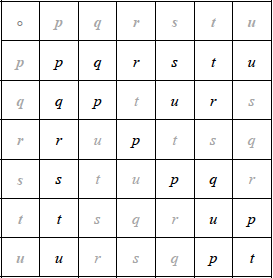(M1)A4
Note: Award M1 for use of Latin square property and/or attempted multiplication, A1 for the first row or column, A1 for the squares of \(q\), \(r\) and \(s\), then A2 for all correct.
(i) \({p^{ - 1}} = p,{\text{ }}{q^{ - 1}} = q,{\text{ }}{r^{ - 1}} = r,{\text{ }}{s^{ - 1}} = s\) A1
\({t^{ - 1}} = u,{\text{ }}{u^{ - 1}} = t\) A1
Note: Allow FT from part (a) unless the working becomes simpler.
(ii) using the table or direct multiplication (M1)
the orders of \(\{ p,{\text{ }}q,{\text{ }}r,{\text{ }}s,{\text{ }}t,{\text{ }}u\} \) are \(\{ 1,{\text{ }}2,{\text{ }}2,{\text{ }}2,{\text{ }}3,{\text{ }}3\} \) A3
Note: Award A1 for two, three or four correct, A2 for five correct.
[6 marks]
(i) \(\{ p,{\text{ }}r\} {\text{ }}\left( {{\text{and }}({S_3},{\text{ }} \circ )} \right)\) A1
(ii) \(\{ p,{\text{ }}u,{\text{ }}t\} {\text{ }}\left( {{\text{and }}({S_3},{\text{ }} \circ )} \right)\) A1
Note: Award A0A1 if the identity has been omitted.
Award A0 in (i) or (ii) if an extra incorrect “subgroup” has been included.
[2 marks]
Total [13 marks]
Examiners report
The majority of candidates were able to complete the Cayley table correctly. Unfortunately, many wasted time and space, laboriously working out the missing entries in the table - the identity is \(p\) and the elements \(q\), \(r\) and \(s\) are clearly of order two, so 14 entries can be filled in without any calculation. A few candidates thought \(t\) and \(u\) had order two.
Generally well done. A few candidates were unaware of the definition of the order of an element.
Often well done. A few candidates stated extra, and therefore incorrect subgroups.
