| Date | November 2017 | Marks available | 2 | Reference code | 17N.3srg.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Describe | Question number | 2 | Adapted from | N/A |
Question
\(A\), \(B\) and \(C\) are three subsets of a universal set.
Consider the sets \(P = \{ 1,{\text{ }}2,{\text{ }}3\} ,{\text{ }}Q = \{ 2,{\text{ }}3,{\text{ }}4\} \) and \(R = \{ 1,{\text{ }}3,{\text{ }}5\} \).
Represent the following set on a Venn diagram,
\(A\Delta B\), the symmetric difference of the sets \(A\) and \(B\);
Represent the following set on a Venn diagram,
\(A \cap (B \cup C)\).
For sets \(P\), \(Q\) and \(R\), verify that \(P \cup (Q\Delta R) \ne (P \cup Q)\Delta (P \cup R)\).
In the context of the distributive law, describe what the result in part (b)(i) illustrates.
Markscheme
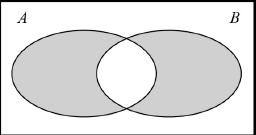 A1
A1
[1 mark]
Note: Accept alternative set configurations
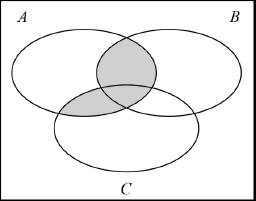 A1
A1
Note: Accept alternative set configurations.
[1 mark]
LHS:
\(Q\Delta R = \{ 1,{\text{ }}2,{\text{ }}4,{\text{ }}5\} \) (A1)
\(P \cup (Q\Delta R) = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\} \) A1
RHS:
\(P \cup Q = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4\} \) and \(P \cup R = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}5\} \) (A1)
\((P \cup Q)\Delta (P \cup R) = \{ 4,{\text{ }}5\} \) A1
hence \(P \cup (Q\Delta R) \ne (P \cup Q)\Delta (P \cup R)\) AG
[4 marks]
the result shows that union is not distributive over symmetric difference A1R1
Notes: Award A1 for “union is not distributive” and R1 for “over symmetric difference”. Condone use of \( \cup \) and \(\Delta \).
[2 marks]

