| Date | November 2015 | Marks available | 4 | Reference code | 15N.3srg.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The binary operation \( * \) is defined on the set \(T = \{ 0,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \) by \(a * b = (a + b - ab)(\bmod 7),{\text{ }}a,{\text{ }}b \in T\).
Copy and complete the following Cayley table for \(\{ T,{\text{ }} * \} \).
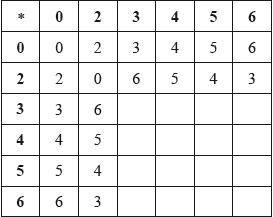
Prove that \(\{ T,{\text{ }} * \} \) forms an Abelian group.
Find the order of each element in \(T\).
Given that \(\{ H,{\text{ }} * \} \) is the subgroup of \(\{ T,{\text{ }} * \} \) of order \(2\), partition \(T\) into the left cosets with respect to \(H\).
Markscheme
Cayley table is
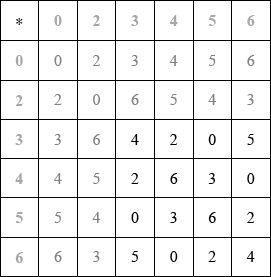 A4
A4
award A4 for all 16 correct, A3 for up to 2 errors, A2 for up to 4 errors, A1 for up to 6 errors
[4 marks]
closed as no other element appears in the Cayley table A1
symmetrical about the leading diagonal so commutative R1
hence it is Abelian
\(0\) is the identity
as \(x * 0( = 0 * x) = x + 0 - 0 = x\) A1
\(0\) and \(2\) are self inverse, \(3\) and \(5\) is an inverse pair, \(4\) and \(6\) is an inverse pair A1
Note: Accept “Every row and every column has a \(0\) so each element has an inverse”.
\((a * b) * c = (a + b - ab) * c = a + b - ab + c - (a + b - ab)c\) M1
\( = a + b + c - ab - ac - bc + abc\) A1
\(a * (b * c) = a * (b + c - bc) = a + b + c - bc - a(b + c - bc)\) A1
\( = a + b + c - ab - ac - bc + abc\)
so \((a * b) * c = a * (b * c)\) and \( * \) is associative
Note: Inclusion of mod 7 may be included at any stage.
[7 marks]
\(0\) has order \(1\) and \(2\) has order \(2\) A1
\({3^2} = 4,{\text{ }}{3^3} = 2,{\text{ }}{3^4} = 6,{\text{ }}{3^5} = 5,{\text{ }}{3^6} = 0\) so \(3\) has order \(6\) A1
\({4^2} = 6,{\text{ }}{4^3} = 0\) so \(4\) has order \(3\) A1
\(5\) has order \(6\) and \(6\) has order \(3\) A1
[4 marks]
\(H = \{ 0,{\text{ }}2\} \) A1
\(0 * \{ 0,{\text{ }}2\} = \{ 0,{\text{ }}2\} ,{\text{ }}2 * \{ 0,{\text{ }}2\} = \{ 2,{\text{ }}0\} ,{\text{ }}3 * \{ 0,{\text{ }}2\} = \{ 3,{\text{ }}6\} ,{\text{ }}4 * \{ 0,{\text{ }}2\} = \{ 4,{\text{ }}5\} ,\)
\(5 * \{ 0,{\text{ }}2\} = \{ 5,{\text{ }}4\} ,{\text{ }}6 * \{ 0,{\text{ }}2\} = \{ 6,{\text{ }}3\} \) M1
Note: Award the M1 if sufficient examples are used to find at least two of the cosets.
so the left cosets are \(\{ 0,{\text{ }}2\} ,{\text{ }}\{ 3,{\text{ }}6\} ,{\text{ }}\{ 4,{\text{ }}5\} \) A1
[3 marks]
Total [18 marks]
Examiners report

