| Date | November 2013 | Marks available | 14 | Reference code | 13N.3srg.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Determine, Find, Justify, and Show that | Question number | 1 | Adapted from | N/A |
Question
Consider the following functions
\(f:\left] {1,{\text{ }} + \infty } \right[ \to {\mathbb{R}^ + }\) where \(f(x) = (x - 1)(x + 2)\)
\(g:\mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) where \(g(x,{\text{ }}y) = \left( {\sin (x + y),{\text{ }}x + y} \right)\)
\(h:\mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) where \(h(x,{\text{ }}y) = (x + 3y,{\text{ }}2x + y)\)
(a) Show that \(f\) is bijective.
(b) Determine, with reasons, whether
(i) \(g\) is injective;
(ii) \(g\) is surjective.
(c) Find an expression for \({h^{ - 1}}(x,{\text{ }}y)\) and hence justify that \(h\) has an inverse function.
Markscheme
(a) Method 1
sketch of the graph of \(f\) (M1)
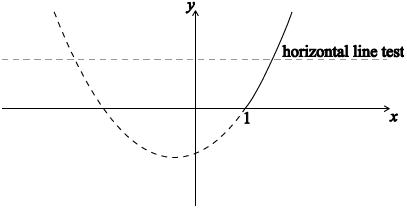
range of \(f = \) co-domain, therefore \(f\) is surjective R1
graph of \(f\) passes the horizontal line test, therefore \(f\) is injective R1
therefore \(f\) is bijective AG
Note: Other explanations may be given (eg use of derivative or description of parabola).
Method 2
Injective: \(f(a) = f(b) \Rightarrow a = b\) M1
\((a - 1)(a + 2) = (b - 1)(b + 2)\)
\({a^2} + a = {b^2} + b\)
solving for \(a\) by completing the square, or the quadratic formula, A1
\(a = b\)
surjective: for all \(y \in {\mathbb{R}^ + }\) there exists \(x \in \left] {1,{\text{ }}\infty } \right[\) such that \(f(x) = y\)
solving \(y = {x^2} + x - 2\) for x, \(x = \frac{{\sqrt {4y + 9} - 1}}{2}\). For all positive real \(y\), the minimum value for \(\sqrt {4y + 9} \) is \(3\). Hence, \(x \geqslant 1\) R1
since \(f\) is both injective and surjective, \(f\) is bijective. AG
Method 3
\(f\) is bijective if and only if \(f\) has an inverse (M1)
solving \(y = {x^2} + x - 2\) for \(x,{\text{ }}x = \frac{{\sqrt {4y + 9} - 1}}{2}\). For all positive real \(y\), the minimum value for \(\sqrt {4y + 9} \) is \(3\). Hence, \(x \geqslant 1\) R1
\({f^{ - 1}}(x) = \frac{{\sqrt {4x + 9} - 1}}{2}\) R1
\(f\) has an inverse, hence \(f\) is bijective AG
[3 marks]
(b) (i) attempt to find counterexample (M1)
eg \(g(x,{\text{ }}y) = g(y,{\text{ }}x),{\text{ }}x \ne y\) A1
g is not injective R1
(ii) \( - 1 \leqslant \sin (x + y) \leqslant 1\) (M1)
range of \(g\) is \(\left[ { - 1,{\text{ 1}}} \right] \times \mathbb{R} \ne \mathbb{R} \times \mathbb{R}\) A1
\(g\) is not surjective R1
[6 marks]
(c) let \(h(x,{\text{ }}y) = (u,{\text{ }}v)\)
then \(u = x + 3y\)
\(v = 2x + y\) (M1)
solving simultaneous equations (M1)
eg \(\left( \begin{array}{l}x\\y\end{array} \right) = {\left( {\begin{array}{*{20}{c}}1&3\\2&1\end{array}} \right)^{ - 1}}\left( \begin{array}{l}u\\v\end{array} \right) \Rightarrow \left( \begin{array}{l}x\\y\end{array} \right) = - \frac{1}{5}\left( {\begin{array}{*{20}{c}}1&{ - 3}\\{ - 2}&1\end{array}} \right)\left( \begin{array}{l}u\\v\end{array} \right)\)
\(x = \frac{{ - u + 3v}}{5}y = \frac{{2u - v}}{5}\) A1
hence \({h^{ - 1}}(x,{\text{ }}y) = \left( {\frac{{ - x + 3y}}{5},{\text{ }}\frac{{2x - y}}{5}} \right)\) A1
as this expression is defined for any values of \((x,{\text{ }}y) \in \mathbb{R} \times \mathbb{R}\) R1
the inverse of \(h\) exists AG
[5 marks]
Examiners report
For part (a), given the command term ‘show that’ and the number of marks for this part, the best approach is a graphical one, i.e., an informal approach. Many candidates chose an algebraic approach and generally made correct statements for injective and surjective. However, they often did not follow through with the necessary algebraic manipulation to make a valid conclusion. In part (b), many candidates were not able to provide valid counter-examples. In part (c) It was obvious that quite a few candidates had not seen this type of function before. Those that were able to find the inverse generally did not justify their result, and hence could not earn the final R mark.

