| Date | November 2017 | Marks available | 2 | Reference code | 17N.3srg.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | State and Justify | Question number | 1 | Adapted from | N/A |
Question
Consider the group \(\{ G,{\text{ }}{ \times _{18}}\} \) defined on the set \(\{ 1,{\text{ }}5,{\text{ }}7,{\text{ }}11,{\text{ }}13,{\text{ }}17\} \) where \({ \times _{18}}\) denotes multiplication modulo 18. The group \(\{ G,{\text{ }}{ \times _{18}}\} \) is shown in the following Cayley table.
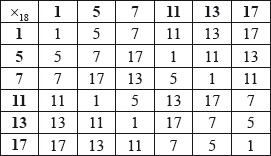
The subgroup of \(\{ G,{\text{ }}{ \times _{18}}\} \) of order two is denoted by \(\{ K,{\text{ }}{ \times _{18}}\} \).
Find the order of elements 5, 7 and 17 in \(\{ G,{\text{ }}{ \times _{18}}\} \).
State whether or not \(\{ G,{\text{ }}{ \times _{18}}\} \) is cyclic, justifying your answer.
Write down the elements in set \(K\).
Find the left cosets of \(K\) in \(\{ G,{\text{ }}{ \times _{18}}\} \).
Markscheme
considering powers of elements (M1)
5 has order 6 A1
7 has order 3 A1
17 has order 2 A1
[4 marks]
\(G\) is cyclic A1
because there is an element (are elements) of order 6 R1
Note: Accept “there is a generator”; allow A1R0.
[3 marks]
\(\{ 1,{\text{ }}17\} \) A1
[1 mark]
multiplying \(\{ 1,{\text{ }}17\} \) by each element of \(G\) (M1)
\(\{ 1,{\text{ }}17\} ,{\text{ }}\{ 5,{\text{ }}13\} ,{\text{ }}\{ 7,{\text{ }}11\} \) A1A1A1
[4 marks]

