| Date | May 2014 | Marks available | 10 | Reference code | 14M.3srg.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Show that and Find | Question number | 3 | Adapted from | N/A |
Question
Sets X and Y are defined by \({\text{ }}X = \left] {0,{\text{ }}1} \right[;{\text{ }}Y = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\} \).
(i) Sketch the set \(X \times Y\) in the Cartesian plane.
(ii) Sketch the set \(Y \times X\) in the Cartesian plane.
(iii) State \((X \times Y) \cap (Y \times X)\).
Consider the function \(f:X \times Y \to \mathbb{R}\) defined by \(f(x,{\text{ }}y) = x + y\) and the function \(g:X \times Y \to \mathbb{R}\) defined by \(g(x,{\text{ }}y) = xy\).
(i) Find the range of the function f.
(ii) Find the range of the function g.
(iii) Show that \(f\) is an injection.
(iv) Find \({f^{ - 1}}(\pi )\), expressing your answer in exact form.
(v) Find all solutions to \(g(x,{\text{ }}y) = \frac{1}{2}\).
Markscheme
(i) 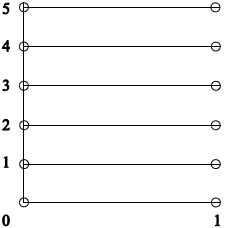
correct horizontal lines A1
correctly labelled axes A1
clear indication that the endpoints are not included A1
(ii) 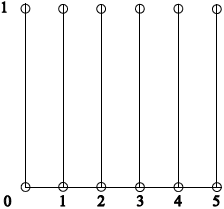
fully correct diagram A1
Note: Do not penalize the inclusion of endpoints twice.
(iii) the intersection is empty A1
[5 marks]
(i) range \((f) = \left] {0,{\text{ 1}}} \right[ \cup \left] {1,{\text{ 2}}} \right[ \cup \rm{L} \cup \left] {5,{\text{ 6}}} \right[\) A1A1
Note: A1 for six intervals and A1 for fully correct notation.
Accept \(0 < x < 6,{\text{ }}x \ne 0{\text{, 1, 2, 3, 4, 5, 6}}\).
(ii) range \((g) = \left[ {0,{\text{ 5}}} \right[\) A1
(iii) Attempt at solving
\(f({x_1},{\text{ }}{y_1}) = f({x_2},{\text{ }}{y_2})\) M1
\(f(x,{\text{ }}y) \in \left] {y,{\text{ }}y + 1} \right[ \Rightarrow {y_1} = {y_2}\) M1
and then \({x_1} = {x_2}\) A1
so \(f\) is injective AG
(iv) \({f^{ - 1}}(\pi ) = (\pi - 3,{\text{ }}3)\) A1A1
(v) solutions: (0.5, 1), (0.25, 2), \(\left( {\frac{1}{6},{\text{ 3}}} \right)\), (0.125, 4), (0.1, 5) A2
Note: A2 for all correct, A1 for 2 correct.
[10 marks]

