| Date | November 2017 | Marks available | 4 | Reference code | 17N.3srg.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Determine | Question number | 3 | Adapted from | N/A |
Question
The relation R is defined on \(\mathbb{R} \times \mathbb{R}\) such that \(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2})\) if and only if \({x_1}{y_1} = {x_2}{y_2}\).
Show that R is an equivalence relation.
Determine the equivalence class of R containing the element \((1,{\text{ }}2)\) and illustrate this graphically.
Markscheme
R is an equivalence relation if
R is reflexive, symmetric and transitive A1
\({x_1}{y_1} = {x_1}{y_1} \Rightarrow ({x_1},{\text{ }}{y_1})R({x_1},{\text{ }}{y_1})\) A1
so R is reflexive
\(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2}) \Rightarrow {x_1}{y_1} = {x_2}{y_2} \Rightarrow {x_2}{y_2} = {x_1}{y_1} \Rightarrow ({x_2},{\text{ }}{y_2})R({x_1},{\text{ }}{y_1})\) A1
so R is symmetric
\(({x_1},{\text{ }}{y_1})R({x_2},{\text{ }}{y_2})\) and \(({x_2},{\text{ }}{y_2})R({x_3},{\text{ }}{y_3}) \Rightarrow {x_1}{y_1} = {x_2}{y_2}\) and \({x_2}{y_2} = {x_3}{y_3}\) M1
\( \Rightarrow {x_1}{y_1} = {x_3}{y_3} \Rightarrow ({x_1},{\text{ }}{y_1})R({x_3},{\text{ }}{y_3})\) A1
so R is transitive
R is an equivalence relation AG
[5 marks]
\((x,{\text{ }}y)R(1,{\text{ }}2)\) (M1)
the equivalence class is \(\{ (x,{\text{ }}y)|xy = 2\} \) A1
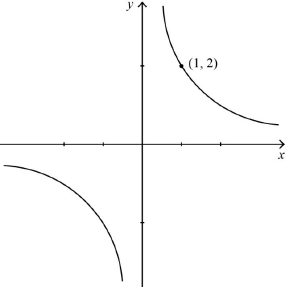
correct graph A1
\((1,{\text{ }}2)\) indicated on the graph A1
Note: Award last A1 only if plotted on a curve representing the class.
[4 marks]

