DP Mathematics: Applications and Interpretation Questionbank

Topic 1—Number and algebra
Description
[N/A]Directly related questions
-
18M.1.SL.TZ2.T_4a:
Complete the second column of the table by giving one example of a number from each set.
-
18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
-
18N.2.SL.TZ0.T_1a.iii:
Use your graphic display calculator to write down r , Pearson’s product–moment correlation coefficient.
-
18N.2.SL.TZ0.T_1c.i:
Use the regression line y on x to estimate Jerome’s examination score.
-
22M.2.AHL.TZ1.4a.iii:
Hence state the long-term velocity of the particle.
-
22M.2.AHL.TZ1.7a.i:
By considering the image of , find .
-
22M.2.AHL.TZ1.7c.ii:
Hence find the angle and direction of the rotation represented by .
-
22M.2.AHL.TZ1.7b:
Write down the matrix .
-
22M.2.SL.TZ2.2d.i:
Calculate the value of .
-
18M.2.AHL.TZ1.H_1a:
Find the first term and the common difference of the sequence.
-
19M.2.AHL.TZ2.H_7:
Suppose that is the first term of a geometric series with common ratio .
Prove, by mathematical induction, that the sum of the first terms, is given by
, where .
-
22M.2.AHL.TZ2.5b:
Find the eigenvalues of .
-
22M.2.AHL.TZ2.5c:
Find the eigenvectors of .
-
18M.1.AHL.TZ1.H_11a.ii:
Sketch on an Argand diagram the points represented by w0 , w1 , w2 and w3.
-
22M.1.AHL.TZ1.10b.ii:
For this value of , plot the approximate position of on the Argand diagram.
-
22M.1.AHL.TZ1.10a.ii:
.
-
22M.1.AHL.TZ1.10b.i:
Find this value of .
-
22M.1.AHL.TZ1.11a:
Find an eigenvector corresponding to the eigenvalue of . Give your answer in the form , where .
-
22M.1.AHL.TZ1.12b:
Find the value of .
-
22M.1.AHL.TZ2.13b:
Hence write down the maximum voltage in the circuit.
-
22M.1.AHL.TZ2.15b:
Find the value of .
-
EXM.2.SL.TZ0.1b.i:
the amount Paul pays each month.
-
22M.2.SL.TZ1.2c.ii:
Find the value of for this path.
-
22M.2.SL.TZ1.2b.ii:
.
-
22M.2.SL.TZ1.2c.i:
Show that Eddie needs tiles.
-
EXM.2.SL.TZ0.2a.i:
Calculate the monthly repayment using option 1.
-
EXM.2.SL.TZ0.2c.ii:
option 2.
-
SPM.2.SL.TZ0.1a.i:
Find the repayment made each quarter.
-
EXM.1.AHL.TZ0.26b:
Calculate det (BA).
-
18M.2.AHL.TZ1.H_1b:
Calculate the number of positive terms in the sequence.
-
EXM.3.AHL.TZ0.5g:
State geometrically what transformation the matrix represents.
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
18M.1.SL.TZ1.T_7a.ii:
For that day find the weight of Sergei’s first lift.
-
EXM.2.SL.TZ0.2a.ii:
Calculate the total amount Sophie would pay, using option 1.
-
SPM.1.AHL.TZ0.15a.ii:
draw , , , and on the following Argand diagram.
-
EXM.2.SL.TZ0.2b.i:
Calculate the number of months it will take to repay the mortgage using option 2.
-
17M.2.SL.TZ1.T_1b.ii:
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
-
16N.1.AHL.TZ0.H_6a:
Write down the value of .
-
18M.2.SL.TZ1.T_3b:
Calculate 14 000 USD in INR.
-
SPM.1.SL.TZ0.2b:
Calculate the price of a ticket in the 16th row.
-
EXM.1.AHL.TZ0.6a:
Find Q.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
17M.1.SL.TZ2.T_6a:
Write down the median length of these leaves.
-
22M.2.SL.TZ1.2a.ii:
.
-
22M.2.SL.TZ1.2b.i:
.
-
22M.2.SL.TZ2.2a.ii:
remaining in the bag at the end of the first day.
-
EXM.2.AHL.TZ0.23a:
Find the values of for which the matrix (A − I) is singular.
-
16N.1.SL.TZ0.S_9d:
Show that .
-
18N.2.SL.TZ0.T_1b.i:
Find the exact value of m and of c for these data.
-
21M.1.AHL.TZ2.12a.i:
Find the value of .
-
EXM.1.AHL.TZ0.7b:
Let .
Find the value of .
-
18M.1.AHL.TZ2.H_5a:
Show that A is an arithmetic sequence, stating its common difference d in terms of r.
-
EXN.3.AHL.TZ0.2d.i:
state the coordinates, , of its image in .
-
22M.1.SL.TZ1.13c:
Find the total vertical distance travelled by the ball from the point at which it is dropped until the fourth bounce.
-
22M.1.AHL.TZ1.10a.iii:
.
-
22M.1.AHL.TZ1.12c:
Find the average number of earthquakes in a year with a magnitude of at least .
-
SPM.2.AHL.TZ0.3a.ii:
Find the total amount paid for the car.
-
22M.1.AHL.TZ2.8b:
Find the upper bound and lower bound of the area of the sector.
-
22M.1.AHL.TZ2.8c:
Find, with justification, the largest possible percentage error if the answer to part (a) is recorded as the area of the sector.
-
22M.2.SL.TZ1.1e:
Calculate the percentage error in the maximum number of daylight hours Boris recorded in the diagram.
-
22M.2.SL.TZ1.2d:
Find the total area of the tiles in Eddie’s path. Give your answer in the form where and is an integer.
-
22M.2.AHL.TZ1.4a.ii:
Find the eigenvalues for the matrix .
-
22M.2.AHL.TZ1.7a.ii:
By considering the image of and , show that
.
-
22M.2.AHL.TZ1.7d.ii:
Find the value of and the value of .
-
22M.2.SL.TZ2.2b:
Calculate the number of days that Scott can feed his dog with one bag of food.
-
22M.2.SL.TZ2.2c:
Determine the amount that Scott expects to spend on dog food in . Round your answer to the nearest dollar.
-
22M.2.SL.TZ2.2d.ii:
Describe what the value in part (d)(i) represents in this context.
-
22M.2.AHL.TZ2.4c:
(i) the gradient of this line in terms of ;
(ii) the -intercept of this line in terms of .
-
22M.2.AHL.TZ2.4d:
Find the equation of the regression line for on .
-
22M.2.AHL.TZ2.7b:
Find the eigenvalues of the system of coupled first order equations given in part (a).
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
EXN.1.SL.TZ0.5b.i:
Write an expression for in terms of .
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
EXM.2.AHL.TZ0.4:
The matrices A, B, X are given by
A = , B = , X = , , , , .
Given that AX + X = Β, find the exact values of , , and .
-
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of .
Find the total number of slices Mia can cut from this pie.
-
17N.1.SL.TZ0.S_2b:
Find the tenth term.
-
17M.2.SL.TZ1.T_1d:
Use your regression line to estimate the average weight of the brain of grey wolves.
-
21M.1.AHL.TZ1.9b:
Describe these two transformations and give the order in which they are applied.
-
EXM.2.AHL.TZ0.8d.i:
Write down these three equations as a matrix equation.
-
EXN.2.AHL.TZ0.5a.i:
the eigenvalues.
-
21N.2.AHL.TZ0.4b:
Three drones are initially positioned at the points , and . After performing the movements listed above, the drones are positioned at points , and respectively.
Show that the area of triangle is equal to the area of triangle .
-
21N.2.AHL.TZ0.6a:
Given that , show that .
-
22M.1.SL.TZ1.13a:
Show that the maximum height reached by the ball after it has bounced for the sixth time is , to the nearest .
-
22M.1.SL.TZ1.5a:
Write down three equations that express the information given above.
-
21N.2.SL.TZ0.2f:
State whether, for all , the university will have places available for all applicants. Justify your answer.
-
21N.2.AHL.TZ0.4a.iii:
Find .
-
EXN.2.AHL.TZ0.5d:
Write down a condition on the size of the initial population of if it is to avoid its population reducing to zero.
-
EXN.2.AHL.TZ0.5e.i:
Find the value of at which .
-
EXN.3.AHL.TZ0.2f.ii:
Write down .
-
EXN.1.AHL.TZ0.14b:
An equilateral triangle is to be drawn on the Argand plane with one of the vertices at the point corresponding to and all the vertices equidistant from .
Find the points that correspond to the other two vertices. Give your answers in Cartesian form.
-
22M.2.SL.TZ2.2a.i:
fed to the dog per day.
-
22M.1.SL.TZ2.13b:
For option 2, find the minimum value of that Juliana would need to invest each year. Give your answer to the nearest dollar.
-
22M.1.SL.TZ2.13a:
For option 1, determine the minimum amount Juliana would need to invest. Give your answer to the nearest dollar.
-
22M.1.SL.TZ2.4a:
Calculate the pH of the coffee.
-
22M.1.SL.TZ2.4b:
Determine whether the unknown liquid is more or less acidic than the coffee. Justify your answer mathematically.
-
22M.1.AHL.TZ2.13a:
Find an expression for in the form , where and are real constants.
-
22M.1.AHL.TZ2.7:
The sum of an infinite geometric sequence is .
The first term is more than the second term.
Find the third term. Justify your answer.
-
21N.1.SL.TZ0.10b.i:
Find the amount Raul and Rosy will still owe the bank at the end of the first years.
-
21N.1.AHL.TZ0.6b:
Find the least value of such that .
-
21N.2.AHL.TZ0.4c:
Find a single transformation that is equivalent to the three transformations represented by matrix .
-
21N.2.AHL.TZ0.5c.i:
Find the maximum value of .
-
21N.2.AHL.TZ0.6c.i:
Find the eigenvalues of matrix .
-
22M.1.SL.TZ1.11a:
Find the value of .
-
22M.1.SL.TZ1.11b:
Find the value of .
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.SL.TZ1.13b:
Find the number of times, after the first bounce, that the maximum height reached is greater than .
-
22M.1.SL.TZ1.5b:
Find the number of each type of ticket sold.
-
22M.2.SL.TZ1.2a.i:
.
-
22M.1.AHL.TZ1.10a.i:
.
-
22M.2.AHL.TZ1.7d.i:
Write down an equation satisfied by .
-
22M.1.AHL.TZ1.12a:
Find the value of .
-
22M.2.AHL.TZ1.7c.i:
Use to find the matrix .
-
22M.2.AHL.TZ1.4a.i:
Use the substitution to show that this equation can be written as
.
-
21N.2.SL.TZ0.2b.i:
Write down the common ratio of the sequence.
-
21N.2.AHL.TZ0.4a.i:
Write down each of the transformations in matrix form, clearly stating which matrix represents each transformation.
-
21N.2.AHL.TZ0.4a.ii:
Find a single matrix that defines a transformation that represents the overall change in position.
-
21N.2.AHL.TZ0.4a.iv:
Hence state what the value of indicates for the possible movement of the drone.
-
21N.2.AHL.TZ0.5b.ii:
Hence find in the form , where and .
-
21N.2.AHL.TZ0.5b.i:
Find in the form .
-
21N.2.AHL.TZ0.6c.ii:
Find the eigenvectors of matrix .
- 957233: This is an example question for the example test. You can delete this question.
-
EXM.1.AHL.TZ0.30c:
Find the matrix X, such that AX = C.
-
18N.2.SL.TZ0.T_1a.ii:
Use your graphic display calculator to write down , the mean examination score.
-
17M.1.AHL.TZ2.H_3b:
the value of ;
-
19M.2.AHL.TZ1.H_6a:
Show the points represented by and on the following Argand diagram.
-
EXM.3.AHL.TZ0.5i:
Write down the equations of two lines of symmetry for the curve in and in part (b).
-
17N.2.AHL.TZ0.H_12c:
Given that Phil’s aim is to own the house after 20 years, find the value for to the nearest dollar.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.1.SL.TZ0.S_9b:
Show that the sum of the infinite sequence is .
-
EXM.2.AHL.TZ0.8a:
Write down the value of .
-
EXM.1.AHL.TZ0.27a:
(A + B)2 = A2 + 2AB + B2
-
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
-
EXM.2.AHL.TZ0.23b.iii:
Use the result from part (b) (ii) to explain why A is non-singular.
-
19M.1.AHL.TZ2.H_1:
In an arithmetic sequence, the sum of the 3rd and 8th terms is 1.
Given that the sum of the first seven terms is 35, determine the first term and the common difference.
-
EXM.2.AHL.TZ0.10c:
Hence find A−1B.
-
EXM.3.AHL.TZ0.5h.i:
the curve in and in part (e) (ii), giving a reason.
-
EXM.1.AHL.TZ0.27c:
CA = B C =
-
EXM.1.AHL.TZ0.34:
The square matrix X is such that X3 = 0. Show that the inverse of the matrix (I – X) is I + X + X2.
-
EXM.2.SL.TZ0.1c.i:
option 1.
-
18M.2.SL.TZ2.T_4c:
Find the tea-shop’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4e:
In the mth week the tea-shop’s total profit exceeds the café’s total profit, for the first time since they both opened.
Find the value of m.
-
17M.1.SL.TZ2.T_6b:
Write down the number of leaves with a length less than or equal to 8 cm.
-
EXM.2.SL.TZ0.2d.i:
Use your answer to part (a)(i) to calculate the amount remaining on her mortgage after the first 10 years.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
EXM.2.SL.TZ0.1b.ii:
the total amount that Paul has to pay.
-
18M.1.AHL.TZ0.F_2a:
Show that A4 = 12A + 5I.
-
17M.1.AHL.TZ1.H_7b:
determine the value of .
-
17M.1.SL.TZ2.T_5b:
Find the total number of sticks used by Tomás for all 24 diagrams.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
18M.1.SL.TZ2.T_4b:
Josh states: “Every integer is a natural number”.
Write down whether Josh’s statement is correct. Justify your answer.
-
SPM.1.AHL.TZ0.15a.i:
find the values of , , and .
-
16N.2.AHL.TZ0.H_12a:
Find an expression for and show that .
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
18M.1.SL.TZ1.T_7a.i:
For that day find how much weight was added after each lift.
-
EXM.3.AHL.TZ0.5d.i:
Find matrix R.
-
EXM.1.AHL.TZ0.7a.ii:
Find the value of .
-
19M.2.SL.TZ2.T_4d.iii:
Hence find the total amount of antibiotic, in mg, that Ted receives during the first days.
-
EXM.2.SL.TZ0.1a.ii:
the total amount that Paul has to pay.
-
17M.2.SL.TZ1.T_1a:
Find the range of the average body weights for these seven species of mammal.
-
19M.2.SL.TZ2.T_4b:
Write down the value of and the value of .
-
17M.1.SL.TZ2.T_9a:
Write down the common ratio of the sequence.
-
19M.2.AHL.TZ0.F_3a:
Given that M3 can be written as a quadratic expression in M in the form aM2 + bM + cI , determine the values of the constants a, b and c.
-
19M.2.AHL.TZ0.F_3d:
Find a quadratic expression in M for the inverse matrix M–1.
-
19N.1.SL.TZ0.T_8a:
Calculate the value of Siân’s investment after four years. Give your answer correct to two decimal places.
-
EXM.2.AHL.TZ0.6a:
Write down A−1.
-
EXM.2.AHL.TZ0.6b:
Find D.
-
EXM.2.AHL.TZ0.7c.ii:
Find T4.
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
EXM.1.AHL.TZ0.45b.i:
Find the matrix DA.
-
EXM.1.AHL.TZ0.8a:
Write down the inverse matrix A−1.
-
EXM.2.AHL.TZ0.7d:
Using your results from part (a) (ii), find T100.
-
SPM.2.SL.TZ0.1a.iii:
Find the interest paid on the loan.
-
17M.2.SL.TZ1.T_1b.i:
For the data from these seven species calculate , the Pearson’s product–moment correlation coefficient;
-
16N.1.SL.TZ0.S_9a:
Find .
-
EXM.1.AHL.TZ0.9a.ii:
Write down the value of .
-
EXM.2.AHL.TZ0.5b:
find AB.
-
EXM.2.AHL.TZ0.7a.i:
Find 4.
-
EXM.1.AHL.TZ0.9a.i:
Write down the value of .
-
EXM.2.AHL.TZ0.5a:
write down A + B.
-
EXM.1.AHL.TZ0.9b:
Write these equations as a matrix equation.
-
EXM.1.AHL.TZ0.8b.i:
Express X in terms of A−1 and B.
-
EXM.2.AHL.TZ0.11b:
Write down M−1.
-
EXM.2.AHL.TZ0.11a:
Write down the determinant of M.
-
SPM.2.SL.TZ0.1b.i:
Find the amount to be borrowed for this option.
-
SPM.2.SL.TZ0.1a.ii:
Find the total amount paid for the car.
-
SPM.2.AHL.TZ0.3a.iii:
Find the interest paid on the loan.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
EXM.2.AHL.TZ0.20c.ii:
A–1 = I – A.
-
EXM.1.AHL.TZ0.54a:
Find det A.
-
19N.1.SL.TZ0.T_7a:
Find the common ratio.
-
EXM.1.AHL.TZ0.27b:
(A – kI)3 = A3 – 3kA2 + 3k2A – k3
-
EXM.2.AHL.TZ0.8b:
Show that .
-
EXM.2.AHL.TZ0.3c:
Using this value of , find and hence solve the system of equations:
-
EXM.2.AHL.TZ0.20c.i:
A3 = –I.
-
EXM.2.AHL.TZ0.6c:
Find X.
-
SPM.2.AHL.TZ0.3a.i:
Find the repayment made each quarter.
-
EXM.2.AHL.TZ0.20a.ii:
Show that .
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
EXM.1.AHL.TZ0.11a:
Find A + B.
-
EXM.1.SL.TZ0.1a:
Calculate the value of her savings after 10 years.
-
EXM.2.AHL.TZ0.7b.i:
Find M2.
-
EXM.1.AHL.TZ0.16b.ii:
Write down for this value of .
-
EXM.1.AHL.TZ0.4b.i:
Given that XA + B = C, express X in terms of A–1, B and C.
-
18M.2.SL.TZ1.S_7a:
Given that xk + 1 = xk + a, find a.
-
SPM.1.AHL.TZ0.18:
The rate, , of a chemical reaction at a fixed temperature is related to the concentration of two compounds, and , by the equation
, where , , .
A scientist measures the three variables three times during the reaction and obtains the following values.
Find , and .
-
SPM.2.SL.TZ0.1b.ii:
Find the annual interest rate, .
-
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
-
EXM.1.AHL.TZ0.46:
If A = and B = , find 2 values of and , given that AB = BA.
-
EXM.2.AHL.TZ0.20a.iii:
Hence find the value of .
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
-
EXM.2.AHL.TZ0.3a:
Find in terms of .
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
EXM.1.AHL.TZ0.45b.ii:
Find B if AB = C.
-
EXM.1.AHL.TZ0.42:
Given the matrix A = find the values of the real number for which where
-
EXM.2.AHL.TZ0.22c:
If all of the elements of M are positive, find the range of possible values for .
-
18M.1.AHL.TZ1.H_11a.i:
Express w2 and w3 in modulus-argument form.
-
21M.2.SL.TZ1.3b:
Find the minimum value of , where .
-
EXM.2.SL.TZ0.2c.i:
option 1.
-
18M.2.SL.TZ1.T_3d:
Harinder chose option B. At the end of five years, Harinder converted this investment back to USD. The exchange rate, at that time, was 1 USD = 67.16 INR.
Calculate how much more money, in USD, Harinder earned by choosing option B instead of option A.
-
21M.2.AHL.TZ1.5a:
It is sunny today. Find the probability that it will be sunny in three days’ time.
-
21M.2.AHL.TZ1.5b:
Find the eigenvalues and eigenvectors of .
-
21M.2.AHL.TZ1.5c.ii:
Write down the matrix .
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
19M.2.AHL.TZ0.F_3b:
Show that M4 = 19M2 + 40M + 30I.
-
SPM.1.SL.TZ0.2a:
Write down the value of the common difference,
-
18M.2.SL.TZ2.S_4a:
Find the common ratio.
-
EXM.1.AHL.TZ0.9c:
Solve the matrix equation.
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
EXM.1.AHL.TZ0.16a:
Find a relationship between and if the matrices and commute under matrix multiplication.
-
17N.1.SL.TZ0.S_2c:
Find the sum of the first ten terms.
-
19M.1.AHL.TZ0.F_13b:
It is now given that A is singular.
By considering appropriate determinants, prove that f is not a bijection.
-
EXM.1.AHL.TZ0.3:
and are 2 × 2 matrices, where and . Find
-
EXM.3.AHL.TZ0.5h.ii:
the curve in and in part (b).
-
EXM.1.AHL.TZ0.29b:
Calculate M2.
-
16N.1.AHL.TZ0.H_6b:
Find the value of .
-
EXM.1.AHL.TZ0.7a.i:
Write down the value of .
-
17N.2.AHL.TZ0.H_12d.ii:
Hence or otherwise, find the minimum value of that would permit David to withdraw annual amounts of $5000 indefinitely. Give your answer to the nearest dollar.
-
19M.1.AHL.TZ0.F_13a:
Given that A is non-singular, prove that f is a bijection.
-
EXM.2.AHL.TZ0.21a.ii:
does X–1 + Y–1 have an inverse? Justify your conclusion.
-
EXM.3.AHL.TZ0.5f:
Find the Cartesian equation satisfied by and and state the geometric shape that this curve represents.
-
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
-
20N.1.SL.TZ0.T_8a:
Calculate the value of Imon’s investment after years.
-
18N.1.AHL.TZ0.H_4a:
Find the value of for which the system of equations does not have a unique solution.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
EXM.2.AHL.TZ0.9b:
Hence or otherwise solve
-
EXM.2.AHL.TZ0.8e:
The function can also be written where and are integers. Find and .
-
EXM.1.AHL.TZ0.16b.i:
Find the value of if the determinant of matrix is −1.
-
18M.1.AHL.TZ2.H_11c:
The region R, is bounded by the graph of the function found in part (b), the x-axis, and the lines and where . The area of R is .
Find the value of .
-
EXM.2.AHL.TZ0.21a.i:
find X and Y.
-
17M.1.AHL.TZ1.H_7a:
find the value of .
-
EXM.2.AHL.TZ0.7b.ii:
Show that M3 = .
-
EXM.1.AHL.TZ0.31:
Find the determinant of A, where A = .
-
19M.1.AHL.TZ0.F_3a.i:
Show that the eigenvalues of A are real if .
-
19M.1.AHL.TZ0.F_3b.i:
Determine the eigenvalues of B.
-
17M.1.SL.TZ1.T_5b:
The company also makes a ladder that is 1050 cm long.
Find the maximum number of rungs in this 1050 cm long ladder.
-
16N.1.AHL.TZ0.H_6c:
Prove that is an arithmetic sequence, stating clearly its common difference.
-
EXM.2.AHL.TZ0.7c.i:
Write down M4.
-
18N.2.SL.TZ0.S_5:
The sum of an infinite geometric sequence is 33.25. The second term of the sequence is 7.98. Find the possible values of .
-
EXM.1.AHL.TZ0.35b:
Hence, find the point of intersection of the three planes.
-
EXM.2.AHL.TZ0.21b.ii:
and hence find an expression for .
-
17N.2.AHL.TZ0.H_1:
Boxes of mixed fruit are on sale at a local supermarket.
Box A contains 2 bananas, 3 kiwifruit and 4 melons, and costs $6.58.
Box B contains 5 bananas, 2 kiwifruit and 8 melons and costs $12.32.
Box C contains 5 bananas and 4 kiwifruit and costs $3.00.
Find the cost of each type of fruit.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
18N.1.AHL.TZ0.H_4b:
Find the solution of the system of equations when .
-
19N.2.SL.TZ0.T_3b:
Show that the total number of triangular panes, , in the first levels is given by:
.
-
17N.1.SL.TZ0.S_2a:
Find the common difference.
-
EXM.1.AHL.TZ0.28:
Consider the matrix A , where .
Find the value of for which A is singular.
-
EXM.2.AHL.TZ0.11c:
Hence solve M.
-
EXM.2.SL.TZ0.2b.ii:
Calculate the total amount Sophie would pay, using option 2.
-
EXM.2.AHL.TZ0.9a:
Write down the inverse of the matrix A = .
-
EXM.3.AHL.TZ0.5a:
Find the eigenvalues for . For each eigenvalue find the set of associated eigenvectors.
-
EXM.1.AHL.TZ0.8b.ii:
Hence, solve for X.
-
18M.1.AHL.TZ1.H_5:
Solve .
-
EXM.2.SL.TZ0.2d.ii:
Hence calculate her monthly repayment for the final 10 years.
-
EXM.3.AHL.TZ0.5b:
Show that the matrix equation is equivalent to the Cartesian equation .
-
EXM.3.AHL.TZ0.5c.i:
Show that and are unit eigenvectors and that they correspond to different eigenvalues.
-
19M.2.SL.TZ2.T_4a.i:
Write down an equation, in terms of and , for the amount of the drug that she receives on the seventh day.
-
EXM.1.AHL.TZ0.29a:
Show that M is non-singular.
-
17M.1.AHL.TZ1.H_2a.ii:
By expressing and in modulus-argument form write down the argument of .
-
18N.1.SL.TZ0.S_3a:
Find u8.
-
EXM.2.AHL.TZ0.10b:
Given that 2A + B = , find the value of and of .
-
EXM.2.AHL.TZ0.23c:
Use the values from part (b) (i) to express A4 in the form A+ I where , .
-
SPM.2.AHL.TZ0.3b.i:
Find the amount to be borrowed for this option.
-
EXM.1.SL.TZ0.6a:
Calculate the amount Yejin needs to have saved into her annuity fund, in order to meet her retirement goal.
-
EXN.3.AHL.TZ0.2g:
Find the value of at which the enlargement scale factor equals zero.
-
EXM.1.AHL.TZ0.54b:
Find the set of values of for which the system has a unique solution.
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.1.SL.TZ0.S_9e:
Given that is equal to half the sum of the infinite geometric sequence, find , giving your answer in the form , where .
-
SPM.1.AHL.TZ0.15b:
Let .
Find the value of for which successive powers of lie on a circle.
-
16N.2.AHL.TZ0.H_12e:
As soon as Mary was 18 she decided to invest of this money in an account of the same type earning 0.4% interest per month. She withdraws every year on her birthday to buy herself a present. Determine how long it will take until there is no money in the account.
-
18M.1.SL.TZ1.T_7b:
On that day, Sergei made 12 successive lifts. Find the total combined weight of these lifts.
-
19M.1.AHL.TZ0.F_3b.ii:
Determine the corresponding eigenvectors.
-
EXM.1.AHL.TZ0.45a:
Given matrices A, B, C for which AB = C and det A ≠ 0, express B in terms of A and C.
-
EXM.1.AHL.TZ0.45c:
Find the coordinates of the point of intersection of the planes , , .
-
16N.2.AHL.TZ0.H_12d:
Mary’s grandparents wished for the amount in her account to be at least the day before she was 18. Determine the minimum value of the monthly deposit required to achieve this. Give your answer correct to the nearest dollar.
-
18N.2.SL.TZ0.T_1c.ii:
Justify whether it is valid to use the regression line y on x to estimate Jerome’s examination score.
-
20N.2.SL.TZ0.T_5c:
Write down the common difference, .
-
20N.2.SL.TZ0.T_5f:
Find the total amount of fuel pumped into the tank in the first hours.
-
20N.2.SL.TZ0.T_5g:
Show that the tank will never be completely filled using this pump.
-
19M.2.SL.TZ2.T_4d.ii:
The daily amount of antibiotic Ted receives will first be less than 0.06 mg on the th day. Find the value of .
-
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
-
SPM.2.AHL.TZ0.3b.ii:
Find the annual interest rate, .
-
EXM.2.AHL.TZ0.8c:
Write down the other two linear equations in , and .
-
19N.2.SL.TZ0.T_3e:
Each triangular pane has an area of .
Find the total area of the decorative glass face, if the maximum number of complete levels were built. Express your area to the nearest .
-
EXM.1.AHL.TZ0.30b:
Hence, or otherwise, find A–1.
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
19M.2.AHL.TZ0.F_3c:
Using mathematical induction, prove that Mn can be written as a quadratic expression in M for all positive integers n ≥ 3.
-
EXM.1.AHL.TZ0.43a:
Find the values of and given that the matrix is the inverse of the matrix .
-
20N.1.AHL.TZ0.F_4b.ii:
Assuming that is non-singular, use the result in part (b)(i) to show that
.
-
20N.2.SL.TZ0.S_6a:
Find the common ratio in terms of .
-
20N.2.SL.TZ0.T_5e.ii:
Write down the number of hours that the pump was pumping fuel into the tank.
-
EXM.2.AHL.TZ0.23b.i:
Find the value of and of .
-
EXM.1.AHL.TZ0.4b.ii:
Given that B , and C , find X.
-
EXM.2.AHL.TZ0.10a.i:
Find A−1.
-
EXM.1.AHL.TZ0.47:
Given that A = and I = , find the values of for which (A – I) is a singular matrix.
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
16N.2.SL.TZ0.T_6e:
Find .
-
EXM.1.AHL.TZ0.22b:
The matrix C = and 2AB = C. Find the value of .
-
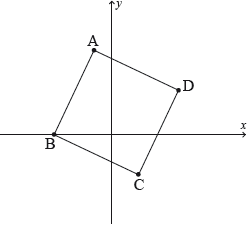
17M.1.AHL.TZ2.H_5:
In the following Argand diagram the point A represents the complex number and the point B represents the complex number . The shape of ABCD is a square. Determine the complex numbers represented by the points C and D.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
Find the angle of elevation of A from D.
-
19N.1.SL.TZ0.T_8b:
After the four-year period, Siân withdraws AUD from her savings account and uses this money to buy a car. It is known that the car will depreciate at a rate of % per year.
The value of the car will be AUD after years.
Find the value of .
-
EXM.3.AHL.TZ0.5d.ii:
Show that .
-
EXN.1.SL.TZ0.9b:
Find an approximation for the real interest rate for the money invested in the account.
-
EXN.1.SL.TZ0.12a:
Write down the value of .
-
EXN.1.SL.TZ0.12b:
Find the value of .
-
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree. -
17M.1.AHL.TZ1.H_1:
Find the solution of .
-
SPM.2.SL.TZ0.1c:
State which option Bryan should choose. Justify your answer.
-
SPM.2.AHL.TZ0.3c:
State which option Bryan should choose. Justify your answer.
-
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
-
EXM.1.AHL.TZ0.43b:
For the values of and found in part (a), solve the system of linear equations
-
EXM.1.AHL.TZ0.6c:
Find D–1.
-
17N.2.AHL.TZ0.H_12a:
Find the amount Phil would owe the bank after 20 years. Give your answer to the nearest dollar.
-
21M.2.SL.TZ1.3d.ii:
the annual interest rate of the loan.
-
EXM.2.AHL.TZ0.7a.ii:
Find 100.
-
EXM.1.AHL.TZ0.35a:
Write down the inverse of the matrix
A =
-
EXM.1.AHL.TZ0.10b:
det (2A − B).
-
EXM.1.AHL.TZ0.6b:
Find CD.
-
19M.2.SL.TZ2.T_4d.i:
Find the amount of antibiotic, in mg, that Ted receives on the fifth day.
-
EXM.2.SL.TZ0.1c.ii:
option 2.
-
EXM.1.SL.TZ0.6b:
Yejin has just turned 28 years old. She currently has no retirement savings. She wants to save part of her salary each month into her annuity fund.
Calculate the amount Yejin needs to save each month, to meet her retirement goal.
-
19N.1.SL.TZ0.T_7c:
The sum of the first terms is greater than .
Find the smallest possible value of .
-
EXM.2.SL.TZ0.1a.i:
the number of months it will take for Paul to repay the loan.
-
18M.2.SL.TZ2.T_4a:
Find the café’s profit during the 11th week.
-
20N.2.SL.TZ0.S_6c:
Find the value of when .
-
19M.2.SL.TZ2.S_10b:
Find the exact value of .
-
17N.2.AHL.TZ0.H_12b:
Show that the total value of Phil’s savings after 20 years is .
-
EXM.1.AHL.TZ0.49:
The square matrix X is such that X3 = 0. Show that the inverse of the matrix (I – X) is I + X + X2.
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.2.SL.TZ2.S_4c:
Find the least value of n for which Sn > 163.
-
19M.1.AHL.TZ0.F_3a.ii:
Deduce that the eigenvalues are real if A is symmetric.
-
EXM.1.AHL.TZ0.11c:
Find AB.
-
18M.1.AHL.TZ2.H_11b:
Express in terms of . Give your answer in the form , where p , q are constants.
-
18M.2.AHL.TZ1.H_7a:
Show that there will be approximately 2645 fish in the lake at the start of 2020.
-
16N.1.SL.TZ0.S_9c:
Find , giving your answer as an integer.
-
EXM.2.AHL.TZ0.21b.i:
find and in terms of .
-
18M.2.SL.TZ1.T_3c:
Calculate the amount of this investment, in INR, in this account after five years.
-
EXM.1.AHL.TZ0.10a:
2A − B.
-
19N.2.SL.TZ0.T_3c:
Hence, find the total number of panes in a glass face with levels.
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
16N.2.AHL.TZ0.H_12b:
(i) Write down a similar expression for and .
(ii) Hence show that the amount in Mary’s account the day before she turned 10 years old is given by .
-
17N.1.SL.TZ0.S_10a:
The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are , where .
Show that .
-
EXM.1.AHL.TZ0.4a:
Write down the inverse, A–1.
-
18M.2.SL.TZ1.S_7b:
Hence find the value of n such that .
-
19M.2.SL.TZ2.T_4c:
Calculate the total amount of the drug, in mg, that she receives.
-
20N.1.AHL.TZ0.F_4b.i:
Verify that
0.
-
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
-
20N.2.SL.TZ0.T_5b:
Show that the volume of the tank is , correct to three significant figures.
-
17N.1.SL.TZ0.T_3a:
Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.
-
EXM.1.AHL.TZ0.44:
Find the values of the real number for which the determinant of the matrix is equal to zero.
-
EXM.1.AHL.TZ0.52b:
Hence solve the system of equations
-
EXM.2.AHL.TZ0.22b:
Hence show that M is a singular matrix.
-
EXM.2.AHL.TZ0.8d.ii:
Solve this matrix equation.
-
21M.1.SL.TZ2.10b:
Tommaso wants to invest his money in an account such that his investment will increase to times the initial amount in years. Assume the account pays a nominal annual interest of compounded quarterly.
Determine the value of .
-
19M.2.SL.TZ2.S_10d:
An infinite geometric series is given as , .
Find the largest value of such that .
-
17M.2.SL.TZ1.T_1e:
Find the percentage error in your estimate in part (d).
-
18M.2.AHL.TZ1.H_7b:
Find the approximate number of fish in the lake at the start of 2042.
-
21M.2.AHL.TZ2.7a:
Find the eigenvalues and corresponding eigenvectors of the matrix .
-
EXM.3.AHL.TZ0.5e.ii:
Hence, find the Cartesian equation satisfied by and .
-
17M.1.AHL.TZ1.H_2b:
Find the smallest positive integer value of , such that is a real number.
-
SPM.1.SL.TZ0.8a:
An orchestra has a sound intensity of 6.4 × 10−3 W m−2 . Calculate the intensity level, of the orchestra.
-
EXM.1.AHL.TZ0.22a:
Find AB.
-
18M.1.AHL.TZ1.H_11b:
Show that the area of the quadrilateral Q is .
-
EXM.1.AHL.TZ0.35c:
A fourth plane with equation passes through the point of intersection. Find the value of .
-
EXM.1.AHL.TZ0.52a:
Find the inverse of the matrix .
-
17N.2.SL.TZ0.T_3b:
Calculate angle .
-
17M.1.AHL.TZ1.H_2a.i:
By expressing and in modulus-argument form write down the modulus of ;
-
19M.2.SL.TZ1.S_7a:
Write down the first three non-zero terms of .
-
20N.2.SL.TZ0.T_5a:
Find , the height of the tank.
-
EXM.1.AHL.TZ0.30a:
Given that AB = , find .
-
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
EXM.3.AHL.TZ0.5e.i:
Verify that .
-
SPM.1.SL.TZ0.8b:
A rock concert has an intensity level of 112 dB. Find the sound intensity, .
-
SPM.2.AHL.TZ0.3d:
Bryan chooses option B. The car dealership invests the money Bryan pays as soon as they receive it.
If they invest it in an account paying 0.4 % interest per month and inflation is 0.1 % per month, calculate the real amount of money the car dealership has received by the end of the 6 year period.
-
EXM.1.AHL.TZ0.25a:
Find the matrix A2.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
EXM.2.AHL.TZ0.3b:
If is equal to , find the value of .
-
21M.1.AHL.TZ1.9a.ii:
.
-
21M.1.AHL.TZ1.9a.i:
.
-
17M.2.SL.TZ1.T_1c:
Write down the equation of the regression line on , in the form .
-
21M.3.AHL.TZ1.1h.iii:
Find, in hours, the shortest time from sunrise to sunset at point that is predicted by this model.
-
EXM.1.AHL.TZ0.50:
Given that A = and B = , find X if BX = A – AB.
-
SPM.2.SL.TZ0.1d:
Bryan’s car depreciates at an annual rate of 25 % per year.
Find the value of Bryan’s car six years after it is purchased.
-
EXM.2.AHL.TZ0.22d:
Show that (I − M)2 = I − M where I is the identity matrix.
-
17M.1.SL.TZ2.T_5a:
Diagram is formed with 52 sticks. Find the value of .
-
21M.1.SL.TZ1.8a.i:
Charlie ran on day of his fitness programme.
-
20N.2.SL.TZ0.S_6b:
Find the values of for which the sum to infinity of the series exists.
-
20N.2.SL.TZ0.T_5d:
Find the amount of fuel pumped into the tank in the hour.
-
19N.2.SL.TZ0.T_3a:
Find the number of triangular panes in the level.
-
21M.2.SL.TZ1.3c:
Write down the amount of the loan.
-
21M.2.SL.TZ1.3e:
Find the amount of Daisy’s final payment.
-
21M.2.SL.TZ1.3d.i:
the amount of interest paid by Daisy.
-
21M.2.SL.TZ1.3f:
Find how much money Daisy saved by making one final payment after years.
-
21M.2.AHL.TZ1.5d:
Hence find the long-term percentage of sunny days in Vokram.
-
SPM.1.SL.TZ0.2c:
Find the total cost of buying 2 tickets in each of the first 16 rows.
-
21M.2.SL.TZ1.3a:
Calculate the value of Daisy’s investment after years.
-
EXM.2.AHL.TZ0.23b.ii:
Hence show that I = A (6I – A).
-
EXM.1.AHL.TZ0.33:
Given that M = and that M2 – 6M + kI = 0 find k.
-
18M.1.AHL.TZ1.H_11c:
Let . The points represented on an Argand diagram by form the vertices of a polygon .
Show that the area of the polygon can be expressed in the form , where .
-
17M.1.SL.TZ1.T_5a:
Find the distance from the base of this ladder to the top rung.
-
EXM.2.AHL.TZ0.22a.i:
Show that .
-
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
19N.1.SL.TZ0.T_7b:
Write down the second term of this sequence.
-
EXM.3.AHL.TZ0.5c.ii:
Hence, show that .
-
EXM.2.AHL.TZ0.22a.ii:
Find an expression for in terms of .
-
EXM.1.AHL.TZ0.48:
The matrices A, B, C and X are all non-singular 3 × 3 matrices.
Given that A–1XB = C, express X in terms of the other matrices.
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
19N.2.SL.TZ0.T_3d:
Find the maximum number of complete levels that Maegan can build.
-
18M.1.SL.TZ2.S_7b:
Let and . Find the value of .
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
21M.1.SL.TZ2.10a:
Calculate the amount Pietro will have in his account after years. Give your answer correct to decimal places.
-
EXM.1.AHL.TZ0.11b:
Find −3A.
-
EXM.2.AHL.TZ0.10a.ii:
Find A2.
-
21M.3.AHL.TZ1.1h.ii:
Hence or otherwise find an equation for in the form , where .
-
EXM.2.AHL.TZ0.10d:
Let X be a 2 × 2 matrix such that AX = B. Find X.
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
20N.1.AHL.TZ0.F_4a:
By considering the determinant of a relevant matrix, show that the eigenvalues, , of satisfy the equation
,
where and are functions of to be determined.
-
21M.1.AHL.TZ2.5a:
Estimate the value of Roger’s laptop after years.
-
21M.1.AHL.TZ2.5c:
Comment on the validity of your answer to part (b).
-
21M.1.AHL.TZ2.7a:
Find how high the balloon will travel in the first minutes after it is launched.
-
21M.1.AHL.TZ2.7c:
Suggest a limitation of the given model.
-
18M.1.AHL.TZ0.F_2b:
Let B = .
Given that B2 – B – 4I = , find the value of .
-
21M.2.SL.TZ2.3a.ii:
the total number of seats in the concert hall.
-
21M.2.SL.TZ2.3a.i:
the number of seats in the last row.
-
21M.2.SL.TZ2.3b:
Find the average number of visitors per concert in .
-
21M.2.SL.TZ2.3d:
It is assumed that the concert hall will host concerts each year.
Use the average number of visitors per concert per year to predict the total number of people expected to attend the concert hall from when it opens until the end of .
-
EXM.1.AHL.TZ0.2:
If and det , find the possible values of .
-
17M.1.AHL.TZ2.H_3a:
the value of ;
-
19M.2.SL.TZ2.T_4a.ii:
Write down an equation, in terms of and , for the amount of the drug that she receives on the eleventh day.
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
18M.1.AHL.TZ2.H_5b:
A particular geometric sequence has u1 = 3 and a sum to infinity of 4.
Find the value of d.
-
19M.2.SL.TZ1.S_7b.ii:
Find the value of .
-
21M.2.AHL.TZ2.4a:
Write down a transition matrix indicating the annual population movement between clinics.
-
17N.2.SL.TZ0.T_3a:
Show that correct to the nearest metre.
-
18M.2.SL.TZ1.T_3a:
Calculate the value of r.
-
17N.2.AHL.TZ0.H_12d.i:
David wishes to withdraw $5000 at the end of each year for a period of years. Show that an expression for the minimum value of is
.
-
21M.2.AHL.TZ2.7e:
Sketch a phase portrait for the general solution to the system of coupled differential equations for , .
-
21M.2.AHL.TZ2.7b:
Hence, write down the general solution of the system.
-
19M.2.SL.TZ2.S_10c:
Show that .
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
EXM.1.AHL.TZ0.29c:
Show that det(M2) is positive.
-
20N.2.SL.TZ0.T_5e.i:
Find the value of such that .
-
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.
Find the least value of such that the th term of the sequence is less than 7.
-
EXM.1.AHL.TZ0.32:
If A = and A2 is a matrix whose entries are all 0, find .
-
EXM.1.SL.TZ0.1b:
The rate of inflation during this 10 year period is 1.5% per year.
Calculate the real value of her savings after 10 years.
-
21M.2.AHL.TZ2.7c:
Determine, with justification, whether the equilibrium point is stable or unstable.
-
EXM.1.AHL.TZ0.26c:
Find A(A–1B + 2A–1)A.
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
16N.2.AHL.TZ0.H_12c:
Write down an expression for in terms of on the day before Mary turned 18 years old showing clearly the value of .
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
EXM.1.AHL.TZ0.26a:
Find BA.
-
EXN.1.SL.TZ0.9a:
Find the value of her investment after a period of years.
-
EXN.1.AHL.TZ0.14a:
Write down in exponential form.
-
EXN.3.AHL.TZ0.2a:
Find an expression for the width of in centimetres.
-
EXN.3.AHL.TZ0.2d.ii:
hence find .
-
EXN.1.SL.TZ0.5a:
Find the value for a solution in which the hydrogen ion concentration is .
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
EXN.1.SL.TZ0.9c:
Hence find the real value of Sophia’s investment at the end of years.
-
EXN.1.SL.TZ0.12c:
A game is played in which the arrow attached to the centre of the disc is spun and the sector in which the arrow stops is noted. If the arrow stops in sector the player wins points, otherwise they lose points.
Let be the number of points won
Find .
-
19M.2.SL.TZ2.S_10a:
Find the value of .
-
20N.1.SL.TZ0.T_8b:
At the end of the years, Imon withdrew from the fixed deposit account and reinvested this into a super-savings account with a nominal annual interest rate of , compounded half-yearly.
The value of the super-savings account increased to after months.
Find the value of .
-
19M.2.SL.TZ1.S_7b.i:
Find the value of .
-
21M.2.AHL.TZ2.4b:
Find a prediction for the ratio of the number of patients Doctor Black will have, compared to Doctor Green, after two years.
-
EXN.1.SL.TZ0.5b.ii:
Find the hydrogen ion concentration in a solution with . Give your answer in the form where and is an integer.
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.
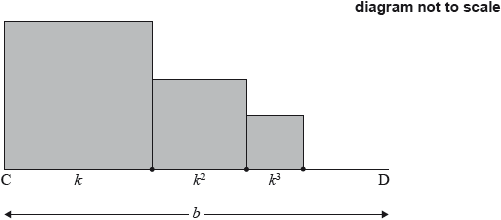
The total sum of the areas of all the squares is . Find the value of .
-
21M.3.AHL.TZ1.1h.i:
Write down and in exponential form, with a constant modulus.
-
16N.1.SL.TZ0.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
EXM.1.AHL.TZ0.25b:
If det A2 = 16, determine the possible values of .
-
19M.2.AHL.TZ1.H_11c:
Given that , find the other two real roots.
-
21M.1.SL.TZ1.8a.ii:
Daniella ran on day of her fitness programme.
-
21M.1.SL.TZ1.9:
A triangular field is such that and , each measured correct to the nearest metre, and the angle at is equal to , measured correct to the nearest .
Calculate the maximum possible area of the field.
-
21M.1.AHL.TZ2.5b:
Find the value of .
-
21M.1.AHL.TZ2.7b:
The balloon is required to reach a height of at least metres.
Determine whether it will reach this height. -
21M.1.AHL.TZ2.12b:
Find the least value of such that .
-
21M.1.SL.TZ1.1a:
Calculate Katya’s approximation of , correct to four decimal places.
-
21M.1.SL.TZ1.1b:
Calculate the percentage error in using Katya’s four decimal place approximation of , compared to the exact value of in your calculator.
-
21M.1.AHL.TZ1.9c:
Hence, or otherwise, find the value of when .
-
21M.2.AHL.TZ1.5c.i:
Write down the matrix .
-
21M.1.AHL.TZ2.12a.ii:
Find the value of for .
-
21M.2.AHL.TZ2.4c:
Find a matrix , with integer elements, such that , where is a diagonal matrix.
-
21M.2.AHL.TZ2.4d:
Hence, show that the long-term transition matrix is given by .
-
21M.2.AHL.TZ2.4e:
Hence, or otherwise, determine the expected ratio of the number of patients Doctor Black would have compared to Doctor Green in the long term.
-
21M.2.AHL.TZ2.7d:
(i) at .
(ii) at .
-
21N.1.AHL.TZ0.6a:
Find the common ratio, , for the sequence.
-
21N.2.AHL.TZ0.5a.i:
Plot the position of on an Argand Diagram.
-
EXN.3.AHL.TZ0.2h:
After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.
Describe the animation for these two revolutions, stating the final position of the sequence of squares.
-
21N.2.AHL.TZ0.5a.ii:
Express in the form , where , giving the exact value of and the exact value of .
-
EXN.2.AHL.TZ0.5e.ii:
Find the population of at this value of . Give your answer to the nearest herbivores.
-
EXN.2.AHL.TZ0.5a.ii:
the eigenvectors.
-
EXN.2.AHL.TZ0.5b:
Hence write down the general solution of the system of equations.
-
EXN.2.AHL.TZ0.5c:
Sketch the phase portrait for this system, for .
On your sketch show
- the equation of the line defined by the eigenvector in the first quadrant
- at least two trajectories either side of this line using arrows on those trajectories to represent the change in populations as t increases
-
EXN.3.AHL.TZ0.2f.iii:
Hence find the image of after it is rotated and enlarged.
-
EXN.3.AHL.TZ0.2b:
Given the width of a pixel is approximately , find the number of squares in the final image.
-
EXN.3.AHL.TZ0.2d.iii:
show that .
-
EXN.3.AHL.TZ0.2e:
Hence or otherwise, find the coordinates of the top left-hand corner in .
-
EXN.3.AHL.TZ0.2f.i:
Find, , in the form .
-
21N.2.AHL.TZ0.5c.ii:
Find the phase shift of .
-
21N.1.SL.TZ0.6a:
Use the trapezoidal rule with an interval width of to estimate the total amount of carbon dioxide emitted during these two hours.
-
21N.1.SL.TZ0.6b:
The real amount of carbon dioxide emitted during these two hours was tonnes.
Find the percentage error of the estimate found in part (a).
-
21N.1.SL.TZ0.10a:
Find the amount they will pay the bank each month.
-
21N.1.SL.TZ0.10b.ii:
Using your answers to parts (a) and (b)(i), calculate how much interest they will have paid in total during the first years.
-
21N.2.SL.TZ0.2a:
Calculate the percentage increase in applications from the first year to the second year.
-
21N.2.SL.TZ0.2b.ii:
Find an expression for .
-
21N.2.SL.TZ0.2b.iii:
Find the number of student applications the university expects to receive when . Express your answer to the nearest integer.
-
21N.2.SL.TZ0.2c:
Write down an expression for .
-
21N.2.SL.TZ0.2d:
Calculate the total amount of acceptance fees paid to the university in the first years.
-
21N.2.SL.TZ0.2e:
Find .
-
21N.2.AHL.TZ0.6b:
Write down the matrix .
-
21N.2.AHL.TZ0.6d:
Given that when the shock absorber is displaced and its velocity is zero, find an expression for in terms of .
Sub sections and their related questions
SL 1.1—Using standard form
-
16N.1.SL.TZ0.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
17N.1.SL.TZ0.T_3a:
Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.
-
20N.1.SL.TZ0.T_1a:
Write down the value of the iron in the form where .
-
20N.1.SL.TZ0.T_1b:
Calculate James’s estimate of its volume, in .
-
20N.1.SL.TZ0.T_1c:
The actual volume of the asteroid is found to be .
Find the percentage error in James’s estimate of the volume.
-
EXN.1.SL.TZ0.5a:
Find the value for a solution in which the hydrogen ion concentration is .
-
EXN.1.SL.TZ0.5b.i:
Write an expression for in terms of .
-
EXN.1.SL.TZ0.5b.ii:
Find the hydrogen ion concentration in a solution with . Give your answer in the form where and is an integer.
-
22M.1.SL.TZ2.4a:
Calculate the pH of the coffee.
-
22M.2.SL.TZ1.2d:
Find the total area of the tiles in Eddie’s path. Give your answer in the form where and is an integer.
- 957233: This is an example question for the example test. You can delete this question.
SL 1.2—Arithmetic sequences and series
-
SPM.1.SL.TZ0.2a:
Write down the value of the common difference,
-
SPM.1.SL.TZ0.2b:
Calculate the price of a ticket in the 16th row.
-
SPM.1.SL.TZ0.2c:
Find the total cost of buying 2 tickets in each of the first 16 rows.
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
17M.1.AHL.TZ1.H_7a:
find the value of .
-
17M.1.AHL.TZ1.H_7b:
determine the value of .
-
17M.1.AHL.TZ2.H_3a:
the value of ;
-
17M.1.AHL.TZ2.H_3b:
the value of ;
-
18M.2.AHL.TZ1.H_1a:
Find the first term and the common difference of the sequence.
-
18M.2.AHL.TZ1.H_1b:
Calculate the number of positive terms in the sequence.
-
18M.2.AHL.TZ1.H_7a:
Show that there will be approximately 2645 fish in the lake at the start of 2020.
-
18M.2.AHL.TZ1.H_7b:
Find the approximate number of fish in the lake at the start of 2042.
-
18M.1.AHL.TZ2.H_5a:
Show that A is an arithmetic sequence, stating its common difference d in terms of r.
-
18M.1.AHL.TZ2.H_5b:
A particular geometric sequence has u1 = 3 and a sum to infinity of 4.
Find the value of d.
-
19M.2.AHL.TZ2.H_7:
Suppose that is the first term of a geometric series with common ratio .
Prove, by mathematical induction, that the sum of the first terms, is given by
, where .
-
16N.1.AHL.TZ0.H_6a:
Write down the value of .
-
16N.1.AHL.TZ0.H_6b:
Find the value of .
-
16N.1.AHL.TZ0.H_6c:
Prove that is an arithmetic sequence, stating clearly its common difference.
-
16N.2.AHL.TZ0.H_12a:
Find an expression for and show that .
-
16N.2.AHL.TZ0.H_12b:
(i) Write down a similar expression for and .
(ii) Hence show that the amount in Mary’s account the day before she turned 10 years old is given by .
-
16N.2.AHL.TZ0.H_12c:
Write down an expression for in terms of on the day before Mary turned 18 years old showing clearly the value of .
-
16N.2.AHL.TZ0.H_12d:
Mary’s grandparents wished for the amount in her account to be at least the day before she was 18. Determine the minimum value of the monthly deposit required to achieve this. Give your answer correct to the nearest dollar.
-
16N.2.AHL.TZ0.H_12e:
As soon as Mary was 18 she decided to invest of this money in an account of the same type earning 0.4% interest per month. She withdraws every year on her birthday to buy herself a present. Determine how long it will take until there is no money in the account.
-
19M.1.AHL.TZ2.H_1:
In an arithmetic sequence, the sum of the 3rd and 8th terms is 1.
Given that the sum of the first seven terms is 35, determine the first term and the common difference.
-
17N.1.SL.TZ0.S_2a:
Find the common difference.
-
17N.1.SL.TZ0.S_2b:
Find the tenth term.
-
17N.1.SL.TZ0.S_2c:
Find the sum of the first ten terms.
-
18M.2.SL.TZ1.S_7a:
Given that xk + 1 = xk + a, find a.
-
18M.2.SL.TZ1.S_7b:
Hence find the value of n such that .
-
18M.1.SL.TZ2.S_7b:
Let and . Find the value of .
-
19M.2.SL.TZ2.S_10a:
Find the value of .
-
19M.2.SL.TZ2.S_10b:
Find the exact value of .
-
19M.2.SL.TZ2.S_10c:
Show that .
-
19M.2.SL.TZ2.S_10d:
An infinite geometric series is given as , .
Find the largest value of such that .
-
18N.1.SL.TZ0.S_3a:
Find u8.
-
18N.2.SL.TZ0.S_5:
The sum of an infinite geometric sequence is 33.25. The second term of the sequence is 7.98. Find the possible values of .
-
16N.1.SL.TZ0.S_9a:
Find .
-
16N.1.SL.TZ0.S_9b:
Show that the sum of the infinite sequence is .
-
16N.1.SL.TZ0.S_9c:
Find , giving your answer as an integer.
-
16N.1.SL.TZ0.S_9d:
Show that .
-
16N.1.SL.TZ0.S_9e:
Given that is equal to half the sum of the infinite geometric sequence, find , giving your answer in the form , where .
-
19M.2.SL.TZ1.S_7a:
Write down the first three non-zero terms of .
-
19M.2.SL.TZ1.S_7b.i:
Find the value of .
-
19M.2.SL.TZ1.S_7b.ii:
Find the value of .
-
19M.2.SL.TZ2.T_4a.i:
Write down an equation, in terms of and , for the amount of the drug that she receives on the seventh day.
-
19M.2.SL.TZ2.T_4a.ii:
Write down an equation, in terms of and , for the amount of the drug that she receives on the eleventh day.
-
19M.2.SL.TZ2.T_4b:
Write down the value of and the value of .
-
19M.2.SL.TZ2.T_4c:
Calculate the total amount of the drug, in mg, that she receives.
-
19M.2.SL.TZ2.T_4d.i:
Find the amount of antibiotic, in mg, that Ted receives on the fifth day.
-
19M.2.SL.TZ2.T_4d.ii:
The daily amount of antibiotic Ted receives will first be less than 0.06 mg on the th day. Find the value of .
-
19M.2.SL.TZ2.T_4d.iii:
Hence find the total amount of antibiotic, in mg, that Ted receives during the first days.
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.1.SL.TZ1.T_7a.i:
For that day find how much weight was added after each lift.
-
18M.1.SL.TZ1.T_7a.ii:
For that day find the weight of Sergei’s first lift.
-
18M.1.SL.TZ1.T_7b:
On that day, Sergei made 12 successive lifts. Find the total combined weight of these lifts.
-
18M.2.SL.TZ2.T_4a:
Find the café’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4c:
Find the tea-shop’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4e:
In the mth week the tea-shop’s total profit exceeds the café’s total profit, for the first time since they both opened.
Find the value of m.
-
17M.1.SL.TZ2.T_5a:
Diagram is formed with 52 sticks. Find the value of .
-
17M.1.SL.TZ2.T_5b:
Find the total number of sticks used by Tomás for all 24 diagrams.
-
17M.1.SL.TZ1.T_5a:
Find the distance from the base of this ladder to the top rung.
-
17M.1.SL.TZ1.T_5b:
The company also makes a ladder that is 1050 cm long.
Find the maximum number of rungs in this 1050 cm long ladder.
-
19N.2.SL.TZ0.T_3a:
Find the number of triangular panes in the level.
-
19N.2.SL.TZ0.T_3b:
Show that the total number of triangular panes, , in the first levels is given by:
.
-
19N.2.SL.TZ0.T_3c:
Hence, find the total number of panes in a glass face with levels.
-
19N.2.SL.TZ0.T_3d:
Find the maximum number of complete levels that Maegan can build.
-
19N.2.SL.TZ0.T_3e:
Each triangular pane has an area of .
Find the total area of the decorative glass face, if the maximum number of complete levels were built. Express your area to the nearest .
-
20N.2.SL.TZ0.T_5a:
Find , the height of the tank.
-
20N.2.SL.TZ0.T_5b:
Show that the volume of the tank is , correct to three significant figures.
-
20N.2.SL.TZ0.T_5c:
Write down the common difference, .
-
20N.2.SL.TZ0.T_5d:
Find the amount of fuel pumped into the tank in the hour.
-
20N.2.SL.TZ0.T_5e.i:
Find the value of such that .
-
20N.2.SL.TZ0.T_5e.ii:
Write down the number of hours that the pump was pumping fuel into the tank.
-
20N.2.SL.TZ0.T_5f:
Find the total amount of fuel pumped into the tank in the first hours.
-
20N.2.SL.TZ0.T_5g:
Show that the tank will never be completely filled using this pump.
-
EXN.1.SL.TZ0.12a:
Write down the value of .
-
EXN.1.SL.TZ0.12b:
Find the value of .
-
EXN.1.SL.TZ0.12c:
A game is played in which the arrow attached to the centre of the disc is spun and the sector in which the arrow stops is noted. If the arrow stops in sector the player wins points, otherwise they lose points.
Let be the number of points won
Find .
-
EXN.3.AHL.TZ0.2a:
Find an expression for the width of in centimetres.
-
EXN.3.AHL.TZ0.2b:
Given the width of a pixel is approximately , find the number of squares in the final image.
-
21M.1.SL.TZ1.8a.i:
Charlie ran on day of his fitness programme.
-
21M.1.SL.TZ1.8a.ii:
Daniella ran on day of her fitness programme.
-
21M.2.SL.TZ2.3a.i:
the number of seats in the last row.
-
21M.2.SL.TZ2.3a.ii:
the total number of seats in the concert hall.
-
21N.2.SL.TZ0.2a:
Calculate the percentage increase in applications from the first year to the second year.
-
21N.2.SL.TZ0.2b.i:
Write down the common ratio of the sequence.
-
21N.2.SL.TZ0.2b.ii:
Find an expression for .
-
21N.2.SL.TZ0.2b.iii:
Find the number of student applications the university expects to receive when . Express your answer to the nearest integer.
-
21N.2.SL.TZ0.2c:
Write down an expression for .
-
21N.2.SL.TZ0.2d:
Calculate the total amount of acceptance fees paid to the university in the first years.
-
21N.2.SL.TZ0.2e:
Find .
-
21N.2.SL.TZ0.2f:
State whether, for all , the university will have places available for all applicants. Justify your answer.
-
22M.2.SL.TZ1.2a.i:
.
-
22M.2.SL.TZ1.2a.ii:
.
-
22M.2.SL.TZ1.2b.i:
.
-
22M.2.SL.TZ1.2b.ii:
.
-
22M.2.SL.TZ1.2c.i:
Show that Eddie needs tiles.
-
22M.2.SL.TZ1.2c.ii:
Find the value of for this path.
-
22M.2.SL.TZ2.2a.i:
fed to the dog per day.
-
22M.2.SL.TZ2.2a.ii:
remaining in the bag at the end of the first day.
-
22M.2.SL.TZ2.2b:
Calculate the number of days that Scott can feed his dog with one bag of food.
-
22M.2.SL.TZ2.2c:
Determine the amount that Scott expects to spend on dog food in . Round your answer to the nearest dollar.
SL 1.3—Geometric sequences and series
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
-
19M.2.AHL.TZ1.H_11c:
Given that , find the other two real roots.
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
18M.2.SL.TZ2.S_4a:
Find the common ratio.
-
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
-
18M.2.SL.TZ2.S_4c:
Find the least value of n for which Sn > 163.
-
17N.1.SL.TZ0.S_10a:
The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are , where .
Show that .
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.

The total sum of the areas of all the squares is . Find the value of .
-
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.
Find the least value of such that the th term of the sequence is less than 7.
-
19M.2.SL.TZ2.T_4a.i:
Write down an equation, in terms of and , for the amount of the drug that she receives on the seventh day.
-
19M.2.SL.TZ2.T_4a.ii:
Write down an equation, in terms of and , for the amount of the drug that she receives on the eleventh day.
-
19M.2.SL.TZ2.T_4b:
Write down the value of and the value of .
-
19M.2.SL.TZ2.T_4c:
Calculate the total amount of the drug, in mg, that she receives.
-
19M.2.SL.TZ2.T_4d.i:
Find the amount of antibiotic, in mg, that Ted receives on the fifth day.
-
19M.2.SL.TZ2.T_4d.ii:
The daily amount of antibiotic Ted receives will first be less than 0.06 mg on the th day. Find the value of .
-
19M.2.SL.TZ2.T_4d.iii:
Hence find the total amount of antibiotic, in mg, that Ted receives during the first days.
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.2.SL.TZ2.T_4a:
Find the café’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4c:
Find the tea-shop’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
18M.2.SL.TZ2.T_4e:
In the mth week the tea-shop’s total profit exceeds the café’s total profit, for the first time since they both opened.
Find the value of m.
-
17M.1.SL.TZ2.T_9a:
Write down the common ratio of the sequence.
-
19N.1.SL.TZ0.T_7a:
Find the common ratio.
-
19N.1.SL.TZ0.T_7b:
Write down the second term of this sequence.
-
19N.1.SL.TZ0.T_7c:
The sum of the first terms is greater than .
Find the smallest possible value of .
-
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
-
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
-
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of .
Find the total number of slices Mia can cut from this pie.
-
EXN.3.AHL.TZ0.2d.i:
state the coordinates, , of its image in .
-
EXN.3.AHL.TZ0.2d.ii:
hence find .
-
EXN.3.AHL.TZ0.2d.iii:
show that .
-
EXN.3.AHL.TZ0.2e:
Hence or otherwise, find the coordinates of the top left-hand corner in .
-
EXN.3.AHL.TZ0.2f.i:
Find, , in the form .
-
EXN.3.AHL.TZ0.2f.ii:
Write down .
-
EXN.3.AHL.TZ0.2f.iii:
Hence find the image of after it is rotated and enlarged.
-
EXN.3.AHL.TZ0.2g:
Find the value of at which the enlargement scale factor equals zero.
-
EXN.3.AHL.TZ0.2h:
After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.
Describe the animation for these two revolutions, stating the final position of the sequence of squares.
-
21M.1.SL.TZ1.8a.i:
Charlie ran on day of his fitness programme.
-
21M.1.SL.TZ1.8a.ii:
Daniella ran on day of her fitness programme.
-
21M.1.AHL.TZ2.7a:
Find how high the balloon will travel in the first minutes after it is launched.
-
21M.1.AHL.TZ2.7b:
The balloon is required to reach a height of at least metres.
Determine whether it will reach this height. -
21M.1.AHL.TZ2.7c:
Suggest a limitation of the given model.
-
21M.2.SL.TZ2.3b:
Find the average number of visitors per concert in .
-
21M.2.SL.TZ2.3d:
It is assumed that the concert hall will host concerts each year.
Use the average number of visitors per concert per year to predict the total number of people expected to attend the concert hall from when it opens until the end of .
-
21N.1.AHL.TZ0.6a:
Find the common ratio, , for the sequence.
-
21N.1.AHL.TZ0.6b:
Find the least value of such that .
-
21N.2.SL.TZ0.2a:
Calculate the percentage increase in applications from the first year to the second year.
-
21N.2.SL.TZ0.2b.i:
Write down the common ratio of the sequence.
-
21N.2.SL.TZ0.2b.ii:
Find an expression for .
-
21N.2.SL.TZ0.2b.iii:
Find the number of student applications the university expects to receive when . Express your answer to the nearest integer.
-
21N.2.SL.TZ0.2c:
Write down an expression for .
-
21N.2.SL.TZ0.2d:
Calculate the total amount of acceptance fees paid to the university in the first years.
-
21N.2.SL.TZ0.2e:
Find .
-
21N.2.SL.TZ0.2f:
State whether, for all , the university will have places available for all applicants. Justify your answer.
-
22M.1.SL.TZ1.13a:
Show that the maximum height reached by the ball after it has bounced for the sixth time is , to the nearest .
-
22M.1.SL.TZ1.13b:
Find the number of times, after the first bounce, that the maximum height reached is greater than .
-
22M.1.SL.TZ1.13c:
Find the total vertical distance travelled by the ball from the point at which it is dropped until the fourth bounce.
-
22M.1.AHL.TZ2.7:
The sum of an infinite geometric sequence is .
The first term is more than the second term.
Find the third term. Justify your answer.
-
22M.2.SL.TZ2.2d.i:
Calculate the value of .
-
22M.2.SL.TZ2.2d.ii:
Describe what the value in part (d)(i) represents in this context.
SL 1.4—Financial apps – compound interest, annual depreciation
-
SPM.2.SL.TZ0.1a.i:
Find the repayment made each quarter.
-
SPM.2.SL.TZ0.1a.ii:
Find the total amount paid for the car.
-
SPM.2.SL.TZ0.1a.iii:
Find the interest paid on the loan.
-
SPM.2.SL.TZ0.1b.i:
Find the amount to be borrowed for this option.
-
SPM.2.SL.TZ0.1b.ii:
Find the annual interest rate, .
-
SPM.2.SL.TZ0.1c:
State which option Bryan should choose. Justify your answer.
-
SPM.2.SL.TZ0.1d:
Bryan’s car depreciates at an annual rate of 25 % per year.
Find the value of Bryan’s car six years after it is purchased.
-
SPM.2.AHL.TZ0.3a.i:
Find the repayment made each quarter.
-
SPM.2.AHL.TZ0.3a.ii:
Find the total amount paid for the car.
-
SPM.2.AHL.TZ0.3a.iii:
Find the interest paid on the loan.
-
SPM.2.AHL.TZ0.3b.i:
Find the amount to be borrowed for this option.
-
SPM.2.AHL.TZ0.3b.ii:
Find the annual interest rate, .
-
SPM.2.AHL.TZ0.3c:
State which option Bryan should choose. Justify your answer.
-
SPM.2.AHL.TZ0.3d:
Bryan chooses option B. The car dealership invests the money Bryan pays as soon as they receive it.
If they invest it in an account paying 0.4 % interest per month and inflation is 0.1 % per month, calculate the real amount of money the car dealership has received by the end of the 6 year period.
-
EXM.1.SL.TZ0.1a:
Calculate the value of her savings after 10 years.
-
EXM.1.SL.TZ0.1b:
The rate of inflation during this 10 year period is 1.5% per year.
Calculate the real value of her savings after 10 years.
-
18M.1.SL.TZ2.T_4a:
Complete the second column of the table by giving one example of a number from each set.
-
18M.1.SL.TZ2.T_4b:
Josh states: “Every integer is a natural number”.
Write down whether Josh’s statement is correct. Justify your answer.
-
18M.2.SL.TZ1.T_3a:
Calculate the value of r.
-
18M.2.SL.TZ1.T_3b:
Calculate 14 000 USD in INR.
-
18M.2.SL.TZ1.T_3c:
Calculate the amount of this investment, in INR, in this account after five years.
-
18M.2.SL.TZ1.T_3d:
Harinder chose option B. At the end of five years, Harinder converted this investment back to USD. The exchange rate, at that time, was 1 USD = 67.16 INR.
Calculate how much more money, in USD, Harinder earned by choosing option B instead of option A.
-
17N.2.AHL.TZ0.H_12a:
Find the amount Phil would owe the bank after 20 years. Give your answer to the nearest dollar.
-
17N.2.AHL.TZ0.H_12b:
Show that the total value of Phil’s savings after 20 years is .
-
17N.2.AHL.TZ0.H_12c:
Given that Phil’s aim is to own the house after 20 years, find the value for to the nearest dollar.
-
17N.2.AHL.TZ0.H_12d.i:
David wishes to withdraw $5000 at the end of each year for a period of years. Show that an expression for the minimum value of is
.
-
17N.2.AHL.TZ0.H_12d.ii:
Hence or otherwise, find the minimum value of that would permit David to withdraw annual amounts of $5000 indefinitely. Give your answer to the nearest dollar.
-
19N.1.SL.TZ0.T_8a:
Calculate the value of Siân’s investment after four years. Give your answer correct to two decimal places.
-
19N.1.SL.TZ0.T_8b:
After the four-year period, Siân withdraws AUD from her savings account and uses this money to buy a car. It is known that the car will depreciate at a rate of % per year.
The value of the car will be AUD after years.
Find the value of .
-
20N.1.SL.TZ0.T_8a:
Calculate the value of Imon’s investment after years.
-
20N.1.SL.TZ0.T_8b:
At the end of the years, Imon withdrew from the fixed deposit account and reinvested this into a super-savings account with a nominal annual interest rate of , compounded half-yearly.
The value of the super-savings account increased to after months.
Find the value of .
-
EXN.1.SL.TZ0.9a:
Find the value of her investment after a period of years.
-
EXN.1.SL.TZ0.9b:
Find an approximation for the real interest rate for the money invested in the account.
-
EXN.1.SL.TZ0.9c:
Hence find the real value of Sophia’s investment at the end of years.
-
21M.2.SL.TZ1.3a:
Calculate the value of Daisy’s investment after years.
-
21M.2.SL.TZ1.3b:
Find the minimum value of , where .
-
21M.2.SL.TZ1.3c:
Write down the amount of the loan.
-
21M.2.SL.TZ1.3d.i:
the amount of interest paid by Daisy.
-
21M.2.SL.TZ1.3d.ii:
the annual interest rate of the loan.
-
21M.2.SL.TZ1.3e:
Find the amount of Daisy’s final payment.
-
21M.2.SL.TZ1.3f:
Find how much money Daisy saved by making one final payment after years.
-
21M.1.SL.TZ2.10a:
Calculate the amount Pietro will have in his account after years. Give your answer correct to decimal places.
-
21M.1.SL.TZ2.10b:
Tommaso wants to invest his money in an account such that his investment will increase to times the initial amount in years. Assume the account pays a nominal annual interest of compounded quarterly.
Determine the value of .
-
21M.1.AHL.TZ2.5a:
Estimate the value of Roger’s laptop after years.
-
21M.1.AHL.TZ2.5b:
Find the value of .
-
21M.1.AHL.TZ2.5c:
Comment on the validity of your answer to part (b).
-
21N.1.SL.TZ0.10a:
Find the amount they will pay the bank each month.
-
21N.1.SL.TZ0.10b.i:
Find the amount Raul and Rosy will still owe the bank at the end of the first years.
-
21N.1.SL.TZ0.10b.ii:
Using your answers to parts (a) and (b)(i), calculate how much interest they will have paid in total during the first years.
-
22M.1.SL.TZ2.13a:
For option 1, determine the minimum amount Juliana would need to invest. Give your answer to the nearest dollar.
-
22M.1.SL.TZ2.13b:
For option 2, find the minimum value of that Juliana would need to invest each year. Give your answer to the nearest dollar.
-
22M.2.SL.TZ2.2d.i:
Calculate the value of .
-
22M.2.SL.TZ2.2d.ii:
Describe what the value in part (d)(i) represents in this context.
SL 1.5—Intro to logs
-
SPM.1.SL.TZ0.8a:
An orchestra has a sound intensity of 6.4 × 10−3 W m−2 . Calculate the intensity level, of the orchestra.
-
SPM.1.SL.TZ0.8b:
A rock concert has an intensity level of 112 dB. Find the sound intensity, .
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
18M.1.AHL.TZ2.H_11b:
Express in terms of . Give your answer in the form , where p , q are constants.
-
18M.1.AHL.TZ2.H_11c:
The region R, is bounded by the graph of the function found in part (b), the x-axis, and the lines and where . The area of R is .
Find the value of .
-
18M.1.AHL.TZ1.H_5:
Solve .
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
17M.1.AHL.TZ1.H_1:
Find the solution of .
-
18M.1.SL.TZ2.S_7b:
Let and . Find the value of .
-
16N.1.SL.TZ0.S_9a:
Find .
-
16N.1.SL.TZ0.S_9b:
Show that the sum of the infinite sequence is .
-
16N.1.SL.TZ0.S_9c:
Find , giving your answer as an integer.
-
16N.1.SL.TZ0.S_9d:
Show that .
-
16N.1.SL.TZ0.S_9e:
Given that is equal to half the sum of the infinite geometric sequence, find , giving your answer in the form , where .
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
EXN.1.SL.TZ0.5a:
Find the value for a solution in which the hydrogen ion concentration is .
-
EXN.1.SL.TZ0.5b.i:
Write an expression for in terms of .
-
EXN.1.SL.TZ0.5b.ii:
Find the hydrogen ion concentration in a solution with . Give your answer in the form where and is an integer.
-
22M.1.SL.TZ1.11a:
Find the value of .
-
22M.1.SL.TZ1.11b:
Find the value of .
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.AHL.TZ1.12a:
Find the value of .
-
22M.1.AHL.TZ1.12b:
Find the value of .
-
22M.1.AHL.TZ1.12c:
Find the average number of earthquakes in a year with a magnitude of at least .
-
22M.1.SL.TZ2.4a:
Calculate the pH of the coffee.
-
22M.1.SL.TZ2.4b:
Determine whether the unknown liquid is more or less acidic than the coffee. Justify your answer mathematically.
SL 1.6—Approximating and estimating
-
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree. -
18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
-
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
-
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
-
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
Find the angle of elevation of A from D.
-
17N.2.SL.TZ0.T_3a:
Show that correct to the nearest metre.
-
17N.2.SL.TZ0.T_3b:
Calculate angle .
-
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
-
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
-
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
-
17M.2.SL.TZ1.T_1a:
Find the range of the average body weights for these seven species of mammal.
-
17M.2.SL.TZ1.T_1b.i:
For the data from these seven species calculate , the Pearson’s product–moment correlation coefficient;
-
17M.2.SL.TZ1.T_1b.ii:
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.
-
17M.2.SL.TZ1.T_1c:
Write down the equation of the regression line on , in the form .
-
17M.2.SL.TZ1.T_1d:
Use your regression line to estimate the average weight of the brain of grey wolves.
-
17M.2.SL.TZ1.T_1e:
Find the percentage error in your estimate in part (d).
-
17M.1.SL.TZ2.T_6a:
Write down the median length of these leaves.
-
17M.1.SL.TZ2.T_6b:
Write down the number of leaves with a length less than or equal to 8 cm.
-
16N.1.SL.TZ0.T_1c:
Write your answer to part (b)(ii) in the form , where .
-
18N.2.SL.TZ0.T_1a.ii:
Use your graphic display calculator to write down , the mean examination score.
-
18N.2.SL.TZ0.T_1a.iii:
Use your graphic display calculator to write down r , Pearson’s product–moment correlation coefficient.
-
18N.2.SL.TZ0.T_1b.i:
Find the exact value of m and of c for these data.
-
18N.2.SL.TZ0.T_1c.i:
Use the regression line y on x to estimate Jerome’s examination score.
-
18N.2.SL.TZ0.T_1c.ii:
Justify whether it is valid to use the regression line y on x to estimate Jerome’s examination score.
-
21M.1.SL.TZ1.1a:
Calculate Katya’s approximation of , correct to four decimal places.
-
21M.1.SL.TZ1.1b:
Calculate the percentage error in using Katya’s four decimal place approximation of , compared to the exact value of in your calculator.
-
21M.1.SL.TZ1.9:
A triangular field is such that and , each measured correct to the nearest metre, and the angle at is equal to , measured correct to the nearest .
Calculate the maximum possible area of the field.
-
21N.1.SL.TZ0.6a:
Use the trapezoidal rule with an interval width of to estimate the total amount of carbon dioxide emitted during these two hours.
-
21N.1.SL.TZ0.6b:
The real amount of carbon dioxide emitted during these two hours was tonnes.
Find the percentage error of the estimate found in part (a).
-
21N.2.SL.TZ0.2a:
Calculate the percentage increase in applications from the first year to the second year.
-
21N.2.SL.TZ0.2b.i:
Write down the common ratio of the sequence.
-
21N.2.SL.TZ0.2b.ii:
Find an expression for .
-
21N.2.SL.TZ0.2b.iii:
Find the number of student applications the university expects to receive when . Express your answer to the nearest integer.
-
21N.2.SL.TZ0.2c:
Write down an expression for .
-
21N.2.SL.TZ0.2d:
Calculate the total amount of acceptance fees paid to the university in the first years.
-
21N.2.SL.TZ0.2e:
Find .
-
21N.2.SL.TZ0.2f:
State whether, for all , the university will have places available for all applicants. Justify your answer.
-
22M.1.AHL.TZ2.8b:
Find the upper bound and lower bound of the area of the sector.
-
22M.1.AHL.TZ2.8c:
Find, with justification, the largest possible percentage error if the answer to part (a) is recorded as the area of the sector.
-
22M.2.SL.TZ1.1e:
Calculate the percentage error in the maximum number of daylight hours Boris recorded in the diagram.
SL 1.7—Loan repayments and amortization
-
SPM.2.SL.TZ0.1a.i:
Find the repayment made each quarter.
-
SPM.2.SL.TZ0.1a.ii:
Find the total amount paid for the car.
-
SPM.2.SL.TZ0.1a.iii:
Find the interest paid on the loan.
-
SPM.2.SL.TZ0.1b.i:
Find the amount to be borrowed for this option.
-
SPM.2.SL.TZ0.1b.ii:
Find the annual interest rate, .
-
SPM.2.SL.TZ0.1c:
State which option Bryan should choose. Justify your answer.
-
SPM.2.SL.TZ0.1d:
Bryan’s car depreciates at an annual rate of 25 % per year.
Find the value of Bryan’s car six years after it is purchased.
-
SPM.2.AHL.TZ0.3a.i:
Find the repayment made each quarter.
-
SPM.2.AHL.TZ0.3a.ii:
Find the total amount paid for the car.
-
SPM.2.AHL.TZ0.3a.iii:
Find the interest paid on the loan.
-
SPM.2.AHL.TZ0.3b.i:
Find the amount to be borrowed for this option.
-
SPM.2.AHL.TZ0.3b.ii:
Find the annual interest rate, .
-
SPM.2.AHL.TZ0.3c:
State which option Bryan should choose. Justify your answer.
-
SPM.2.AHL.TZ0.3d:
Bryan chooses option B. The car dealership invests the money Bryan pays as soon as they receive it.
If they invest it in an account paying 0.4 % interest per month and inflation is 0.1 % per month, calculate the real amount of money the car dealership has received by the end of the 6 year period.
-
EXM.2.SL.TZ0.1a.i:
the number of months it will take for Paul to repay the loan.
-
EXM.2.SL.TZ0.1a.ii:
the total amount that Paul has to pay.
-
EXM.2.SL.TZ0.1b.i:
the amount Paul pays each month.
-
EXM.2.SL.TZ0.1b.ii:
the total amount that Paul has to pay.
-
EXM.2.SL.TZ0.1c.i:
option 1.
-
EXM.2.SL.TZ0.1c.ii:
option 2.
-
EXM.2.SL.TZ0.2a.i:
Calculate the monthly repayment using option 1.
-
EXM.2.SL.TZ0.2a.ii:
Calculate the total amount Sophie would pay, using option 1.
-
EXM.2.SL.TZ0.2b.i:
Calculate the number of months it will take to repay the mortgage using option 2.
-
EXM.2.SL.TZ0.2b.ii:
Calculate the total amount Sophie would pay, using option 2.
-
EXM.2.SL.TZ0.2c.i:
option 1.
-
EXM.2.SL.TZ0.2c.ii:
option 2.
-
EXM.2.SL.TZ0.2d.i:
Use your answer to part (a)(i) to calculate the amount remaining on her mortgage after the first 10 years.
-
EXM.2.SL.TZ0.2d.ii:
Hence calculate her monthly repayment for the final 10 years.
-
EXM.1.SL.TZ0.6a:
Calculate the amount Yejin needs to have saved into her annuity fund, in order to meet her retirement goal.
-
EXM.1.SL.TZ0.6b:
Yejin has just turned 28 years old. She currently has no retirement savings. She wants to save part of her salary each month into her annuity fund.
Calculate the amount Yejin needs to save each month, to meet her retirement goal.
-
21N.1.SL.TZ0.10a:
Find the amount they will pay the bank each month.
-
21N.1.SL.TZ0.10b.i:
Find the amount Raul and Rosy will still owe the bank at the end of the first years.
-
21N.1.SL.TZ0.10b.ii:
Using your answers to parts (a) and (b)(i), calculate how much interest they will have paid in total during the first years.
-
22M.1.SL.TZ2.13a:
For option 1, determine the minimum amount Juliana would need to invest. Give your answer to the nearest dollar.
-
22M.1.SL.TZ2.13b:
For option 2, find the minimum value of that Juliana would need to invest each year. Give your answer to the nearest dollar.
SL 1.8—Use of technology to solve systems of linear equations and polynomial equations
-
SPM.1.AHL.TZ0.18:
The rate, , of a chemical reaction at a fixed temperature is related to the concentration of two compounds, and , by the equation
, where , , .
A scientist measures the three variables three times during the reaction and obtains the following values.
Find , and .
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
17N.2.AHL.TZ0.H_1:
Boxes of mixed fruit are on sale at a local supermarket.
Box A contains 2 bananas, 3 kiwifruit and 4 melons, and costs $6.58.
Box B contains 5 bananas, 2 kiwifruit and 8 melons and costs $12.32.
Box C contains 5 bananas and 4 kiwifruit and costs $3.00.
Find the cost of each type of fruit.
-
18N.1.AHL.TZ0.H_4a:
Find the value of for which the system of equations does not have a unique solution.
-
18N.1.AHL.TZ0.H_4b:
Find the solution of the system of equations when .
-
19M.2.SL.TZ2.T_4a.i:
Write down an equation, in terms of and , for the amount of the drug that she receives on the seventh day.
-
19M.2.SL.TZ2.T_4a.ii:
Write down an equation, in terms of and , for the amount of the drug that she receives on the eleventh day.
-
19M.2.SL.TZ2.T_4b:
Write down the value of and the value of .
-
19M.2.SL.TZ2.T_4c:
Calculate the total amount of the drug, in mg, that she receives.
-
19M.2.SL.TZ2.T_4d.i:
Find the amount of antibiotic, in mg, that Ted receives on the fifth day.
-
19M.2.SL.TZ2.T_4d.ii:
The daily amount of antibiotic Ted receives will first be less than 0.06 mg on the th day. Find the value of .
-
19M.2.SL.TZ2.T_4d.iii:
Hence find the total amount of antibiotic, in mg, that Ted receives during the first days.
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
22M.1.SL.TZ1.5a:
Write down three equations that express the information given above.
-
22M.1.SL.TZ1.5b:
Find the number of each type of ticket sold.
AHL 1.9—Log laws
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
18M.1.AHL.TZ2.H_11a:
Show that where .
-
18M.1.AHL.TZ2.H_11b:
Express in terms of . Give your answer in the form , where p , q are constants.
-
18M.1.AHL.TZ2.H_11c:
The region R, is bounded by the graph of the function found in part (b), the x-axis, and the lines and where . The area of R is .
Find the value of .
-
18M.1.AHL.TZ1.H_5:
Solve .
-
16N.1.AHL.TZ0.H_7:
Solve the equation .
-
17N.1.AHL.TZ0.H_1:
Solve the equation .
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
18M.1.SL.TZ2.S_7b:
Let and . Find the value of .
-
16N.1.SL.TZ0.S_9a:
Find .
-
16N.1.SL.TZ0.S_9b:
Show that the sum of the infinite sequence is .
-
16N.1.SL.TZ0.S_9c:
Find , giving your answer as an integer.
-
16N.1.SL.TZ0.S_9d:
Show that .
-
16N.1.SL.TZ0.S_9e:
Given that is equal to half the sum of the infinite geometric sequence, find , giving your answer in the form , where .
-
18M.2.SL.TZ1.S_8a:
Find the value of a and of b.
-
18M.2.SL.TZ1.S_8b:
Use the regression equation to estimate the value of y when x = 3.57.
-
18M.2.SL.TZ1.S_8c:
The relationship between x and y can be modelled using the formula y = kxn, where k ≠ 0 , n ≠ 0 , n ≠ 1.
By expressing ln y in terms of ln x, find the value of n and of k.
-
22M.2.AHL.TZ2.4c:
(i) the gradient of this line in terms of ;
(ii) the -intercept of this line in terms of .
-
22M.2.AHL.TZ2.4d:
Find the equation of the regression line for on .
AHL 1.10—Expressions with non-integer exponents
NoneAHL 1.11—Sum of infinite geometric sequences
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
20N.2.SL.TZ0.S_6a:
Find the common ratio in terms of .
-
20N.2.SL.TZ0.S_6b:
Find the values of for which the sum to infinity of the series exists.
-
20N.2.SL.TZ0.S_6c:
Find the value of when .
-
21M.1.AHL.TZ2.7a:
Find how high the balloon will travel in the first minutes after it is launched.
-
21M.1.AHL.TZ2.7b:
The balloon is required to reach a height of at least metres.
Determine whether it will reach this height. -
21M.1.AHL.TZ2.7c:
Suggest a limitation of the given model.
-
22M.1.AHL.TZ2.7:
The sum of an infinite geometric sequence is .
The first term is more than the second term.
Find the third term. Justify your answer.
AHL 1.12—Complex numbers introduction
-
EXM.2.AHL.TZ0.20a.ii:
Show that .
-
EXM.2.AHL.TZ0.20a.iii:
Hence find the value of .
-
EXM.2.AHL.TZ0.20c.i:
A3 = –I.
-
EXM.2.AHL.TZ0.20c.ii:
A–1 = I – A.
-
18M.1.AHL.TZ1.H_11a.i:
Express w2 and w3 in modulus-argument form.
-
EXN.1.AHL.TZ0.14a:
Write down in exponential form.
-
EXN.1.AHL.TZ0.14b:
An equilateral triangle is to be drawn on the Argand plane with one of the vertices at the point corresponding to and all the vertices equidistant from .
Find the points that correspond to the other two vertices. Give your answers in Cartesian form.
-
21M.1.AHL.TZ1.9a.i:
.
-
21M.1.AHL.TZ1.9a.ii:
.
-
21M.1.AHL.TZ1.9b:
Describe these two transformations and give the order in which they are applied.
-
21M.1.AHL.TZ1.9c:
Hence, or otherwise, find the value of when .
-
21N.2.AHL.TZ0.5a.i:
Plot the position of on an Argand Diagram.
-
21N.2.AHL.TZ0.5a.ii:
Express in the form , where , giving the exact value of and the exact value of .
-
21N.2.AHL.TZ0.5b.i:
Find in the form .
-
21N.2.AHL.TZ0.5b.ii:
Hence find in the form , where and .
-
21N.2.AHL.TZ0.5c.i:
Find the maximum value of .
-
21N.2.AHL.TZ0.5c.ii:
Find the phase shift of .
-
22M.1.AHL.TZ1.10a.i:
.
-
22M.1.AHL.TZ1.10a.ii:
.
-
22M.1.AHL.TZ1.10a.iii:
.
-
22M.1.AHL.TZ1.10b.i:
Find this value of .
-
22M.1.AHL.TZ1.10b.ii:
For this value of , plot the approximate position of on the Argand diagram.
-
22M.1.AHL.TZ2.13a:
Find an expression for in the form , where and are real constants.
-
22M.1.AHL.TZ2.13b:
Hence write down the maximum voltage in the circuit.
AHL 1.13—Polar and Euler form
-
SPM.1.AHL.TZ0.15a.i:
find the values of , , and .
-
SPM.1.AHL.TZ0.15a.ii:
draw , , , and on the following Argand diagram.
-
SPM.1.AHL.TZ0.15b:
Let .
Find the value of for which successive powers of lie on a circle.
-
18M.1.AHL.TZ1.H_11a.i:
Express w2 and w3 in modulus-argument form.
-
18M.1.AHL.TZ1.H_11a.ii:
Sketch on an Argand diagram the points represented by w0 , w1 , w2 and w3.
-
18M.1.AHL.TZ1.H_11b:
Show that the area of the quadrilateral Q is .
-
18M.1.AHL.TZ1.H_11c:
Let . The points represented on an Argand diagram by form the vertices of a polygon .
Show that the area of the polygon can be expressed in the form , where .
-
17M.1.AHL.TZ1.H_2a.i:
By expressing and in modulus-argument form write down the modulus of ;
-
17M.1.AHL.TZ1.H_2a.ii:
By expressing and in modulus-argument form write down the argument of .
-
17M.1.AHL.TZ1.H_2b:
Find the smallest positive integer value of , such that is a real number.
-
19M.2.AHL.TZ1.H_6a:
Show the points represented by and on the following Argand diagram.
-
17M.1.AHL.TZ2.H_11a:
Solve .
-
17M.1.AHL.TZ2.H_11b:
Show that .
-
17M.1.AHL.TZ2.H_11c.i:
Find the modulus and argument of in terms of . Express each answer in its simplest form.
-
17M.1.AHL.TZ2.H_11c.ii:
Hence find the cube roots of in modulus-argument form.
-
17M.1.AHL.TZ2.H_5:
In the following Argand diagram the point A represents the complex number and the point B represents the complex number . The shape of ABCD is a square. Determine the complex numbers represented by the points C and D.

-
EXN.1.AHL.TZ0.14a:
Write down in exponential form.
-
EXN.1.AHL.TZ0.14b:
An equilateral triangle is to be drawn on the Argand plane with one of the vertices at the point corresponding to and all the vertices equidistant from .
Find the points that correspond to the other two vertices. Give your answers in Cartesian form.
-
21M.1.AHL.TZ1.9a.i:
.
-
21M.1.AHL.TZ1.9a.ii:
.
-
21M.1.AHL.TZ1.9b:
Describe these two transformations and give the order in which they are applied.
-
21M.1.AHL.TZ1.9c:
Hence, or otherwise, find the value of when .
-
21M.3.AHL.TZ1.1h.i:
Write down and in exponential form, with a constant modulus.
-
21M.3.AHL.TZ1.1h.ii:
Hence or otherwise find an equation for in the form , where .
-
21M.3.AHL.TZ1.1h.iii:
Find, in hours, the shortest time from sunrise to sunset at point that is predicted by this model.
-
21M.1.AHL.TZ2.12a.i:
Find the value of .
-
21M.1.AHL.TZ2.12a.ii:
Find the value of for .
-
21M.1.AHL.TZ2.12b:
Find the least value of such that .
-
21N.2.AHL.TZ0.5a.i:
Plot the position of on an Argand Diagram.
-
21N.2.AHL.TZ0.5a.ii:
Express in the form , where , giving the exact value of and the exact value of .
-
21N.2.AHL.TZ0.5b.i:
Find in the form .
-
21N.2.AHL.TZ0.5b.ii:
Hence find in the form , where and .
-
21N.2.AHL.TZ0.5c.i:
Find the maximum value of .
-
21N.2.AHL.TZ0.5c.ii:
Find the phase shift of .
-
22M.1.AHL.TZ1.10a.i:
.
-
22M.1.AHL.TZ1.10a.ii:
.
-
22M.1.AHL.TZ1.10a.iii:
.
-
22M.1.AHL.TZ1.10b.i:
Find this value of .
-
22M.1.AHL.TZ1.10b.ii:
For this value of , plot the approximate position of on the Argand diagram.
-
22M.1.AHL.TZ2.13a:
Find an expression for in the form , where and are real constants.
-
22M.1.AHL.TZ2.13b:
Hence write down the maximum voltage in the circuit.
AHL 1.14—Introduction to matrices
-
EXM.2.AHL.TZ0.3a:
Find in terms of .
-
EXM.2.AHL.TZ0.3b:
If is equal to , find the value of .
-
EXM.2.AHL.TZ0.3c:
Using this value of , find and hence solve the system of equations:
-
EXM.1.AHL.TZ0.2:
If and det , find the possible values of .
-
EXM.1.AHL.TZ0.3:
and are 2 × 2 matrices, where and . Find
-
EXM.2.AHL.TZ0.4:
The matrices A, B, X are given by
A = , B = , X = , , , , .
Given that AX + X = Β, find the exact values of , , and .
-
EXM.1.AHL.TZ0.4a:
Write down the inverse, A–1.
-
EXM.1.AHL.TZ0.4b.i:
Given that XA + B = C, express X in terms of A–1, B and C.
-
EXM.1.AHL.TZ0.4b.ii:
Given that B , and C , find X.
-
EXM.2.AHL.TZ0.5a:
write down A + B.
-
EXM.2.AHL.TZ0.5b:
find AB.
-
EXM.1.AHL.TZ0.6a:
Find Q.
-
EXM.1.AHL.TZ0.6b:
Find CD.
-
EXM.1.AHL.TZ0.6c:
Find D–1.
-
EXM.2.AHL.TZ0.6a:
Write down A−1.
-
EXM.2.AHL.TZ0.6b:
Find D.
-
EXM.2.AHL.TZ0.6c:
Find X.
-
EXM.1.AHL.TZ0.7a.i:
Write down the value of .
-
EXM.1.AHL.TZ0.7a.ii:
Find the value of .
-
EXM.1.AHL.TZ0.7b:
Let .
Find the value of .
-
EXM.1.AHL.TZ0.8a:
Write down the inverse matrix A−1.
-
EXM.1.AHL.TZ0.8b.i:
Express X in terms of A−1 and B.
-
EXM.1.AHL.TZ0.8b.ii:
Hence, solve for X.
-
EXM.1.AHL.TZ0.9a.i:
Write down the value of .
-
EXM.1.AHL.TZ0.9a.ii:
Write down the value of .
-
EXM.1.AHL.TZ0.9b:
Write these equations as a matrix equation.
-
EXM.1.AHL.TZ0.9c:
Solve the matrix equation.
-
EXM.2.AHL.TZ0.7a.i:
Find 4.
-
EXM.2.AHL.TZ0.7a.ii:
Find 100.
-
EXM.2.AHL.TZ0.7b.i:
Find M2.
-
EXM.2.AHL.TZ0.7b.ii:
Show that M3 = .
-
EXM.2.AHL.TZ0.7c.i:
Write down M4.
-
EXM.2.AHL.TZ0.7c.ii:
Find T4.
-
EXM.2.AHL.TZ0.7d:
Using your results from part (a) (ii), find T100.
-
EXM.1.AHL.TZ0.10a:
2A − B.
-
EXM.1.AHL.TZ0.10b:
det (2A − B).
-
EXM.2.AHL.TZ0.8a:
Write down the value of .
-
EXM.2.AHL.TZ0.8b:
Show that .
-
EXM.2.AHL.TZ0.8c:
Write down the other two linear equations in , and .
-
EXM.2.AHL.TZ0.8d.i:
Write down these three equations as a matrix equation.
-
EXM.2.AHL.TZ0.8d.ii:
Solve this matrix equation.
-
EXM.2.AHL.TZ0.8e:
The function can also be written where and are integers. Find and .
-
EXM.2.AHL.TZ0.9a:
Write down the inverse of the matrix A = .
-
EXM.2.AHL.TZ0.9b:
Hence or otherwise solve
-
EXM.1.AHL.TZ0.22a:
Find AB.
-
EXM.1.AHL.TZ0.22b:
The matrix C = and 2AB = C. Find the value of .
-
EXM.1.AHL.TZ0.11a:
Find A + B.
-
EXM.1.AHL.TZ0.11b:
Find −3A.
-
EXM.1.AHL.TZ0.11c:
Find AB.
-
EXM.2.AHL.TZ0.10a.i:
Find A−1.
-
EXM.2.AHL.TZ0.10a.ii:
Find A2.
-
EXM.2.AHL.TZ0.10c:
Hence find A−1B.
-
EXM.2.AHL.TZ0.10d:
Let X be a 2 × 2 matrix such that AX = B. Find X.
-
EXM.2.AHL.TZ0.11a:
Write down the determinant of M.
-
EXM.2.AHL.TZ0.11b:
Write down M−1.
-
EXM.2.AHL.TZ0.11c:
Hence solve M.
-
EXM.1.AHL.TZ0.16a:
Find a relationship between and if the matrices and commute under matrix multiplication.
-
EXM.1.AHL.TZ0.16b.i:
Find the value of if the determinant of matrix is −1.
-
EXM.1.AHL.TZ0.16b.ii:
Write down for this value of .
-
EXM.2.AHL.TZ0.10b:
Given that 2A + B = , find the value of and of .
-
EXM.2.AHL.TZ0.20a.ii:
Show that .
-
EXM.2.AHL.TZ0.20a.iii:
Hence find the value of .
-
EXM.2.AHL.TZ0.20c.i:
A3 = –I.
-
EXM.2.AHL.TZ0.20c.ii:
A–1 = I – A.
-
EXM.2.AHL.TZ0.21a.i:
find X and Y.
-
EXM.2.AHL.TZ0.21a.ii:
does X–1 + Y–1 have an inverse? Justify your conclusion.
-
EXM.2.AHL.TZ0.21b.i:
find and in terms of .
-
EXM.2.AHL.TZ0.21b.ii:
and hence find an expression for .
-
EXM.2.AHL.TZ0.22a.i:
Show that .
-
EXM.2.AHL.TZ0.22a.ii:
Find an expression for in terms of .
-
EXM.2.AHL.TZ0.22b:
Hence show that M is a singular matrix.
-
EXM.2.AHL.TZ0.22c:
If all of the elements of M are positive, find the range of possible values for .
-
EXM.2.AHL.TZ0.22d:
Show that (I − M)2 = I − M where I is the identity matrix.
-
EXM.1.AHL.TZ0.25a:
Find the matrix A2.
-
EXM.1.AHL.TZ0.25b:
If det A2 = 16, determine the possible values of .
-
EXM.1.AHL.TZ0.26a:
Find BA.
-
EXM.1.AHL.TZ0.26b:
Calculate det (BA).
-
EXM.1.AHL.TZ0.26c:
Find A(A–1B + 2A–1)A.
-
EXM.1.AHL.TZ0.27a:
(A + B)2 = A2 + 2AB + B2
-
EXM.1.AHL.TZ0.27b:
(A – kI)3 = A3 – 3kA2 + 3k2A – k3
-
EXM.1.AHL.TZ0.27c:
CA = B C =
-
EXM.1.AHL.TZ0.28:
Consider the matrix A , where .
Find the value of for which A is singular.
-
EXM.1.AHL.TZ0.29a:
Show that M is non-singular.
-
EXM.1.AHL.TZ0.29b:
Calculate M2.
-
EXM.1.AHL.TZ0.29c:
Show that det(M2) is positive.
-
EXM.1.AHL.TZ0.30a:
Given that AB = , find .
-
EXM.1.AHL.TZ0.30b:
Hence, or otherwise, find A–1.
-
EXM.1.AHL.TZ0.30c:
Find the matrix X, such that AX = C.
-
EXM.1.AHL.TZ0.31:
Find the determinant of A, where A = .
-
EXM.1.AHL.TZ0.32:
If A = and A2 is a matrix whose entries are all 0, find .
-
EXM.1.AHL.TZ0.33:
Given that M = and that M2 – 6M + kI = 0 find k.
-
EXM.1.AHL.TZ0.34:
The square matrix X is such that X3 = 0. Show that the inverse of the matrix (I – X) is I + X + X2.
-
EXM.1.AHL.TZ0.35a:
Write down the inverse of the matrix
A =
-
EXM.1.AHL.TZ0.35b:
Hence, find the point of intersection of the three planes.
-
EXM.1.AHL.TZ0.35c:
A fourth plane with equation passes through the point of intersection. Find the value of .
-
EXM.1.AHL.TZ0.43a:
Find the values of and given that the matrix is the inverse of the matrix .
-
EXM.1.AHL.TZ0.43b:
For the values of and found in part (a), solve the system of linear equations
-
EXM.1.AHL.TZ0.44:
Find the values of the real number for which the determinant of the matrix is equal to zero.
-
EXM.1.AHL.TZ0.45a:
Given matrices A, B, C for which AB = C and det A ≠ 0, express B in terms of A and C.
-
EXM.1.AHL.TZ0.45b.i:
Find the matrix DA.
-
EXM.1.AHL.TZ0.45b.ii:
Find B if AB = C.
-
EXM.1.AHL.TZ0.45c:
Find the coordinates of the point of intersection of the planes , , .
-
EXM.1.AHL.TZ0.46:
If A = and B = , find 2 values of and , given that AB = BA.
-
EXM.1.AHL.TZ0.48:
The matrices A, B, C and X are all non-singular 3 × 3 matrices.
Given that A–1XB = C, express X in terms of the other matrices.
-
EXM.1.AHL.TZ0.49:
The square matrix X is such that X3 = 0. Show that the inverse of the matrix (I – X) is I + X + X2.
-
EXM.1.AHL.TZ0.50:
Given that A = and B = , find X if BX = A – AB.
-
EXM.1.AHL.TZ0.52a:
Find the inverse of the matrix .
-
EXM.1.AHL.TZ0.52b:
Hence solve the system of equations
-
EXM.1.AHL.TZ0.54a:
Find det A.
-
EXM.1.AHL.TZ0.54b:
Find the set of values of for which the system has a unique solution.
-
EXM.2.AHL.TZ0.23a:
Find the values of for which the matrix (A − I) is singular.
-
EXM.2.AHL.TZ0.23b.i:
Find the value of and of .
-
EXM.2.AHL.TZ0.23b.ii:
Hence show that I = A (6I – A).
-
EXM.2.AHL.TZ0.23b.iii:
Use the result from part (b) (ii) to explain why A is non-singular.
-
EXM.2.AHL.TZ0.23c:
Use the values from part (b) (i) to express A4 in the form A+ I where , .
-
19M.2.AHL.TZ0.F_3a:
Given that M3 can be written as a quadratic expression in M in the form aM2 + bM + cI , determine the values of the constants a, b and c.
-
19M.2.AHL.TZ0.F_3b:
Show that M4 = 19M2 + 40M + 30I.
-
19M.2.AHL.TZ0.F_3c:
Using mathematical induction, prove that Mn can be written as a quadratic expression in M for all positive integers n ≥ 3.
-
19M.2.AHL.TZ0.F_3d:
Find a quadratic expression in M for the inverse matrix M–1.
-
18M.1.AHL.TZ0.F_2a:
Show that A4 = 12A + 5I.
-
18M.1.AHL.TZ0.F_2b:
Let B = .
Given that B2 – B – 4I = , find the value of .
-
19M.1.AHL.TZ0.F_13a:
Given that A is non-singular, prove that f is a bijection.
-
19M.1.AHL.TZ0.F_13b:
It is now given that A is singular.
By considering appropriate determinants, prove that f is not a bijection.
-
20N.1.AHL.TZ0.F_4a:
By considering the determinant of a relevant matrix, show that the eigenvalues, , of satisfy the equation
,
where and are functions of to be determined.
-
20N.1.AHL.TZ0.F_4b.i:
Verify that
0.
-
20N.1.AHL.TZ0.F_4b.ii:
Assuming that is non-singular, use the result in part (b)(i) to show that
.
-
21N.2.AHL.TZ0.4a.i:
Write down each of the transformations in matrix form, clearly stating which matrix represents each transformation.
-
21N.2.AHL.TZ0.4a.ii:
Find a single matrix that defines a transformation that represents the overall change in position.
-
21N.2.AHL.TZ0.4a.iii:
Find .
-
21N.2.AHL.TZ0.4a.iv:
Hence state what the value of indicates for the possible movement of the drone.
-
21N.2.AHL.TZ0.4b:
Three drones are initially positioned at the points , and . After performing the movements listed above, the drones are positioned at points , and respectively.
Show that the area of triangle is equal to the area of triangle .
-
21N.2.AHL.TZ0.4c:
Find a single transformation that is equivalent to the three transformations represented by matrix .
-
22M.1.AHL.TZ2.15b:
Find the value of .
-
22M.2.AHL.TZ1.7a.i:
By considering the image of , find .
-
22M.2.AHL.TZ1.7a.ii:
By considering the image of and , show that
.
-
22M.2.AHL.TZ1.7b:
Write down the matrix .
-
22M.2.AHL.TZ1.7c.i:
Use to find the matrix .
-
22M.2.AHL.TZ1.7c.ii:
Hence find the angle and direction of the rotation represented by .
-
22M.2.AHL.TZ1.7d.i:
Write down an equation satisfied by .
-
22M.2.AHL.TZ1.7d.ii:
Find the value of and the value of .
AHL 1.15—Eigenvalues and eigenvectors
-
EXM.3.AHL.TZ0.5a:
Find the eigenvalues for . For each eigenvalue find the set of associated eigenvectors.
-
EXM.3.AHL.TZ0.5b:
Show that the matrix equation is equivalent to the Cartesian equation .
-
EXM.3.AHL.TZ0.5c.i:
Show that and are unit eigenvectors and that they correspond to different eigenvalues.
-
EXM.3.AHL.TZ0.5d.i:
Find matrix R.
-
EXM.3.AHL.TZ0.5d.ii:
Show that .
-
EXM.3.AHL.TZ0.5e.i:
Verify that .
-
EXM.3.AHL.TZ0.5e.ii:
Hence, find the Cartesian equation satisfied by and .
-
EXM.3.AHL.TZ0.5c.ii:
Hence, show that .
-
EXM.3.AHL.TZ0.5f:
Find the Cartesian equation satisfied by and and state the geometric shape that this curve represents.
-
EXM.3.AHL.TZ0.5g:
State geometrically what transformation the matrix represents.
-
EXM.3.AHL.TZ0.5h.i:
the curve in and in part (e) (ii), giving a reason.
-
EXM.3.AHL.TZ0.5h.ii:
the curve in and in part (b).
-
EXM.3.AHL.TZ0.5i:
Write down the equations of two lines of symmetry for the curve in and in part (b).
-
EXM.1.AHL.TZ0.42:
Given the matrix A = find the values of the real number for which where
-
EXM.1.AHL.TZ0.47:
Given that A = and I = , find the values of for which (A – I) is a singular matrix.
-
EXM.2.AHL.TZ0.23a:
Find the values of for which the matrix (A − I) is singular.
-
EXM.2.AHL.TZ0.23b.i:
Find the value of and of .
-
EXM.2.AHL.TZ0.23b.ii:
Hence show that I = A (6I – A).
-
EXM.2.AHL.TZ0.23b.iii:
Use the result from part (b) (ii) to explain why A is non-singular.
-
EXM.2.AHL.TZ0.23c:
Use the values from part (b) (i) to express A4 in the form A+ I where , .
-
19M.1.AHL.TZ0.F_3a.i:
Show that the eigenvalues of A are real if .
-
19M.1.AHL.TZ0.F_3a.ii:
Deduce that the eigenvalues are real if A is symmetric.
-
19M.1.AHL.TZ0.F_3b.i:
Determine the eigenvalues of B.
-
19M.1.AHL.TZ0.F_3b.ii:
Determine the corresponding eigenvectors.
-
20N.1.AHL.TZ0.F_4a:
By considering the determinant of a relevant matrix, show that the eigenvalues, , of satisfy the equation
,
where and are functions of to be determined.
-
20N.1.AHL.TZ0.F_4b.i:
Verify that
0.
-
20N.1.AHL.TZ0.F_4b.ii:
Assuming that is non-singular, use the result in part (b)(i) to show that
.
-
EXN.2.AHL.TZ0.5a.i:
the eigenvalues.
-
EXN.2.AHL.TZ0.5a.ii:
the eigenvectors.
-
EXN.2.AHL.TZ0.5b:
Hence write down the general solution of the system of equations.
-
EXN.2.AHL.TZ0.5c:
Sketch the phase portrait for this system, for .
On your sketch show
- the equation of the line defined by the eigenvector in the first quadrant
- at least two trajectories either side of this line using arrows on those trajectories to represent the change in populations as t increases
-
EXN.2.AHL.TZ0.5d:
Write down a condition on the size of the initial population of if it is to avoid its population reducing to zero.
-
EXN.2.AHL.TZ0.5e.i:
Find the value of at which .
-
EXN.2.AHL.TZ0.5e.ii:
Find the population of at this value of . Give your answer to the nearest herbivores.
-
21M.2.AHL.TZ1.5a:
It is sunny today. Find the probability that it will be sunny in three days’ time.
-
21M.2.AHL.TZ1.5b:
Find the eigenvalues and eigenvectors of .
-
21M.2.AHL.TZ1.5c.i:
Write down the matrix .
-
21M.2.AHL.TZ1.5c.ii:
Write down the matrix .
-
21M.2.AHL.TZ1.5d:
Hence find the long-term percentage of sunny days in Vokram.
-
21M.2.AHL.TZ2.4a:
Write down a transition matrix indicating the annual population movement between clinics.
-
21M.2.AHL.TZ2.4b:
Find a prediction for the ratio of the number of patients Doctor Black will have, compared to Doctor Green, after two years.
-
21M.2.AHL.TZ2.4c:
Find a matrix , with integer elements, such that , where is a diagonal matrix.
-
21M.2.AHL.TZ2.4d:
Hence, show that the long-term transition matrix is given by .
-
21M.2.AHL.TZ2.4e:
Hence, or otherwise, determine the expected ratio of the number of patients Doctor Black would have compared to Doctor Green in the long term.
-
21M.2.AHL.TZ2.7a:
Find the eigenvalues and corresponding eigenvectors of the matrix .
-
21M.2.AHL.TZ2.7b:
Hence, write down the general solution of the system.
-
21M.2.AHL.TZ2.7c:
Determine, with justification, whether the equilibrium point is stable or unstable.
-
21M.2.AHL.TZ2.7d:
(i) at .
(ii) at .
-
21M.2.AHL.TZ2.7e:
Sketch a phase portrait for the general solution to the system of coupled differential equations for , .
-
21N.2.AHL.TZ0.6a:
Given that , show that .
-
21N.2.AHL.TZ0.6b:
Write down the matrix .
-
21N.2.AHL.TZ0.6c.i:
Find the eigenvalues of matrix .
-
21N.2.AHL.TZ0.6c.ii:
Find the eigenvectors of matrix .
-
21N.2.AHL.TZ0.6d:
Given that when the shock absorber is displaced and its velocity is zero, find an expression for in terms of .
-
22M.1.AHL.TZ1.11a:
Find an eigenvector corresponding to the eigenvalue of . Give your answer in the form , where .
-
22M.2.AHL.TZ1.4a.i:
Use the substitution to show that this equation can be written as
.
-
22M.2.AHL.TZ1.4a.ii:
Find the eigenvalues for the matrix .
-
22M.2.AHL.TZ1.4a.iii:
Hence state the long-term velocity of the particle.
-
22M.2.AHL.TZ2.5b:
Find the eigenvalues of .
-
22M.2.AHL.TZ2.5c:
Find the eigenvectors of .
-
22M.2.AHL.TZ2.7b:
Find the eigenvalues of the system of coupled first order equations given in part (a).
