| Date | November Example question | Marks available | 1 | Reference code | EXN.3.AHL.TZ0.2 |
| Level | Additional Higher Level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | State | Question number | 2 | Adapted from | N/A |
Question
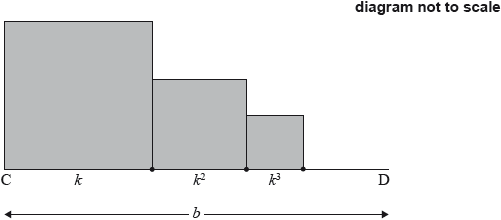
A graphic designer, Ben, wants to create an animation in which a sequence of squares is created by a composition of successive enlargements and translations and then rotated about the origin and reduced in size.
Ben outlines his plan with the following storyboards.
The first four frames of the animation are shown below in greater detail.
The sides of each successive square are one half the size of the adjacent larger square. Let the sequence of squares be
The first square, , has sides of length .
Ben decides the animation will continue as long as the width of the square is greater than the width of one pixel.
Ben decides to generate the squares using the transformation
where is a matrix that represents an enlargement, is a column vector that represents a translation, is a point in and is its image in .
By considering the case where is ,
Once the image of squares has been produced, Ben wants to continue the animation by rotating the image counter clockwise about the origin and having it reduce in size during the rotation.
Let be the enlargement matrix used when the original sequence of squares has been rotated through degrees.
Ben decides the enlargement scale factor, , should be a linear function of the angle, , and after a rotation of the sequence of squares should be half of its original length.
Find an expression for the width of in centimetres.
Given the width of a pixel is approximately , find the number of squares in the final image.
Write down .
Write down , in terms of .
state the coordinates, , of its image in .
hence find .
show that .
Hence or otherwise, find the coordinates of the top left-hand corner in .
Find, , in the form .
Write down .
Hence find the image of after it is rotated and enlarged.
Find the value of at which the enlargement scale factor equals zero.
After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.
Describe the animation for these two revolutions, stating the final position of the sequence of squares.
Markscheme
* This sample question was produced by experienced DP mathematics senior examiners to aid teachers in preparing for external assessment in the new MAA course. There may be minor differences in formatting compared to formal exam papers.
M1A1
[2 marks]
(A1)
(A1)
Note: Accept equations in place of inequalities.
Hence there are squares A1
[3 marks]
A1
[1 mark]
A1
[1 mark]
A1
[1 mark]
(M1)
A1
[2 marks]
Recognise the geometric series M1
Each component is equal to M1A1
AG
[3 marks]
M1A1
A1
[3 marks]
M1A1
A1
A1
[4 marks]
A1
[1 mark]
M1A1A1
A1
[4 marks]
A1
[1 mark]
The image will expand from zero (accept equivalent answers)
It will rotate counter clockwise
The design will (re)appear in the opposite (third) quadrant A1A1
Note: Accept any two of the above
Its final position will be in the opposite (third) quadrant or from its original position or equivalent statement. A1
[3 marks]