| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.SL.TZ2.T_9 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 2 |
| Command term | Write down | Question number | T_9 | Adapted from | N/A |
Question
Consider the geometric sequence .
Write down the common ratio of the sequence.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1) (C1)
[1 mark]
Examiners report
Syllabus sections
-
22M.2.SL.TZ2.2d.i:
Calculate the value of .
-
17N.2.SL.TZ0.T_2a.i:
Write down the distance Rosa runs in the third training session;
-
18M.2.SL.TZ2.T_4d:
Calculate the tea-shop’s total profit for the first 12 weeks.
-
EXN.3.AHL.TZ0.2d.i:
state the coordinates, , of its image in .
-
22M.1.SL.TZ1.13c:
Find the total vertical distance travelled by the ball from the point at which it is dropped until the fourth bounce.
-
22M.2.SL.TZ2.2d.ii:
Describe what the value in part (d)(i) represents in this context.
-
20N.1.SL.TZ0.T_15c:
The apple pie has a volume of .
Find the total number of slices Mia can cut from this pie.
-
22M.1.SL.TZ1.13a:
Show that the maximum height reached by the ball after it has bounced for the sixth time is , to the nearest .
-
21N.2.SL.TZ0.2f:
State whether, for all , the university will have places available for all applicants. Justify your answer.
-
EXN.3.AHL.TZ0.2f.ii:
Write down .
-
22M.1.AHL.TZ2.7:
The sum of an infinite geometric sequence is .
The first term is more than the second term.
Find the third term. Justify your answer.
-
21N.1.AHL.TZ0.6b:
Find the least value of such that .
-
22M.1.SL.TZ1.13b:
Find the number of times, after the first bounce, that the maximum height reached is greater than .
-
21N.2.SL.TZ0.2b.i:
Write down the common ratio of the sequence.
-
18M.2.SL.TZ2.T_4c:
Find the tea-shop’s profit during the 11th week.
-
18M.2.SL.TZ2.T_4e:
In the mth week the tea-shop’s total profit exceeds the café’s total profit, for the first time since they both opened.
Find the value of m.
-
18M.2.SL.TZ2.T_4b:
Calculate the café’s total profit for the first 12 weeks.
-
17M.1.SL.TZ1.S_7a:
Find the common ratio.
-
19M.2.AHL.TZ1.H_11a:
Show that .
-
19M.2.SL.TZ2.T_4d.iii:
Hence find the total amount of antibiotic, in mg, that Ted receives during the first days.
-
19M.2.SL.TZ2.T_4b:
Write down the value of and the value of .
-
17N.2.SL.TZ0.T_2a.ii:
Write down the distance Rosa runs in the th training session.
-
19N.1.SL.TZ0.T_7a:
Find the common ratio.
-
18N.2.AHL.TZ0.H_1b:
Find the sum to infinity of this sequence.
-
19M.2.SL.TZ1.T_5c:
Calculate, in years, when the bicycle value will be less than 50 USD.
-
18N.2.AHL.TZ0.H_1a:
Find the common ratio of this sequence.
-
19M.2.AHL.TZ1.H_11b:
Show that one of the real roots is equal to 1.
-
17N.2.SL.TZ0.T_2b:
Find the value of .
-
18M.2.SL.TZ2.S_4a:
Find the common ratio.
-
19M.2.SL.TZ1.T_5a:
Calculate, in CAD, the total amount John pays for the bicycle.
-
17N.2.SL.TZ0.T_2d:
Find the distance Carlos runs in the fifth month of training.
-
19M.2.SL.TZ2.T_4a.i:
Write down an equation, in terms of and , for the amount of the drug that she receives on the seventh day.
-
EXN.3.AHL.TZ0.2g:
Find the value of at which the enlargement scale factor equals zero.
-
19M.2.SL.TZ2.T_4d.ii:
The daily amount of antibiotic Ted receives will first be less than 0.06 mg on the th day. Find the value of .
-
18M.2.SL.TZ2.S_4b:
Find the sum of the first 8 terms.
-
19M.2.SL.TZ2.T_4d.i:
Find the amount of antibiotic, in mg, that Ted receives on the fifth day.
-
19N.1.SL.TZ0.T_7c:
The sum of the first terms is greater than .
Find the smallest possible value of .
-
18M.2.SL.TZ2.T_4a:
Find the café’s profit during the 11th week.
-
17N.2.SL.TZ0.T_2e:
Calculate the total distance Carlos runs in the first year.
-
18M.2.SL.TZ2.S_4c:
Find the least value of n for which Sn > 163.
-
17N.1.SL.TZ0.S_10a:
The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are , where .
Show that .
-
19M.2.SL.TZ2.T_4c:
Calculate the total amount of the drug, in mg, that she receives.
-
20N.1.SL.TZ0.T_15b:
Find the volume of the smallest slice of pie.
-
20N.1.SL.TZ0.T_15a:
Find the common ratio of the sequence.
-
21M.1.SL.TZ1.8a.i:
Charlie ran on day of his fitness programme.
-
19N.1.SL.TZ0.T_7b:
Write down the second term of this sequence.
-
21M.1.AHL.TZ2.7a:
Find how high the balloon will travel in the first minutes after it is launched.
-
21M.1.AHL.TZ2.7c:
Suggest a limitation of the given model.
-
21M.2.SL.TZ2.3b:
Find the average number of visitors per concert in .
-
21M.2.SL.TZ2.3d:
It is assumed that the concert hall will host concerts each year.
Use the average number of visitors per concert per year to predict the total number of people expected to attend the concert hall from when it opens until the end of .
-
19M.2.SL.TZ2.T_4a.ii:
Write down an equation, in terms of and , for the amount of the drug that she receives on the eleventh day.
-
19M.2.SL.TZ1.T_5d:
Find the total amount John has paid to insure his bicycle for the first 5 years.
-
17M.2.SL.TZ2.S_5:
Consider a geometric sequence where the first term is 768 and the second term is 576.
Find the least value of such that the th term of the sequence is less than 7.
-
17N.2.SL.TZ0.T_2c:
Calculate the total distance, in kilometres, Rosa runs in the first 50 training sessions.
-
EXN.3.AHL.TZ0.2d.ii:
hence find .
-
19M.2.SL.TZ1.T_5b:
Find the value of the bicycle during the 5th year. Give your answer to two decimal places.
-
17N.1.SL.TZ0.S_10b:
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.
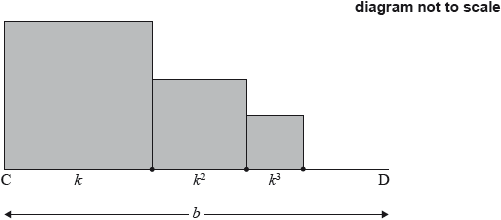
The total sum of the areas of all the squares is . Find the value of .
-
19M.2.AHL.TZ1.H_11c:
Given that , find the other two real roots.
-
21M.1.SL.TZ1.8a.ii:
Daniella ran on day of her fitness programme.
-
21M.1.AHL.TZ2.7b:
The balloon is required to reach a height of at least metres.
Determine whether it will reach this height. -
21N.1.AHL.TZ0.6a:
Find the common ratio, , for the sequence.
-
EXN.3.AHL.TZ0.2h:
After the enlargement scale factor equals zero, Ben continues to rotate the image for another two revolutions.
Describe the animation for these two revolutions, stating the final position of the sequence of squares.
-
EXN.3.AHL.TZ0.2f.iii:
Hence find the image of after it is rotated and enlarged.
-
EXN.3.AHL.TZ0.2d.iii:
show that .
-
EXN.3.AHL.TZ0.2e:
Hence or otherwise, find the coordinates of the top left-hand corner in .
-
EXN.3.AHL.TZ0.2f.i:
Find, , in the form .
-
21N.2.SL.TZ0.2a:
Calculate the percentage increase in applications from the first year to the second year.
-
21N.2.SL.TZ0.2b.ii:
Find an expression for .
-
21N.2.SL.TZ0.2b.iii:
Find the number of student applications the university expects to receive when . Express your answer to the nearest integer.
-
21N.2.SL.TZ0.2c:
Write down an expression for .
-
21N.2.SL.TZ0.2d:
Calculate the total amount of acceptance fees paid to the university in the first years.
-
21N.2.SL.TZ0.2e:
Find .

