| Date | November 2017 | Marks available | 9 | Reference code | 17N.1.SL.TZ0.S_10 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Find | Question number | S_10 | Adapted from | N/A |
Question
The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are , where .
Show that .
The following diagram shows [CD], with length , where . Squares with side lengths , where , are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.
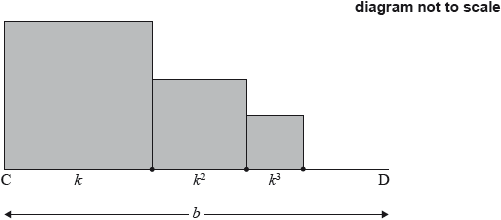
The total sum of the areas of all the squares is . Find the value of .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
infinite sum of segments is 2 (seen anywhere) (A1)
eg
recognizing GP (M1)
egratio is
correct substitution into formula (may be seen in equation) A1
eg
correct equation (A1)
eg
correct working leading to answer A1
eg
AG N0
[5 marks]
recognizing infinite geometric series with squares (M1)
eg
correct substitution into (must substitute into formula) (A2)
eg
correct working (A1)
eg
(seen anywhere) A1
valid approach with segments and CD (may be seen earlier) (M1)
eg
correct expression for in terms of (may be seen earlier) (A1)
eg
substituting their value of into their formula for (M1)
eg
A1 N3
[9 marks]

