DP Mathematics: Applications and Interpretation Questionbank

Topic 2—Functions
| Path: |
Description
[N/A]Directly related questions
-
20N.2.SL.TZ0.S_4a:
Find .
-
20N.2.SL.TZ0.S_8b:
Find .
-
EXN.1.SL.TZ0.2a:
Find an equation which links and .
-
EXN.2.SL.TZ0.3b.ii:
Hence write down the domain of .
-
21M.1.SL.TZ1.4c:
The price of gas at Erica’s gas station is per litre. A customer must buy a minimum of litres of gas. The total cost at Erica’s gas station is cheaper than Leon’s gas station when .
Find the minimum value of .
-
21M.1.SL.TZ1.8b:
On day of the fitness programmes Daniella runs more than Charlie for the first time.
Find the value of .
-
21M.1.SL.TZ1.11a:
Show that .
-
21M.1.SL.TZ1.11c:
Whilst swimming, Scarlett can hear the siren only if the sound intensity at her location is greater than .
Find the values of where Scarlett cannot hear the siren.
-
21M.1.SL.TZ2.12b:
Find the value of
(i) .
(ii) .
(iii) .
-
21M.2.SL.TZ1.5c.ii:
Hence find the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2a.ii:
Hence find the maximum height of the tunnel.
-
21M.2.AHL.TZ1.4b.i:
Find the equation of the least squares regression quadratic curve for these four points.
-
21N.1.SL.TZ0.5a:
Find the range of .
-
21N.1.AHL.TZ0.12a:
Use the data in the second table to find the value of and the value of for the regression line, .
-
21N.1.AHL.TZ0.10a:
Find .
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.AHL.TZ0.2f:
The wind speed increases and the blades rotate faster, but still at a constant rate.
Given that point is now higher than for second during each complete rotation, find the time for one complete rotation.
-
21N.2.AHL.TZ0.2e.i:
Find the height of above the ground when .
-
22M.1.SL.TZ1.3b:
Find the value of when the ball hits the ground.
-
22M.1.SL.TZ1.5b:
Find the number of each type of ticket sold.
-
22M.1.SL.TZ2.9b.ii:
Write down three simultaneous equations for and .
-
SPM.1.AHL.TZ0.14a.ii:
Find the value of .
-
SPM.2.SL.TZ0.5g:
It is found that once a driver realizes the need to stop their vehicle, 1.6 seconds will elapse, on average, before the brakes are engaged. During this reaction time, the vehicle will continue to travel at its original speed.
A truck approaches an intersection with speed . The driver notices the intersection’s traffic lights are red and they must stop the vehicle within a distance of .
Using model B and taking reaction time into account, calculate the maximum possible speed of the truck if it is to stop before the intersection.
-
22M.2.SL.TZ2.4b:
Calculate the number of revolutions of the Ferris wheel per ride.
-
22M.3.AHL.TZ1.1d:
Find in which city, X or Y, the computer virus is spreading more easily. Justify your answer using your results from part (b).
-
22M.2.SL.TZ2.5e:
Determine the maximum amount of coffee the cafe can make that will not result in a loss of money for the morning.
-
EXM.2.SL.TZ0.3c:
Solve this system of three equations to find the value of , and .
-
EXM.2.SL.TZ0.3a:
Show that .
-
22M.2.AHL.TZ2.4b:
Given that and , sketch the graph of against .
-
EXM.3.AHL.TZ0.7d.i:
Show that .
-
EXM.3.AHL.TZ0.7d.iii:
By finding the equation of a suitable regression line, show that and .
-
EXM.3.AHL.TZ0.9f.ii:
.
-
22M.3.AHL.TZ1.1b.v:
By considering large values of write down one criticism of the model found in (b)(ii).
-
17N.1.SL.TZ0.T_11c:
Find the value of and of .
-
16N.2.SL.TZ0.T_1c:
Plot the point on your scatter diagram and label this point M.
-
17N.1.SL.TZ0.T_15b:
Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.
-
17N.1.SL.TZ0.T_15c:
Write down an expression for in terms of .
-
17N.1.SL.TZ0.T_6c:
Find the value of and of .
-
17N.2.SL.TZ0.T_5c:
Use your answer to part (b)(ii) to find the values of for which is increasing.
-
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
-
19M.2.SL.TZ2.T_5d:
Find .
-
18N.1.SL.TZ0.S_8d:
The graph of a second function, , is obtained by a reflection of the graph of in the -axis, followed by a translation of .
Find the coordinates of the vertex of the graph of .
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18M.1.SL.TZ1.S_4a.i:
The equation of the axis of symmetry is x = p. Find p.
-
17N.1.SL.TZ0.T_12a:
Write down what the value of 150 represents in the context of the question.
-
17M.2.SL.TZ2.S_4a:
Find the value of .
-
16N.1.SL.TZ0.T_9b:
Find the value of .
-
18M.1.SL.TZ1.T_9a.i:
Find the number of fruit flies which were placed in the container.
-
18M.1.SL.TZ2.T_10b:
Interpret what A represents in this context.
-
19M.1.SL.TZ2.S_4a.i:
Find the -intercept of the graph of .
-
17M.2.SL.TZ1.T_4a:
Calculate the volume of this pan.
-
17M.2.SL.TZ1.T_4e:
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
-
17N.1.SL.TZ0.T_14a:
Write down the derivative of .
-
18M.2.SL.TZ2.T_6d:
Find .
-
19M.1.SL.TZ2.S_4c:
Describe the transformation .
-
19M.1.AHL.TZ1.H_10a.i:
Find the remainder when is divided by .
-
17M.2.SL.TZ1.T_3d:
Write down the coordinates of the -intercept.
-
17M.2.SL.TZ1.T_3f:
Find the solution of .
-
17M.1.SL.TZ2.T_14b:
Use your graphic display calculator to find how long it will take for Jashanti to have saved enough money to buy the car.
-
18M.1.AHL.TZ2.H_10a:
Find the inverse function , stating its domain.
-
18M.1.AHL.TZ2.H_10b.ii:
Sketch the graph of . State the equations of any asymptotes and the coordinates of any intercepts with the axes.
-
18M.2.AHL.TZ2.H_10a.i:
Sketch the graph of for .
-
18M.2.AHL.TZ2.H_10a.ii:
With reference to your graph, explain why is a function on the given domain.
-
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to .
-
17M.2.SL.TZ2.S_6a:
Show that .
-
17M.2.SL.TZ2.S_6c:
The equation has exactly two solutions, for . Find the possible values of .
-
17M.2.SL.TZ1.T_6a:
Find .
-
17M.2.SL.TZ1.T_6b.i:
Show that .
-
17M.2.SL.TZ1.T_6c:
Use your answer to part (a) and the value of , to find the -coordinates of the stationary points of the graph of .
-
19N.2.SL.TZ0.T_2c:
Find the equation of . Give your answer in the form , where .
-
19N.2.SL.TZ0.T_4b:
Write down the equation for the axis of symmetry of the graph.
-
17M.2.SL.TZ1.S_8b.ii:
Find the value of ;
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
17M.2.SL.TZ1.S_8a.ii:
Find the difference in height between low tide and high tide.
-
16N.1.SL.TZ0.T_15c:
Find the value of .
-
21M.3.AHL.TZ1.1b:
Find the angle through which Mars rotates on its axis each hour.
-
20N.1.SL.TZ0.T_11a:
Write down the other solution of .
-
20N.1.SL.TZ0.T_2c:
Kaelani has .
Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
-
EXN.1.SL.TZ0.6a.iii:
Find the value of .
-
EXN.1.SL.TZ0.6b:
Find the value of at which the population first reaches .
-
EXN.3.AHL.TZ0.1b:
Assuming the proportion of marked fish in the second sample is equal to the proportion of marked fish in the lake, show that the estate manager will estimate there are now fish in the lake.
-
EXN.3.AHL.TZ0.1g.i:
Assuming a carrying capacity of use the given values of and to calculate the parameters and .
-
21M.1.SL.TZ1.4a:
Find the total cost of buying litres of gas at Leon’s gas station.
-
21M.1.SL.TZ1.4b:
Find .
-
21M.1.AHL.TZ2.2b:
Find an expression for the inverse function. The domain is not required.
-
21M.2.SL.TZ1.2i:
The endpoints of the minute hand and hour hand meet when .
Find the smallest possible value of .
-
21M.2.SL.TZ1.2h:
Write down the amplitude of .
-
21M.2.SL.TZ1.5c.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
-
21N.1.SL.TZ0.5b.ii:
In the context of the question, interpret your answer to part (b)(i).
-
21N.1.SL.TZ0.13a.i:
Write down the value of .
-
21N.1.SL.TZ0.13a.ii:
Hence form two equations in terms of and .
-
21N.1.AHL.TZ0.12b:
Assuming that the model found in part (a) remains valid, estimate the percentage of trees in stock when .
-
21N.1.AHL.TZ0.10b:
On the same set of axes draw the graph of , showing any intercepts and asymptotes.
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
22M.1.SL.TZ1.11b:
Find the value of .
-
22M.1.SL.TZ1.11a:
Find the value of .
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.SL.TZ2.9b.iii:
Hence, or otherwise, find the values of and .
-
22M.1.SL.TZ2.12a:
Determine an equation for the axis of symmetry of the parabola that models the archway.
-
22M.2.SL.TZ1.1b.iii:
the equation of the principal axis.
-
22M.2.SL.TZ1.1d:
For the first year of the model, find the length of time when there are more than hours and minutes of daylight per day.
-
SPM.1.AHL.TZ0.14b:
The outer dome of a large cathedral has the shape of a hemisphere of diameter 32 m, supported by vertical walls of height 17 m. It is also supported by an inner dome which can be modelled by rotating the curve through 360° about the -axis between = 0 and = 33, as indicated in the diagram.
Find the volume of the space between the two domes.
-
SPM.2.SL.TZ0.5e:
Use Model B to calculate an estimate for the braking distance at a speed of .
-
EXM.3.AHL.TZ0.7c.ii:
Find the value of this area.
-
EXM.3.AHL.TZ0.7d.ii:
Hence explain how a straight line graph could be drawn using the coordinates in the table.
-
EXM.3.AHL.TZ0.9g:
Hence predict the total number of people infected by this disease after several months.
-
EXM.3.AHL.TZ0.9h:
Use the logistic model to find the day when the rate of increase of people infected is greatest.
-
22M.2.AHL.TZ2.7d:
Sketch the graph of against , labelling the maximum point of the graph with its coordinates.
-
22M.3.AHL.TZ1.1b.ii:
Using the data in the table write down the equation for an appropriate non-linear regression model.
-
16N.1.SL.TZ0.S_1b:
(i) Write down the value of .
(ii) Find the value of .
-
16N.2.SL.TZ0.T_1e:
Write down the equation of the regression line on for these eight male students.
-
17N.2.SL.TZ0.T_5b.i:
Expand the expression for .
-
18N.1.SL.TZ0.S_8b:
Find the equation of the axis of symmetry of the graph of .
-
18N.1.SL.TZ0.T_11b:
Find the gradient of this tangent at point P.
-
18M.1.SL.TZ2.T_11c:
Calculate the value of x for which f(x) = 0 .
-
18M.1.SL.TZ2.T_14c:
Find the x-coordinate of the point at which the normal to the graph of f has gradient .
-
18M.2.SL.TZ1.T_4c:
Use your answer to part (b) to show that the minimum value of f(x) is −22 .
-
17N.1.SL.TZ0.T_14b:
Find the point on the graph of at which the gradient of the tangent is equal to 6.
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
18N.3.AHL.TZ0.Hsrg_4c:
Find the inverse of .
-
16N.2.SL.TZ0.S_1a:
Find .
-
17M.1.SL.TZ1.T_12c:
Find the range of values of for which has no solution.
-
17M.1.AHL.TZ2.H_2c:
Write down the domain and range of .
-
19M.1.AHL.TZ1.H_8c:
find the value of .
-
19M.1.AHL.TZ1.H_8d:
Sketch the curve , 0 ≤ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.
-
17M.1.AHL.TZ1.H_11e:
Sketch the graph of .
-
17M.1.AHL.TZ1.H_11f:
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
-
17N.2.SL.TZ0.S_10a:
Show that .
-
18M.2.AHL.TZ2.H_10a.iii:
Explain why has no inverse on the given domain.
-
17M.2.AHL.TZ1.H_12e:
Find the inverse function and state its domain.
-
17M.2.AHL.TZ1.H_12f:
Find .
-
17M.2.SL.TZ2.S_6b:
On the following grid, sketch the graph of , for .
-
19N.1.SL.TZ0.T_11b:
Calculate the time taken for the number of Elvis impersonators to reach .
-
19N.2.SL.TZ0.T_4a:
Find the value of .
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
17M.2.SL.TZ1.S_8c:
There are two high tides on 12 December 2017. At what time does the second high tide occur?
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
17M.2.SL.TZ1.S_8b.iii:
Find the value of .
-
21M.3.AHL.TZ1.1d.i:
the maximum value of .
-
20N.2.SL.TZ0.S_8a.ii:
Calculate the number of seconds it takes for the water wheel to complete one rotation.
-
20N.1.SL.TZ0.T_11b:
Complete the table below placing a tick (✔) to show whether the unknown parameters and are positive, zero or negative. The row for has been completed as an example.
-
EXN.1.SL.TZ0.6a.ii:
Find the value of .
-
EXN.1.AHL.TZ0.12c.i:
Use your answer to part (b) to write down the value of to the nearest integer.
-
EXN.1.AHL.TZ0.12b:
Find the equation of the least squares regression line of against .
-
EXN.1.AHL.TZ0.12a:
Explain why this graph indicates that is inversely proportional to .
-
EXN.2.SL.TZ0.3b.i:
Find the value of at which the ball hits the ground.
-
EXN.2.SL.TZ0.3a:
Find an expression for the height of the ball at time .
-
21M.1.AHL.TZ1.17:
The graph of the function is translated by so that it then passes through the points and .
Find the value of and the value of .
-
21M.2.SL.TZ1.5a.i:
Find .
-
21M.2.AHL.TZ1.2a.i:
Find .
-
21M.2.AHL.TZ1.2d.ii:
Hence find the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.4b.ii:
By considering the gradient of this curve when , explain why it may not be a good model.
-
21N.1.SL.TZ0.5b.i:
Find .
-
21N.1.SL.TZ0.5b.iii:
Write down the range of .
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.AHL.TZ0.2b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
22M.1.AHL.TZ1.12c:
Find the average number of earthquakes in a year with a magnitude of at least .
-
22M.1.AHL.TZ1.12a:
Find the value of .
-
22M.1.AHL.TZ1.12b:
Find the value of .
-
22M.1.SL.TZ2.12b:
Determine whether the crate will fit through the archway. Justify your answer.
-
22M.1.AHL.TZ2.10a:
Find an expression for . You are not required to state a domain.
-
22M.2.SL.TZ1.1c:
Hence or otherwise find the equation of this model in the form:
-
22M.2.SL.TZ1.1b.i:
the amplitude.
-
22M.2.SL.TZ1.1b.ii:
the period.
-
SPM.1.AHL.TZ0.18:
The rate, , of a chemical reaction at a fixed temperature is related to the concentration of two compounds, and , by the equation
, where , , .
A scientist measures the three variables three times during the reaction and obtains the following values.
Find , and .
-
SPM.2.SL.TZ0.5c:
Using the values in the table and your answer to part (b), sketch the graph of for 0 ≤ ≤ 10 and −10 ≤ ≤ 60, clearly showing the vertex.
-
SPM.2.SL.TZ0.5a.ii:
Find the values of and .
-
22M.2.SL.TZ2.4e.ii:
Find the new value of the parameter identified in part (e)(i).
-
EXM.2.SL.TZ0.3d.i:
when the height of the object is zero.
-
EXM.1.AHL.TZ0.13b.ii:
the value of when .
-
EXM.2.AHL.TZ0.13a:
Calculate her distance after 8 minutes. Give your answer in km, correct to 3 decimal places.
-
EXM.3.AHL.TZ0.9b.i:
the number of new people infected on day 6.
-
EXM.3.AHL.TZ0.7d.iv:
Hence find the area enclosed by the exponential function, the -axis, the -axis and the line .
-
22M.2.AHL.TZ2.6e:
Determine the two positions where the path of the arrow intersects the path of the ball.
-
17N.1.SL.TZ0.T_6b:
Use this ratio to write down in terms of .
-
17M.1.SL.TZ1.T_15b:
Find the value of and of .
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
19M.2.SL.TZ1.S_9d.iii:
Hence or otherwise, find the obtuse angle formed by the tangent line to at and the tangent line to at .
-
19M.2.SL.TZ1.T_4d:
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
-
18N.1.SL.TZ0.S_8c.ii:
Find the value of .
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
17M.2.SL.TZ2.S_4c:
Use the model to find the depth of the water 10 hours after high tide.
-
19M.1.SL.TZ2.T_13a:
Find the value of .
-
19M.1.SL.TZ2.T_13b:
Find the time, in years, for the population to decrease to 20 turtles.
-
19M.1.SL.TZ2.T_15a:
Find the value of if no vases are sold.
-
18M.1.SL.TZ2.T_13a:
Find the cost of producing 70 shirts.
-
18M.1.SL.TZ2.T_14a:
Find f'(x)
-
18M.2.SL.TZ1.T_4a:
Find the value of k.
-
17M.2.SL.TZ1.T_4c:
Find the value of .
-
17M.1.SL.TZ2.T_15:
Consider the following graphs of quadratic functions.
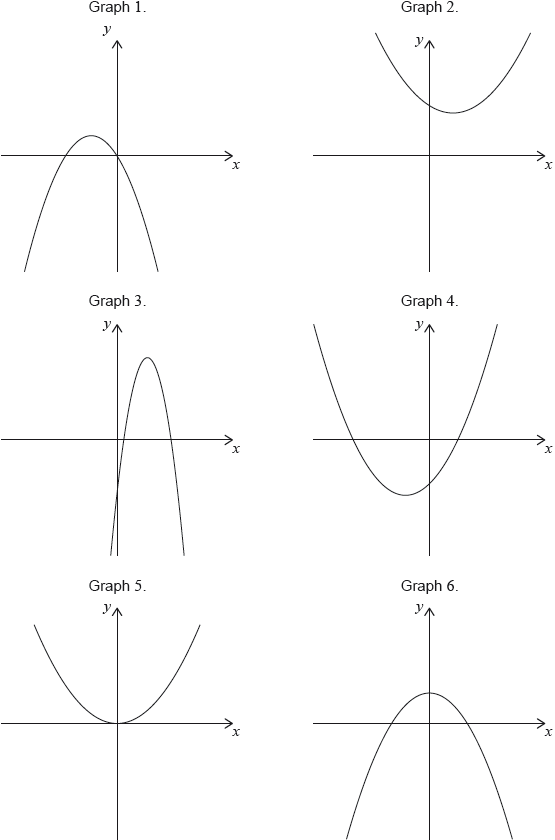
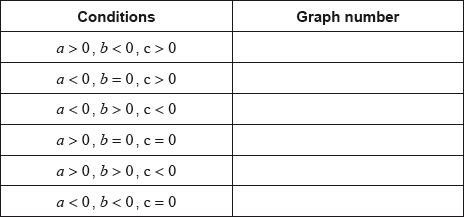
The equation of each of the quadratic functions can be written in the form , where .
Each of the sets of conditions for the constants , and , in the table below, corresponds to one of the graphs above.
Write down the number of the corresponding graph next to each set of conditions.
-
19M.1.AHL.TZ1.H_10b:
Prove that has only one real zero.
-
19M.1.AHL.TZ1.H_10c:
Write down the transformation that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
17N.1.AHL.TZ0.H_6b:
Hence or otherwise, solve the inequality .
-
19M.2.AHL.TZ2.H_4a:
Sketch the graphs and on the following axes for 0 < ≤ 9.
-
16N.2.SL.TZ0.S_1b:
Find .
-
16N.2.SL.TZ0.S_1c:
Solve .
-
18M.1.SL.TZ2.S_5b:
Another function, , can be written in the form . The following diagram shows the graph of .
Write down the value of a and of b.
-
17M.2.SL.TZ2.T_6g:
The equation , where , has four solutions. Find the possible values of .
-
17M.1.AHL.TZ2.H_2a:
Write down the range of .
-
17N.2.AHL.TZ0.H_10b:
Sketch the graph of showing clearly the minimum point and any asymptotic behaviour.
-
17M.2.AHL.TZ1.H_12b:
Sketch the graph of showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
-
17M.1.SL.TZ2.T_13b:
Find the equation of . Give your answer in the form where , , .
-
17M.2.SL.TZ1.T_6b.ii:
Find the equation of the tangent to the graph of at . Give your answer in the form .
-
19N.2.SL.TZ0.T_2d:
Find the value of .
-
17M.2.SL.TZ1.S_8a.i:
How much time is there between the first low tide and the next high tide?
-
17M.2.SL.TZ1.S_8b.i:
Find the value of ;
-
19M.1.AHL.TZ2.H_11d:
Find the coordinates of P.
-
19M.1.AHL.TZ2.H_11c:
Sketch the graphs of and on the same axes, clearly stating the points of intersection with any axes.
-
21M.3.AHL.TZ1.1c.i:
Show that the maximum value of , correct to three significant figures.
-
20N.1.SL.TZ0.S_10b:
Find the area of triangle in terms of .
-
20N.2.SL.TZ0.S_1a:
Find .
-
20N.2.SL.TZ0.S_1c:
The graph of has a local minimum at point .
Find the coordinates of .
-
20N.2.SL.TZ0.S_8d:
Determine the rate of change of when the top of the bucket is at .
-
20N.1.SL.TZ0.T_11c:
State the values of for which is decreasing.
-
20N.1.SL.TZ0.T_4b:
Consider the function .
Solve .
-
EXN.1.AHL.TZ0.12c.ii:
Find an expression for in terms of .
-
EXN.2.AHL.TZ0.4d:
Find the equation for Jorge’s model.
-
EXN.3.AHL.TZ0.1a:
Use this model to predict the number of fish in the lake when .
-
21M.1.SL.TZ1.7a:
Find the value of .
-
21M.1.SL.TZ1.7b:
Use this model to find the percentage of information retained by his students hours after Professor Wei’s lecture.
-
21M.1.SL.TZ1.11b:
Sketch the curve of on the axes below showing clearly the point .
-
21M.1.SL.TZ2.1a.i:
the initial dose of the drug.
-
21M.1.AHL.TZ2.5c:
Comment on the validity of your answer to part (b).
-
21N.1.SL.TZ0.3b:
Find the value of .
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
22M.2.SL.TZ2.2e:
Comment on the appropriateness of modelling this scenario with a geometric sequence.
-
SPM.1.SL.TZ0.5a.i:
Find the population of the Bulbul birds at the start of the migration season.
-
SPM.1.SL.TZ0.5c:
According to this model, find the smallest possible population of Bulbul birds during the migration season.
-
22M.2.SL.TZ2.3g:
State one criticism of this interpretation.
-
SPM.2.SL.TZ0.5d:
Hence, identify why Model A may not be appropriate at lower speeds.
-
22M.2.SL.TZ2.4a.i:
.
-
22M.2.SL.TZ2.4a.iii:
.
-
EXM.1.AHL.TZ0.13a:
Find the equation of the straight line, giving your answer in the form , where .
-
EXM.2.SL.TZ0.3b:
Write down two more equations for , and .
-
EXM.1.AHL.TZ0.15b:
Find the equation of the regression line of on .
-
EXM.2.AHL.TZ0.13c.ii:
her maximum speed, in ms–1.
-
22M.3.AHL.TZ1.1c:
Use your answer from part (b)(ii) to estimate the time taken for the number of infected computers to double.
-
16N.2.SL.TZ0.T_1h:
Write down a reason why this estimate is not reliable.
-
19M.2.SL.TZ1.T_4b.ii:
State the domain of .
-
18N.1.SL.TZ0.S_8c.i:
Write down the value of .
-
18N.1.SL.TZ0.T_15c:
Write down the maximum amount of yeast in this solution.
-
18M.1.SL.TZ1.S_3c:
On the grid above, sketch the graph of f −1.
-
17N.1.SL.TZ0.T_12b:
Find the value of .
-
18M.1.SL.TZ1.T_12c:
Hence find the value of a and of b.
-
18M.1.SL.TZ1.T_9a.ii:
Find the number of fruit flies that are in the container after 6 days.
-
17M.2.SL.TZ1.T_4d:
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
-
18M.2.SL.TZ2.T_6f:
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
-
19M.1.SL.TZ2.S_4b:
Find the -intercept of the graph of .
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
17M.1.SL.TZ2.T_14c:
Calculate how much extra money Jashanti needs.
-
18N.3.AHL.TZ0.Hsrg_4a.i:
Find .
-
18N.3.AHL.TZ0.Hsrg_4a.ii:
Find .
-
18M.1.SL.TZ2.S_5a:
On the same axes, sketch the graph of .
-
16N.2.SL.TZ0.S_6a:
Use the model to find the volume of the barrel.
-
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation .
-
17M.1.SL.TZ1.T_12b.ii:
Write down the number of solutions to .
-
19M.1.AHL.TZ2.H_3:
Consider the function , .
The graph of is translated two units to the left to form the function .
Express in the form where , , , , .
-
17M.1.AHL.TZ1.H_11b:
Sketch the graph of , indicating on it the equations of the asymptotes, the coordinates of the -intercept and the local maximum.
-
18M.2.AHL.TZ2.H_10a.iv:
Explain why is not a function for .
-
17N.2.AHL.TZ0.H_10c:
Find the coordinates of the point on the graph of where the normal to the graph is parallel to the line .
-
17N.2.AHL.TZ0.H_10d:
This region is now rotated through radians about the -axis. Find the volume of revolution.
-
17M.2.AHL.TZ1.H_12c:
Explain why is an even function.
-
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to ;
-
19N.1.SL.TZ0.T_11d:
The world population in is projected to be people.
Use this information to explain why the model for the number of Elvis impersonators is unrealistic.
-
19N.2.SL.TZ0.T_2f:
Given that the length of is , find the area of triangle .
-
19N.2.SL.TZ0.T_4d:
Write down the -intercepts of the graph.
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
18M.2.SL.TZ1.S_10a:
Find the coordinates of A.
-
19M.1.AHL.TZ2.H_11a:
Describe the transformation by which is transformed to .
-
21M.3.AHL.TZ1.1g:
Find the value of .
-
21M.3.AHL.TZ1.1c.ii:
Find the minimum value of .
-
21M.3.AHL.TZ1.1d.ii:
the minimum value of .
-
20N.1.SL.TZ0.S_10a.i:
Find in terms of and .
-
20N.2.SL.TZ0.S_8a.iii:
Hence find the number of rotations the water wheel makes in one hour.
-
20N.1.SL.TZ0.T_12a:
Find the value of .
-
20N.1.SL.TZ0.T_2b:
Write down the minimum number of pizzas that can be ordered.
-
EXN.2.SL.TZ0.3c:
Find the range of .
-
EXN.3.AHL.TZ0.1h:
Comment on the likelihood of the fish population reaching .
-
21M.1.SL.TZ1.7d:
Write down one possible limitation of the domain of the model.
-
21M.1.SL.TZ2.1b:
Calculate the amount of the drug remaining in the body hours after the injection.
-
21M.1.SL.TZ2.7a:
Find the range of .
-
21M.1.AHL.TZ2.5b:
Find the value of .
-
21N.1.SL.TZ0.4b:
Write down the gradient of the line through and .
-
21N.1.SL.TZ0.4c:
Find the equation of the line through and . Give your answer in the form , where and are integers.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.
-
21N.2.AHL.TZ0.2c.ii:
Find the period of the function.
-
22M.1.SL.TZ1.3a:
Write down the height of the ball above the ground at the instant it is hit by the bat.
-
22M.1.SL.TZ1.4a:
Find the equation of the line that the road follows.
-
22M.1.SL.TZ2.9a:
Write down one feature of this graph which suggests a cubic function might be appropriate to model this scenario.
-
22M.1.SL.TZ2.9b.i:
Write down the value of .
-
22M.1.SL.TZ2.9c:
Use the model to determine the total length of time, in years, for which a graduate is expected to be in debt after graduating from university.
-
22M.1.SL.TZ2.11c:
Determine the number of lines parallel to that are tangent to . Justify your answer.
-
22M.1.AHL.TZ2.10b:
Solve .
-
SPM.1.SL.TZ0.5b:
Calculate the time taken for the population to decrease below 1400.
-
SPM.2.SL.TZ0.5f:
Calculate the percentage error in the estimate in part (e).
-
22M.2.SL.TZ2.4c.ii:
an appropriate range for .
-
22M.2.SL.TZ2.4a.ii:
.
-
22M.2.SL.TZ2.4e.i:
Identify which parameter will change.
-
22M.2.SL.TZ2.4d:
By considering the graph of , determine the length of time during one revolution of the Ferris wheel for which the chair is higher than the cowboy statue.
-
EXM.2.AHL.TZ0.13b:
Find the value of , , and .
-
EXM.3.AHL.TZ0.7b.ii:
Write down the coefficient of determination.
-
22M.2.AHL.TZ2.6f:
Determine the time when the arrow should be released to hit the ball before the ball reaches its maximum height.
-
22M.3.AHL.TZ1.1f.ii:
The solution to the differential equation is given by
where is a constant.
Using your answer to part (f)(i), estimate the percentage of computers in city X that are expected to have been infected by the virus over a long period of time.
-
16N.1.SL.TZ0.S_1a:
Find the equation of the axis of symmetry of the graph of .
-
17N.1.SL.TZ0.T_2c.ii:
Write down, in the form , the equation of .
-
16N.2.SL.TZ0.T_1g:
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
-
17N.2.SL.TZ0.T_5d:
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
-
19M.2.SL.TZ1.S_9d.i:
Find .
-
18N.1.SL.TZ0.T_11c:
Find the equation of this tangent. Give your answer in the form y = mx + c.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18M.1.SL.TZ1.T_12b:
Using this information, write down a second equation in terms of a and b.
-
18M.1.SL.TZ1.T_9b:
The maximum capacity of the container is 8000 fruit flies.
Find the number of days until the container reaches its maximum capacity.
-
18M.1.SL.TZ2.S_6:
Let , where p ≠ 0. Find Find the number of roots for the equation .
Justify your answer.
-
18M.1.SL.TZ2.T_10c:
Find the time since the experiment began for the bacteria population to be equal to 40A.
-
17M.2.SL.TZ1.T_4f:
In the context of this model, state what the value of 19 represents.
-
19M.1.SL.TZ2.S_4a.ii:
Find the -intercept of the graph of .
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
17M.2.SL.TZ1.T_3c:
Write down the equation of the vertical asymptote.
-
17M.2.SL.TZ1.T_3e:
Write down the possible values of for which and .
-
19M.2.AHL.TZ2.H_4b:
Hence solve in the range 0 < ≤ 9.
-
18N.3.AHL.TZ0.Hsrg_4b:
State with a reason whether or not and commute.
-
17M.2.SL.TZ2.T_6d.i:
Write down the -coordinates of these two points;
-
17M.1.SL.TZ1.T_12b.i:
Draw the line on the axes.
-
17M.1.AHL.TZ1.H_11c:
Show that .
-
17N.2.SL.TZ0.S_10c:
Show that the distance between the -coordinates of and is .
-
18M.2.AHL.TZ2.H_10c:
Sketch the graph of for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.
-
17N.2.AHL.TZ0.H_10a.i:
Show that the -coordinate of the minimum point on the curve satisfies the equation .
-
17M.1.AHL.TZ1.H_6a:
Sketch the graphs on the same set of axes.
-
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function does not exist.
-
16N.2.AHL.TZ0.H_5b:
State the range of .
-
16N.2.AHL.TZ0.H_5c:
Solve the inequality .
-
17M.2.SL.TZ1.T_6e:
Find the -coordinate of the local minimum.
-
19N.1.SL.TZ0.T_10b:
While in Kota Kinabalu, Criselda spent . She returned to the Currency Exchange counter and changed the remainder of her into .
Calculate the amount of she received.
-
19N.2.SL.TZ0.T_4c:
Use the symmetry of the graph to show that the second solution is .
-
19N.2.SL.TZ0.T_4f.i:
Write down the equation of .
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
18M.2.SL.TZ1.S_10d:
Find the maximum speed of the ball.
-
19M.1.AHL.TZ2.H_11b:
State the range of .
-
19M.1.AHL.TZ2.H_11e:
The tangent to at P passes through the origin (0, 0).
Determine the value of .
-
21M.3.AHL.TZ1.1a:
Show that .
-
21M.3.AHL.TZ1.1e:
Hence show that , correct to two significant figures.
-
20N.2.SL.TZ0.S_1b:
Solve .
-
20N.1.SL.TZ0.T_12b:
In the context of the model, state what the horizontal asymptote represents.
-
20N.1.SL.TZ0.T_2a.ii:
State, in the context of the question, what the value of represents.
-
EXN.1.SL.TZ0.6a.i:
Find the value of .
-
EXN.1.AHL.TZ0.8b:
Write down a sequence of transformations that will transform the graph of onto the graph of .
-
21M.1.SL.TZ1.7c:
State a mathematical reason why Professor Wei might believe this.
-
21M.1.AHL.TZ2.5a:
Estimate the value of Roger’s laptop after years.
-
21M.1.AHL.TZ2.2c:
Write down the range of .
-
21M.2.AHL.TZ1.2c:
Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2d.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
-
21N.1.SL.TZ0.3a:
Write down the value of .
-
21N.1.SL.TZ0.4a:
Find the gradient of the line through and .
-
21N.1.SL.TZ0.4d:
Write down the -coordinate of point .
-
21N.2.AHL.TZ0.2a.i:
maximum value of .
-
21N.2.AHL.TZ0.2b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
22M.1.AHL.TZ1.17:
A function is of the form . Part of the graph of is shown.
The points and have coordinates and , and lie on .
The point is a local maximum and the point is a local minimum.
Find the value of , of and of .
-
SPM.2.SL.TZ0.5b:
Find the coordinates of the vertex of the graph of .
-
22M.1.SL.TZ1.3c:
State an appropriate domain for in this model.
-
22M.2.SL.TZ2.5c.i:
Find the value of .
-
EXM.1.AHL.TZ0.15c.i:
find the value of and of .
-
EXM.2.SL.TZ0.3d.ii:
the maximum height of the object.
-
EXM.1.AHL.TZ0.15a:
Show that .
-
22M.2.SL.TZ2.5d:
Sketch the graph of against , labelling the maximum point and the -intercepts with their coordinates.
-
EXM.1.AHL.TZ0.15c.ii:
predict the temperature of the metal rod after 3 minutes.
-
EXM.3.AHL.TZ0.7a.i:
Use the trapezoidal rule to find an estimate for the area.
-
EXM.3.AHL.TZ0.7a.ii:
With reference to the shape of the graph, explain whether your answer to part (a)(i) will be an over-estimate or an underestimate of the area.
-
EXM.3.AHL.TZ0.9e:
Give two reasons why the prediction in part (b)(ii) might be lower than 14.
-
EXM.3.AHL.TZ0.7b.i:
Use all the coordinates in the table to find the equation of the least squares cubic regression curve.
-
EXM.3.AHL.TZ0.7c.i:
Write down an expression for the area enclosed by the cubic function, the -axis, the -axis and the line .
-
EXM.3.AHL.TZ0.9a:
Use an exponential regression to find the value of and of , correct to 4 decimal places.
-
EXM.3.AHL.TZ0.9f.i:
.
-
22M.2.AHL.TZ2.6c:
Assuming that the ground is horizontal and the ball is not hit by the arrow, find the coordinate of the point where the ball lands.
-
16N.1.AHL.TZ0.H_3a:
state the value of and the value of ;
-
16N.1.AHL.TZ0.H_3b:
find the value of .
-
17N.1.SL.TZ0.T_15d:
Find the price, , that will give Maria the highest weekly profit.
-
19M.2.SL.TZ1.S_9b:
Find u.
-
19M.2.SL.TZ1.S_9d.ii:
Hence, write down .
-
19M.2.SL.TZ1.T_4e:
This straight road crosses the highway and then carries on due north.
State whether the straight road will ever cross the river. Justify your answer.
-
18N.1.SL.TZ0.T_11a:
Find .
-
17M.2.SL.TZ2.S_4b:
Find the value of .
-
16N.2.SL.TZ0.S_10a:
(i) Find the value of .
(ii) Show that .
(iii) Find the value of .
-
19M.1.SL.TZ2.T_13c:
There is a number beyond which the turtle population will not decrease.
Find the value of . Justify your answer.
-
18M.1.SL.TZ1.T_12a:
Using only this information, write down an equation in terms of a and b.
-
18M.1.SL.TZ2.T_10a:
Find the value of A.
-
18M.1.SL.TZ2.T_14b:
Find the gradient of the graph of f at .
-
18M.1.SL.TZ2.T_5a.ii:
Write down the amount of interest he earned after 5 years.
-
18M.1.SL.TZ2.T_6a:
Find the value of a.
-
18M.1.SL.TZ1.S_4a.ii:
Hence, show that a = 2.
-
17M.1.SL.TZ2.T_4b:
Find the equation of in the form .
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6e:
Find .
-
19M.1.AHL.TZ1.H_10a.ii:
Find the remainder when is divided by .
-
17M.2.SL.TZ1.T_3a:
Calculate .
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
18M.1.AHL.TZ1.H_9b.ii:
The coordinates of B can be expressed in the form B where a, b. Find the value of a and the value of b.
-
18M.1.AHL.TZ1.H_9c:
Sketch the graph of showing clearly the position of the points A and B.
-
17M.2.SL.TZ2.T_6a:
Write down the -intercept of the graph.
-
17M.2.SL.TZ2.T_6b:
Find .
-
17M.2.SL.TZ2.T_6e:
Write down the range of .
-
17M.1.SL.TZ1.T_12a:
Write down the domain of the function.
-
17M.1.AHL.TZ1.H_11a.i:
Express in the form .
-
17M.1.AHL.TZ1.H_11d:
Hence find the value of if .
-
18M.2.AHL.TZ2.H_10d.i:
Find and β in terms of .
-
18M.2.AHL.TZ2.H_10d.ii:
Show that + β < −2.
-
16N.2.AHL.TZ0.H_5a:
Sketch the graph of indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
-
17M.1.SL.TZ2.T_13c:
Draw the line on the diagram above.
-
17M.2.SL.TZ1.T_6d.i:
Find .
-
19N.1.SL.TZ0.T_2b:
Find the total amount charged for an order of T-shirts.
-
19N.1.SL.TZ0.T_2c:
Write down the number of T-shirts in an order for which EnYear charged euros.
-
19N.2.SL.TZ0.T_4g:
Given and , state whether the function, , is increasing or decreasing at . Give a reason for your answer.
-
18M.2.SL.TZ2.S_6c:
Find when the seat is 30 m above the ground for the third time.
-
18M.2.SL.TZ1.S_10b.ii:
For the graph of , write down the period.
-
17M.2.SL.TZ2.S_3a:
Write down the range of .
-
16N.1.SL.TZ0.T_15a:
Write down, and simplify, an expression for the car’s value when Gabriella purchased it.
-
21M.2.SL.TZ2.3c:
Determine the first year in which this model predicts the average number of visitors per concert will exceed the total seating capacity of the concert hall.
-
20N.2.SL.TZ0.S_4b.i:
Solve the equation .
-
20N.2.SL.TZ0.S_4b.ii:
Hence or otherwise, given that , find the value of .
-
20N.1.SL.TZ0.T_12c:
Find Jean-Pierre’s vertical speed after seconds. Give your answer in .
-
20N.1.SL.TZ0.T_2a.i:
State, in the context of the question, what the value of represents.
-
20N.1.SL.TZ0.T_4a.i:
Write down the zero of .
-
EXN.2.SL.TZ0.6f:
Hence find an expression for .
-
EXN.3.AHL.TZ0.1g.ii:
Use these parameters to calculate the value of predicted by this model.
-
21M.1.SL.TZ2.12c:
Write down the equation of the axis of symmetry of the graph.
-
21M.1.SL.TZ2.1a.ii:
the percentage of the drug that leaves the body each hour.
-
21M.2.SL.TZ1.2g:
Find the value of when .
-
21M.2.SL.TZ1.5b:
Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2b.i:
.
-
21M.2.AHL.TZ1.2b.ii:
.
-
21M.2.AHL.TZ1.4c:
Find the equation of the new model.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
22M.1.SL.TZ1.4b:
Town is due north of town and the road passes through town .
Find the -coordinate of town .
-
22M.1.SL.TZ2.4a:
Calculate the pH of the coffee.
-
22M.2.SL.TZ1.1a:
Write down one reason why a quadratic function would not be a good model for the number of hours of daylight per day, across a number of years.
-
SPM.1.SL.TZ0.8a:
An orchestra has a sound intensity of 6.4 × 10−3 W m−2 . Calculate the intensity level, of the orchestra.
-
22M.2.SL.TZ2.3c:
Find the coordinates of .
-
SPM.2.SL.TZ0.5a.i:
Write down a second equation to represent Model A, when the speed is .
-
22M.2.AHL.TZ2.7f:
Write down one reason, with reference to the context, to support this decision.
-
22M.2.AHL.TZ2.4d:
Find the equation of the regression line for on .
-
EXM.3.AHL.TZ0.9b.ii:
the day when the total number of people infected will be greater than 1000.
-
EXM.3.AHL.TZ0.9f.iii:
.
-
EXM.3.AHL.TZ0.9d.ii:
Perform a goodness of fit test at the 5% significance level. You should clearly state your hypotheses, the p-value, and your conclusion.
-
EXM.3.AHL.TZ0.9c:
Use your answer to part (a) to show that the model predicts 16.7 people will be infected on the first day.
-
22M.2.AHL.TZ2.7e:
Use the model to calculate the total amount of time when fishing should be stopped.
-
16N.2.SL.TZ0.T_1a:
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the -axis and 2 cm to represent 10 points on the -axis.
-
16N.2.SL.TZ0.T_1b:
(i) , the mean number of hours spent on social media;
(ii) , the mean number of IB Diploma points.
-
16N.2.SL.TZ0.T_1f:
Draw the regression line, from part (e), on your scatter diagram.
-
17N.1.SL.TZ0.T_6a:
Use this information to write down an equation involving and .
-
17M.1.SL.TZ1.T_15c:
Write down the second -intercept of the function.
-
19M.2.SL.TZ1.S_9c:
Find the acute angle between and .
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
17N.1.SL.TZ0.T_12c:
Find the total time that the baking tin is in the oven.
-
16N.2.SL.TZ0.S_10c:
(i) Find .
(ii) Hence or otherwise, find the maximum positive rate of change of .
-
19M.1.SL.TZ2.T_15b:
Differentiate .
-
18M.1.SL.TZ1.T_12d:
The graph intersects the x-axis at a second point, P.
Find the x-coordinate of P.
-
18M.1.SL.TZ2.T_13b:
Find the value of s.
-
18M.1.SL.TZ2.T_5a.i:
Calculate the amount of money he has in the account after 5 years.
-
18M.2.SL.TZ1.T_4b:
Using your value of k , find f ′(x).
-
17M.1.SL.TZ2.T_4c:
Find the -coordinate of point A.
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
17M.1.SL.TZ2.T_4a:
Find the gradient of .
-
19M.1.AHL.TZ1.H_10d:
The random variable follows a Poisson distribution with a mean of and .
Find the value of .
-
17M.2.SL.TZ1.T_3b:
Sketch the graph of for and .
-
17N.1.AHL.TZ0.H_6a:
Sketch the graph of , showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.

-
18M.1.AHL.TZ1.H_9b.i:
Show that there is exactly one point of inflexion, B, on the graph of .
-
18M.1.AHL.TZ2.H_2b:
Solve the equation .
-
17M.2.SL.TZ2.T_6c.ii:
Find .
-
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of is positive.
-
19M.1.AHL.TZ1.H_8a:
Write down the -coordinate of the point of inflexion on the graph of .
-
19M.1.AHL.TZ1.H_8b:
find the value of .
-
17N.1.SL.TZ0.S_5a:
Find .
-
17M.1.AHL.TZ1.H_11a.ii:
Factorize .
-
18M.2.AHL.TZ2.H_10b:
Show that .
-
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain for to be a function.
-
18M.2.SL.TZ2.T_6b:
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.State the name of the student who made an incorrect observation.
-
17M.2.SL.TZ1.T_6d.ii:
Hence justify that is decreasing at .
-
19N.1.SL.TZ0.T_11c:
Calculate the number of Elvis impersonators when .
-
19N.1.SL.TZ0.T_2a:
Write down the initial design fee charged for each order.
-
19N.1.SL.TZ0.T_2d:
An order of T-shirts will be charged the same price by both M-Line and EnYear.
Find the value of .
-
19N.2.SL.TZ0.T_2a:
Find the gradient of .
-
19N.2.SL.TZ0.T_2b:
Find the coordinates of point .
-
19N.2.SL.TZ0.T_2e:
Find the distance between points and .
-
19N.2.SL.TZ0.T_4e:
On graph paper, draw the graph of for and . Use a scale of to represent unit on the -axis and to represent units on the -axis.
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
18M.2.SL.TZ1.S_10e:
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
-
18M.2.SL.TZ1.S_10c:
Hence, write in the form .
-
21M.2.SL.TZ2.5c:
Sketch the graph of , for .
-
21M.3.AHL.TZ1.1f:
Find the value of .
-
20N.1.SL.TZ0.S_10a.ii:
Show that the equation of is .
-
20N.1.SL.TZ0.S_10c:
The graph of is translated by to give the graph of .
In the following diagram:- point lies on the graph of
- points , and lie on the vertical asymptote of
- points and lie on the horizontal asymptote of
- point lies on the -axis such that is parallel to .
Line is the tangent to the graph of at , and passes through and .
Given that triangle and rectangle have equal areas, find the gradient of in terms of .
-
20N.2.SL.TZ0.S_8a.i:
Find the height of point above the ground.
-
20N.2.SL.TZ0.S_8c:
Find .
-
20N.1.SL.TZ0.T_4a.ii:
Write down the coordinates of the local minimum point.
-
EXN.1.SL.TZ0.2b:
Find, to the nearest USD, the cost of disk that has a radius of cm.
-
21M.1.SL.TZ2.12a:
Find the value of .
-
21M.1.SL.TZ2.7b:
Find the value of .
-
21M.1.AHL.TZ2.2a:
Find the range of .
-
21M.2.SL.TZ1.5a.ii:
Hence find the maximum height of the tunnel.
-
21M.2.AHL.TZ1.4a:
Find the equation of the line passing through these two points.
-
21N.1.SL.TZ0.13a.iii:
Hence find the equation of the quadratic curve.
-
21N.1.SL.TZ0.13b:
Find the area of the shaded region in Irina’s design.
-
21N.2.AHL.TZ0.2a.ii:
minimum value of .
-
21N.2.AHL.TZ0.2c.i:
Write down the amplitude of the function.
-
21N.2.AHL.TZ0.2d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.AHL.TZ0.2e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
22M.1.SL.TZ1.5a:
Write down three equations that express the information given above.
-
22M.1.SL.TZ2.4b:
Determine whether the unknown liquid is more or less acidic than the coffee. Justify your answer mathematically.
-
SPM.1.SL.TZ0.8b:
A rock concert has an intensity level of 112 dB. Find the sound intensity, .
-
22M.2.AHL.TZ1.6b:
Find the value of and the value of .
-
SPM.1.SL.TZ0.5a.ii:
Find the population of the Bulbul birds after 5 days.
-
SPM.1.AHL.TZ0.14a.i:
Write down the value of .
-
22M.2.SL.TZ2.4c.i:
an appropriate domain for .
-
EXM.2.AHL.TZ0.13c.i:
the distance she runs in 20 minutes.
-
EXM.1.AHL.TZ0.13b.i:
a formula for in terms of .
-
EXM.1.AHL.TZ0.14:
It is believed that two variables, and are related by the equation , where . Experimental values of and are obtained. A graph of against shows a straight line passing through (−1.7, 4.3) and (7.1, 17.5).
Find the value of and of .
-
22M.2.AHL.TZ2.4c:
(i) the gradient of this line in terms of ;
(ii) the -intercept of this line in terms of .
-
EXM.3.AHL.TZ0.9d.i:
Explain why the number of degrees of freedom is 2.
-
17N.1.SL.TZ0.T_15a:
Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.
-
17N.2.SL.TZ0.T_5a:
Find the exact value of each of the zeros of .
-
17N.2.SL.TZ0.T_5b.ii:
Find .
-
17M.1.SL.TZ1.T_15a:
Write down the value of .
-
19M.2.SL.TZ2.T_5e:
Find the gradient of the graph of at .
-
19M.2.SL.TZ2.T_5f:
Find the equation of the tangent line to the graph of at . Give the equation in the form where, , , and .
-
16N.2.SL.TZ0.S_10b:
(i) Write down the value of .
(ii) Find .
-
18M.1.SL.TZ2.T_11a:
Write down the equation of the vertical asymptote.
-
18M.1.SL.TZ2.T_11b:
Write down the equation of the horizontal asymptote.
-
18M.1.SL.TZ2.T_13c:
Find the number of shirts produced when the cost of production is lowest.
-
18M.1.SL.TZ2.T_5b:
Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.
Calculate the value of t.
-
18M.1.SL.TZ2.T_6b:
Find the coordinates of R.
-
18M.1.SL.TZ2.T_6c:
Line L3 is parallel to line L2 and passes through the point (2, 3).
Find the equation of line L3. Give your answer in the form y = mx + c.
-
17M.2.SL.TZ1.T_4b:
Find the radius of the sphere in cm, correct to one decimal place.
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
18M.1.AHL.TZ1.H_9a:
The graph of has a local maximum at A. Find the coordinates of A.
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
18M.1.AHL.TZ2.H_10c:
The function is defined by , for ≥ 0.
State the domain and range of .
-
18M.1.AHL.TZ2.H_2a:
Sketch the graphs of and on the following axes.
-
16N.2.SL.TZ0.S_6b:
The empty barrel is being filled with water. The volume of water in the barrel after minutes is given by . How long will it take for the barrel to be half-full?
-
17M.2.SL.TZ2.T_6c.i:
Show that .
-
17M.1.AHL.TZ2.H_2b:
Find an expression for .
-
17N.1.SL.TZ0.S_5b:
Given that , find the value of .
-
17N.2.SL.TZ0.S_10b.i:
Find the coordinates of and of .
-
17N.2.SL.TZ0.S_10b.ii:
Find the equation of .
-
17N.2.SL.TZ0.S_10d:
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
-
17N.2.AHL.TZ0.H_10a.ii:
Determine the values of for which is a decreasing function.
-
17M.1.AHL.TZ1.H_6b:
Given that the graphs enclose a region of area 18 square units, find the value of b.
-
17M.1.SL.TZ2.T_13a:
Write down the value of .
-
19N.1.SL.TZ0.T_10a:
Calculate the amount of that Criselda received.
-
19N.1.SL.TZ0.T_11a:
Write down the number of Elvis impersonators in .
-
19N.2.SL.TZ0.T_4f.ii:
Draw the tangent on your graph.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
18M.2.SL.TZ1.S_10b.i:
For the graph of , write down the amplitude.
-
16N.1.SL.TZ0.T_15b:
Find the value of .
Sub sections and their related questions
SL 2.1—Equations of straight lines, parallel and perpendicular
-
18M.1.SL.TZ2.T_5a.i:
Calculate the amount of money he has in the account after 5 years.
-
18M.1.SL.TZ2.T_5a.ii:
Write down the amount of interest he earned after 5 years.
-
18M.1.SL.TZ2.T_5b:
Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.
Calculate the value of t.
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
17N.1.SL.TZ0.T_2c.ii:
Write down, in the form , the equation of .
-
17M.1.SL.TZ2.T_4a:
Find the gradient of .
-
17M.1.SL.TZ2.T_4b:
Find the equation of in the form .
-
17M.1.SL.TZ2.T_4c:
Find the -coordinate of point A.
-
19N.2.SL.TZ0.T_2a:
Find the gradient of .
-
19N.2.SL.TZ0.T_2b:
Find the coordinates of point .
-
19N.2.SL.TZ0.T_2c:
Find the equation of . Give your answer in the form , where .
-
19N.2.SL.TZ0.T_2d:
Find the value of .
-
19N.2.SL.TZ0.T_2e:
Find the distance between points and .
-
19N.2.SL.TZ0.T_2f:
Given that the length of is , find the area of triangle .
-
21M.2.AHL.TZ1.4a:
Find the equation of the line passing through these two points.
-
21N.1.SL.TZ0.4a:
Find the gradient of the line through and .
-
21N.1.SL.TZ0.4b:
Write down the gradient of the line through and .
-
21N.1.SL.TZ0.4c:
Find the equation of the line through and . Give your answer in the form , where and are integers.
-
21N.1.SL.TZ0.4d:
Write down the -coordinate of point .
-
22M.1.SL.TZ1.4a:
Find the equation of the line that the road follows.
-
22M.1.SL.TZ1.4b:
Town is due north of town and the road passes through town .
Find the -coordinate of town .
-
22M.1.SL.TZ2.11c:
Determine the number of lines parallel to that are tangent to . Justify your answer.
-
22M.2.AHL.TZ2.4c:
(i) the gradient of this line in terms of ;
(ii) the -intercept of this line in terms of .
-
22M.2.AHL.TZ2.4d:
Find the equation of the regression line for on .
SL 2.2—Functions, notation domain, range and inverse as reflection
-
18M.1.AHL.TZ1.H_9a:
The graph of has a local maximum at A. Find the coordinates of A.
-
18M.1.AHL.TZ1.H_9b.i:
Show that there is exactly one point of inflexion, B, on the graph of .
-
18M.1.AHL.TZ1.H_9b.ii:
The coordinates of B can be expressed in the form B where a, b. Find the value of a and the value of b.
-
18M.1.AHL.TZ1.H_9c:
Sketch the graph of showing clearly the position of the points A and B.
-
19M.1.AHL.TZ1.H_8a:
Write down the -coordinate of the point of inflexion on the graph of .
-
19M.1.AHL.TZ1.H_8b:
find the value of .
-
19M.1.AHL.TZ1.H_8c:
find the value of .
-
19M.1.AHL.TZ1.H_8d:
Sketch the curve , 0 ≤ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.
-
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain for to be a function.
-
17M.2.AHL.TZ1.H_12b:
Sketch the graph of showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
-
17M.2.AHL.TZ1.H_12c:
Explain why is an even function.
-
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function does not exist.
-
17M.2.AHL.TZ1.H_12e:
Find the inverse function and state its domain.
-
17M.2.AHL.TZ1.H_12f:
Find .
-
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to ;
-
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to .
-
18M.1.AHL.TZ2.H_10a:
Find the inverse function , stating its domain.
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
18M.1.AHL.TZ2.H_10b.ii:
Sketch the graph of . State the equations of any asymptotes and the coordinates of any intercepts with the axes.
-
18M.1.AHL.TZ2.H_10c:
The function is defined by , for ≥ 0.
State the domain and range of .
-
18M.2.AHL.TZ2.H_10a.i:
Sketch the graph of for .
-
18M.2.AHL.TZ2.H_10a.ii:
With reference to your graph, explain why is a function on the given domain.
-
18M.2.AHL.TZ2.H_10a.iii:
Explain why has no inverse on the given domain.
-
18M.2.AHL.TZ2.H_10a.iv:
Explain why is not a function for .
-
18M.2.AHL.TZ2.H_10b:
Show that .
-
18M.2.AHL.TZ2.H_10c:
Sketch the graph of for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.
-
18M.2.AHL.TZ2.H_10d.i:
Find and β in terms of .
-
18M.2.AHL.TZ2.H_10d.ii:
Show that + β < −2.
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
17M.1.AHL.TZ2.H_2a:
Write down the range of .
-
17M.1.AHL.TZ2.H_2b:
Find an expression for .
-
17M.1.AHL.TZ2.H_2c:
Write down the domain and range of .
-
17N.1.AHL.TZ0.H_6a:
Sketch the graph of , showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.

-
17N.1.AHL.TZ0.H_6b:
Hence or otherwise, solve the inequality .
-
17N.2.AHL.TZ0.H_10a.i:
Show that the -coordinate of the minimum point on the curve satisfies the equation .
-
17N.2.AHL.TZ0.H_10a.ii:
Determine the values of for which is a decreasing function.
-
17N.2.AHL.TZ0.H_10b:
Sketch the graph of showing clearly the minimum point and any asymptotic behaviour.
-
17N.2.AHL.TZ0.H_10c:
Find the coordinates of the point on the graph of where the normal to the graph is parallel to the line .
-
17N.2.AHL.TZ0.H_10d:
This region is now rotated through radians about the -axis. Find the volume of revolution.
-
17M.1.AHL.TZ1.H_11a.i:
Express in the form .
-
17M.1.AHL.TZ1.H_11a.ii:
Factorize .
-
17M.1.AHL.TZ1.H_11b:
Sketch the graph of , indicating on it the equations of the asymptotes, the coordinates of the -intercept and the local maximum.
-
17M.1.AHL.TZ1.H_11c:
Show that .
-
17M.1.AHL.TZ1.H_11d:
Hence find the value of if .
-
17M.1.AHL.TZ1.H_11e:
Sketch the graph of .
-
17M.1.AHL.TZ1.H_11f:
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
-
17M.1.AHL.TZ1.H_6a:
Sketch the graphs on the same set of axes.
-
17M.1.AHL.TZ1.H_6b:
Given that the graphs enclose a region of area 18 square units, find the value of b.
-
19M.2.AHL.TZ2.H_4a:
Sketch the graphs and on the following axes for 0 < ≤ 9.
-
19M.2.AHL.TZ2.H_4b:
Hence solve in the range 0 < ≤ 9.
-
18M.1.AHL.TZ2.H_2a:
Sketch the graphs of and on the following axes.
-
18M.1.AHL.TZ2.H_2b:
Solve the equation .
-
16N.1.AHL.TZ0.H_3a:
state the value of and the value of ;
-
16N.1.AHL.TZ0.H_3b:
find the value of .
-
16N.2.AHL.TZ0.H_5a:
Sketch the graph of indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
-
16N.2.AHL.TZ0.H_5b:
State the range of .
-
16N.2.AHL.TZ0.H_5c:
Solve the inequality .
-
17N.1.SL.TZ0.S_5a:
Find .
-
17N.1.SL.TZ0.S_5b:
Given that , find the value of .
-
18M.1.SL.TZ1.S_3c:
On the grid above, sketch the graph of f −1.
-
17M.2.SL.TZ2.S_6a:
Show that .
-
17M.2.SL.TZ2.S_6b:
On the following grid, sketch the graph of , for .

-
17M.2.SL.TZ2.S_6c:
The equation has exactly two solutions, for . Find the possible values of .
-
17M.2.SL.TZ2.S_3a:
Write down the range of .
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
19M.2.SL.TZ1.S_9b:
Find u.
-
19M.2.SL.TZ1.S_9c:
Find the acute angle between and .
-
19M.2.SL.TZ1.S_9d.i:
Find .
-
19M.2.SL.TZ1.S_9d.ii:
Hence, write down .
-
19M.2.SL.TZ1.S_9d.iii:
Hence or otherwise, find the obtuse angle formed by the tangent line to at and the tangent line to at .
-
16N.2.SL.TZ0.S_1a:
Find .
-
16N.2.SL.TZ0.S_1b:
Find .
-
16N.2.SL.TZ0.S_1c:
Solve .
-
18M.2.SL.TZ1.T_4a:
Find the value of k.
-
18M.2.SL.TZ1.T_4b:
Using your value of k , find f ′(x).
-
18M.2.SL.TZ1.T_4c:
Use your answer to part (b) to show that the minimum value of f(x) is −22 .
-
18M.2.SL.TZ1.T_4e:
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph. -
18M.2.SL.TZ2.T_6a:
Sketch the curve for −1 < x < 3 and −2 < y < 12.
-
18M.2.SL.TZ2.T_6b:
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.State the name of the student who made an incorrect observation.
-
18M.2.SL.TZ2.T_6d:
Find .
-
18M.2.SL.TZ2.T_6f:
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
17M.1.SL.TZ2.T_14b:
Use your graphic display calculator to find how long it will take for Jashanti to have saved enough money to buy the car.
-
17M.1.SL.TZ2.T_14c:
Calculate how much extra money Jashanti needs.
-
17M.1.SL.TZ1.T_12a:
Write down the domain of the function.
-
17M.1.SL.TZ1.T_12b.i:
Draw the line on the axes.
-
17M.1.SL.TZ1.T_12b.ii:
Write down the number of solutions to .
-
17M.1.SL.TZ1.T_12c:
Find the range of values of for which has no solution.
-
19M.2.SL.TZ1.T_4b.ii:
State the domain of .
-
19M.2.SL.TZ1.T_4d:
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
-
19M.2.SL.TZ1.T_4e:
This straight road crosses the highway and then carries on due north.
State whether the straight road will ever cross the river. Justify your answer.
-
19M.2.SL.TZ2.T_5d:
Find .
-
19M.2.SL.TZ2.T_5e:
Find the gradient of the graph of at .
-
19M.2.SL.TZ2.T_5f:
Find the equation of the tangent line to the graph of at . Give the equation in the form where, , , and .
-
16N.1.SL.TZ0.T_9b:
Find the value of .
-
19N.1.SL.TZ0.T_10a:
Calculate the amount of that Criselda received.
-
19N.1.SL.TZ0.T_10b:
While in Kota Kinabalu, Criselda spent . She returned to the Currency Exchange counter and changed the remainder of her into .
Calculate the amount of she received.
-
20N.1.SL.TZ0.T_2a.i:
State, in the context of the question, what the value of represents.
-
20N.1.SL.TZ0.T_2a.ii:
State, in the context of the question, what the value of represents.
-
20N.1.SL.TZ0.T_2b:
Write down the minimum number of pizzas that can be ordered.
-
20N.1.SL.TZ0.T_2c:
Kaelani has .
Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
-
EXN.2.SL.TZ0.3a:
Find an expression for the height of the ball at time .
-
EXN.2.SL.TZ0.3b.i:
Find the value of at which the ball hits the ground.
-
EXN.2.SL.TZ0.3b.ii:
Hence write down the domain of .
-
EXN.2.SL.TZ0.3c:
Find the range of .
-
21M.1.SL.TZ1.4a:
Find the total cost of buying litres of gas at Leon’s gas station.
-
21M.1.SL.TZ1.4b:
Find .
-
21M.1.SL.TZ2.7a:
Find the range of .
-
21M.1.SL.TZ2.7b:
Find the value of .
-
21M.1.AHL.TZ2.2a:
Find the range of .
-
21M.1.AHL.TZ2.2b:
Find an expression for the inverse function. The domain is not required.
-
21M.1.AHL.TZ2.2c:
Write down the range of .
-
21N.1.SL.TZ0.5a:
Find the range of .
-
21N.1.SL.TZ0.5b.i:
Find .
-
21N.1.SL.TZ0.5b.ii:
In the context of the question, interpret your answer to part (b)(i).
-
21N.1.SL.TZ0.5b.iii:
Write down the range of .
-
22M.1.SL.TZ1.3c:
State an appropriate domain for in this model.
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.AHL.TZ2.10b:
Solve .
-
22M.2.SL.TZ2.4c.i:
an appropriate domain for .
-
22M.2.SL.TZ2.4c.ii:
an appropriate range for .
SL 2.3—Graphing
-
SPM.1.SL.TZ0.8a:
An orchestra has a sound intensity of 6.4 × 10−3 W m−2 . Calculate the intensity level, of the orchestra.
-
SPM.1.SL.TZ0.8b:
A rock concert has an intensity level of 112 dB. Find the sound intensity, .
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
18M.2.SL.TZ1.T_4a:
Find the value of k.
-
18M.2.SL.TZ1.T_4b:
Using your value of k , find f ′(x).
-
18M.2.SL.TZ1.T_4c:
Use your answer to part (b) to show that the minimum value of f(x) is −22 .
-
18M.2.SL.TZ1.T_4e:
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph. -
18M.2.SL.TZ2.T_6a:
Sketch the curve for −1 < x < 3 and −2 < y < 12.
-
18M.2.SL.TZ2.T_6b:
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.State the name of the student who made an incorrect observation.
-
18M.2.SL.TZ2.T_6d:
Find .
-
18M.2.SL.TZ2.T_6f:
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
-
17M.1.SL.TZ1.T_12a:
Write down the domain of the function.
-
17M.1.SL.TZ1.T_12b.i:
Draw the line on the axes.
-
17M.1.SL.TZ1.T_12b.ii:
Write down the number of solutions to .
-
17M.1.SL.TZ1.T_12c:
Find the range of values of for which has no solution.
-
19M.2.SL.TZ2.T_5d:
Find .
-
19M.2.SL.TZ2.T_5e:
Find the gradient of the graph of at .
-
19M.2.SL.TZ2.T_5f:
Find the equation of the tangent line to the graph of at . Give the equation in the form where, , , and .
-
17N.2.SL.TZ0.T_5a:
Find the exact value of each of the zeros of .
-
17N.2.SL.TZ0.T_5b.i:
Expand the expression for .
-
17N.2.SL.TZ0.T_5b.ii:
Find .
-
17N.2.SL.TZ0.T_5c:
Use your answer to part (b)(ii) to find the values of for which is increasing.
-
17N.2.SL.TZ0.T_5d:
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
-
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
-
17M.1.SL.TZ2.T_13a:
Write down the value of .
-
17M.1.SL.TZ2.T_13b:
Find the equation of . Give your answer in the form where , , .
-
17M.1.SL.TZ2.T_13c:
Draw the line on the diagram above.
-
19N.2.SL.TZ0.T_4a:
Find the value of .
-
19N.2.SL.TZ0.T_4b:
Write down the equation for the axis of symmetry of the graph.
-
19N.2.SL.TZ0.T_4c:
Use the symmetry of the graph to show that the second solution is .
-
19N.2.SL.TZ0.T_4d:
Write down the -intercepts of the graph.
-
19N.2.SL.TZ0.T_4e:
On graph paper, draw the graph of for and . Use a scale of to represent unit on the -axis and to represent units on the -axis.
-
19N.2.SL.TZ0.T_4f.i:
Write down the equation of .
-
19N.2.SL.TZ0.T_4f.ii:
Draw the tangent on your graph.
-
19N.2.SL.TZ0.T_4g:
Given and , state whether the function, , is increasing or decreasing at . Give a reason for your answer.
-
21M.2.SL.TZ2.5c:
Sketch the graph of , for .
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.AHL.TZ0.2a.i:
maximum value of .
-
21N.2.AHL.TZ0.2a.ii:
minimum value of .
-
21N.2.AHL.TZ0.2b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.AHL.TZ0.2b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.AHL.TZ0.2c.i:
Write down the amplitude of the function.
-
21N.2.AHL.TZ0.2c.ii:
Find the period of the function.
-
21N.2.AHL.TZ0.2d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.AHL.TZ0.2e.i:
Find the height of above the ground when .
-
21N.2.AHL.TZ0.2e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.AHL.TZ0.2f:
The wind speed increases and the blades rotate faster, but still at a constant rate.
Given that point is now higher than for second during each complete rotation, find the time for one complete rotation.
-
22M.2.SL.TZ2.5d:
Sketch the graph of against , labelling the maximum point and the -intercepts with their coordinates.
-
22M.2.AHL.TZ2.4b:
Given that and , sketch the graph of against .
-
22M.2.AHL.TZ2.7d:
Sketch the graph of against , labelling the maximum point of the graph with its coordinates.
SL 2.4—Key features of graphs, intersections using technology
-
18M.1.AHL.TZ1.H_9a:
The graph of has a local maximum at A. Find the coordinates of A.
-
18M.1.AHL.TZ1.H_9b.i:
Show that there is exactly one point of inflexion, B, on the graph of .
-
18M.1.AHL.TZ1.H_9b.ii:
The coordinates of B can be expressed in the form B where a, b. Find the value of a and the value of b.
-
18M.1.AHL.TZ1.H_9c:
Sketch the graph of showing clearly the position of the points A and B.
-
19M.1.AHL.TZ1.H_8a:
Write down the -coordinate of the point of inflexion on the graph of .
-
19M.1.AHL.TZ1.H_8b:
find the value of .
-
19M.1.AHL.TZ1.H_8c:
find the value of .
-
19M.1.AHL.TZ1.H_8d:
Sketch the curve , 0 ≤ ≤ 5 indicating clearly the coordinates of the maximum and minimum points and any intercepts with the coordinate axes.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
17M.2.AHL.TZ1.H_12a:
Find the largest possible domain for to be a function.
-
17M.2.AHL.TZ1.H_12b:
Sketch the graph of showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
-
17M.2.AHL.TZ1.H_12c:
Explain why is an even function.
-
17M.2.AHL.TZ1.H_12d:
Explain why the inverse function does not exist.
-
17M.2.AHL.TZ1.H_12e:
Find the inverse function and state its domain.
-
17M.2.AHL.TZ1.H_12f:
Find .
-
17M.2.AHL.TZ1.H_12g.i:
Hence, show that there are no solutions to ;
-
17M.2.AHL.TZ1.H_12g.ii:
Hence, show that there are no solutions to .
-
18M.1.AHL.TZ2.H_10a:
Find the inverse function , stating its domain.
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
18M.1.AHL.TZ2.H_10b.ii:
Sketch the graph of . State the equations of any asymptotes and the coordinates of any intercepts with the axes.
-
18M.1.AHL.TZ2.H_10c:
The function is defined by , for ≥ 0.
State the domain and range of .
-
18M.2.AHL.TZ2.H_10a.i:
Sketch the graph of for .
-
18M.2.AHL.TZ2.H_10a.ii:
With reference to your graph, explain why is a function on the given domain.
-
18M.2.AHL.TZ2.H_10a.iii:
Explain why has no inverse on the given domain.
-
18M.2.AHL.TZ2.H_10a.iv:
Explain why is not a function for .
-
18M.2.AHL.TZ2.H_10b:
Show that .
-
18M.2.AHL.TZ2.H_10c:
Sketch the graph of for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.
-
18M.2.AHL.TZ2.H_10d.i:
Find and β in terms of .
-
18M.2.AHL.TZ2.H_10d.ii:
Show that + β < −2.
-
17N.1.AHL.TZ0.H_6a:
Sketch the graph of , showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.

-
17N.1.AHL.TZ0.H_6b:
Hence or otherwise, solve the inequality .
-
17N.2.AHL.TZ0.H_10a.i:
Show that the -coordinate of the minimum point on the curve satisfies the equation .
-
17N.2.AHL.TZ0.H_10a.ii:
Determine the values of for which is a decreasing function.
-
17N.2.AHL.TZ0.H_10b:
Sketch the graph of showing clearly the minimum point and any asymptotic behaviour.
-
17N.2.AHL.TZ0.H_10c:
Find the coordinates of the point on the graph of where the normal to the graph is parallel to the line .
-
17N.2.AHL.TZ0.H_10d:
This region is now rotated through radians about the -axis. Find the volume of revolution.
-
17M.1.AHL.TZ1.H_11a.i:
Express in the form .
-
17M.1.AHL.TZ1.H_11a.ii:
Factorize .
-
17M.1.AHL.TZ1.H_11b:
Sketch the graph of , indicating on it the equations of the asymptotes, the coordinates of the -intercept and the local maximum.
-
17M.1.AHL.TZ1.H_11c:
Show that .
-
17M.1.AHL.TZ1.H_11d:
Hence find the value of if .
-
17M.1.AHL.TZ1.H_11e:
Sketch the graph of .
-
17M.1.AHL.TZ1.H_11f:
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
-
17M.1.AHL.TZ1.H_6a:
Sketch the graphs on the same set of axes.
-
17M.1.AHL.TZ1.H_6b:
Given that the graphs enclose a region of area 18 square units, find the value of b.
-
19M.2.AHL.TZ2.H_4a:
Sketch the graphs and on the following axes for 0 < ≤ 9.
-
19M.2.AHL.TZ2.H_4b:
Hence solve in the range 0 < ≤ 9.
-
18M.1.AHL.TZ2.H_2a:
Sketch the graphs of and on the following axes.
-
18M.1.AHL.TZ2.H_2b:
Solve the equation .
-
16N.1.AHL.TZ0.H_3a:
state the value of and the value of ;
-
16N.1.AHL.TZ0.H_3b:
find the value of .
-
16N.2.AHL.TZ0.H_5a:
Sketch the graph of indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
-
16N.2.AHL.TZ0.H_5b:
State the range of .
-
16N.2.AHL.TZ0.H_5c:
Solve the inequality .
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
17M.1.SL.TZ2.T_14b:
Use your graphic display calculator to find how long it will take for Jashanti to have saved enough money to buy the car.
-
17M.1.SL.TZ2.T_14c:
Calculate how much extra money Jashanti needs.
-
19M.2.SL.TZ1.T_4b.ii:
State the domain of .
-
19M.2.SL.TZ1.T_4d:
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
-
19M.2.SL.TZ1.T_4e:
This straight road crosses the highway and then carries on due north.
State whether the straight road will ever cross the river. Justify your answer.
-
17M.1.SL.TZ1.T_15a:
Write down the value of .
-
17M.1.SL.TZ1.T_15b:
Find the value of and of .
-
17M.1.SL.TZ1.T_15c:
Write down the second -intercept of the function.
-
17M.2.SL.TZ2.T_6a:
Write down the -intercept of the graph.
-
17M.2.SL.TZ2.T_6b:
Find .
-
17M.2.SL.TZ2.T_6c.i:
Show that .
-
17M.2.SL.TZ2.T_6c.ii:
Find .
-
17M.2.SL.TZ2.T_6d.i:
Write down the -coordinates of these two points;
-
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of is positive.
-
17M.2.SL.TZ2.T_6e:
Write down the range of .
-
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation .
-
17M.2.SL.TZ2.T_6g:
The equation , where , has four solutions. Find the possible values of .
-
20N.2.SL.TZ0.S_1a:
Find .
-
20N.2.SL.TZ0.S_1b:
Solve .
-
20N.2.SL.TZ0.S_1c:
The graph of has a local minimum at point .
Find the coordinates of .
-
20N.1.SL.TZ0.T_2a.i:
State, in the context of the question, what the value of represents.
-
20N.1.SL.TZ0.T_2a.ii:
State, in the context of the question, what the value of represents.
-
20N.1.SL.TZ0.T_2b:
Write down the minimum number of pizzas that can be ordered.
-
20N.1.SL.TZ0.T_2c:
Kaelani has .
Find the maximum number of large cheese pizzas that Kaelani can order from Olava’s Pizza Company.
-
20N.1.SL.TZ0.T_4a.i:
Write down the zero of .
-
20N.1.SL.TZ0.T_4a.ii:
Write down the coordinates of the local minimum point.
-
20N.1.SL.TZ0.T_4b:
Consider the function .
Solve .
-
21M.1.SL.TZ1.4c:
The price of gas at Erica’s gas station is per litre. A customer must buy a minimum of litres of gas. The total cost at Erica’s gas station is cheaper than Leon’s gas station when .
Find the minimum value of .
-
21M.1.SL.TZ1.8b:
On day of the fitness programmes Daniella runs more than Charlie for the first time.
Find the value of .
-
21M.1.SL.TZ1.11c:
Whilst swimming, Scarlett can hear the siren only if the sound intensity at her location is greater than .
Find the values of where Scarlett cannot hear the siren.
-
21M.2.SL.TZ1.2i:
The endpoints of the minute hand and hour hand meet when .
Find the smallest possible value of .
-
21M.1.AHL.TZ2.5a:
Estimate the value of Roger’s laptop after years.
-
21M.1.AHL.TZ2.5b:
Find the value of .
-
21M.1.AHL.TZ2.5c:
Comment on the validity of your answer to part (b).
-
21M.2.SL.TZ2.3c:
Determine the first year in which this model predicts the average number of visitors per concert will exceed the total seating capacity of the concert hall.
-
21N.1.AHL.TZ0.10a:
Find .
-
21N.1.AHL.TZ0.10b:
On the same set of axes draw the graph of , showing any intercepts and asymptotes.
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.AHL.TZ0.2a.i:
maximum value of .
-
21N.2.AHL.TZ0.2a.ii:
minimum value of .
-
21N.2.AHL.TZ0.2b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.AHL.TZ0.2b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.AHL.TZ0.2c.i:
Write down the amplitude of the function.
-
21N.2.AHL.TZ0.2c.ii:
Find the period of the function.
-
21N.2.AHL.TZ0.2d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.AHL.TZ0.2e.i:
Find the height of above the ground when .
-
21N.2.AHL.TZ0.2e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.AHL.TZ0.2f:
The wind speed increases and the blades rotate faster, but still at a constant rate.
Given that point is now higher than for second during each complete rotation, find the time for one complete rotation.
-
22M.1.SL.TZ2.9a:
Write down one feature of this graph which suggests a cubic function might be appropriate to model this scenario.
-
22M.1.SL.TZ2.12a:
Determine an equation for the axis of symmetry of the parabola that models the archway.
-
22M.1.SL.TZ2.12b:
Determine whether the crate will fit through the archway. Justify your answer.
-
22M.1.AHL.TZ2.10b:
Solve .
-
22M.2.SL.TZ1.1d:
For the first year of the model, find the length of time when there are more than hours and minutes of daylight per day.
-
22M.2.SL.TZ2.3c:
Find the coordinates of .
-
22M.2.SL.TZ2.4d:
By considering the graph of , determine the length of time during one revolution of the Ferris wheel for which the chair is higher than the cowboy statue.
-
22M.2.SL.TZ2.5d:
Sketch the graph of against , labelling the maximum point and the -intercepts with their coordinates.
-
22M.2.SL.TZ2.5e:
Determine the maximum amount of coffee the cafe can make that will not result in a loss of money for the morning.
-
22M.2.AHL.TZ2.6e:
Determine the two positions where the path of the arrow intersects the path of the ball.
-
22M.2.AHL.TZ2.6f:
Determine the time when the arrow should be released to hit the ball before the ball reaches its maximum height.
-
22M.2.AHL.TZ2.7e:
Use the model to calculate the total amount of time when fishing should be stopped.
SL 2.5—Modelling functions
-
SPM.1.SL.TZ0.5a.i:
Find the population of the Bulbul birds at the start of the migration season.
-
SPM.1.SL.TZ0.5a.ii:
Find the population of the Bulbul birds after 5 days.
-
SPM.1.SL.TZ0.5b:
Calculate the time taken for the population to decrease below 1400.
-
SPM.1.SL.TZ0.5c:
According to this model, find the smallest possible population of Bulbul birds during the migration season.
-
SPM.2.SL.TZ0.5a.i:
Write down a second equation to represent Model A, when the speed is .
-
SPM.2.SL.TZ0.5a.ii:
Find the values of and .
-
SPM.2.SL.TZ0.5b:
Find the coordinates of the vertex of the graph of .
-
SPM.2.SL.TZ0.5c:
Using the values in the table and your answer to part (b), sketch the graph of for 0 ≤ ≤ 10 and −10 ≤ ≤ 60, clearly showing the vertex.
-
SPM.2.SL.TZ0.5d:
Hence, identify why Model A may not be appropriate at lower speeds.
-
SPM.2.SL.TZ0.5e:
Use Model B to calculate an estimate for the braking distance at a speed of .
-
SPM.2.SL.TZ0.5f:
Calculate the percentage error in the estimate in part (e).
-
SPM.2.SL.TZ0.5g:
It is found that once a driver realizes the need to stop their vehicle, 1.6 seconds will elapse, on average, before the brakes are engaged. During this reaction time, the vehicle will continue to travel at its original speed.
A truck approaches an intersection with speed . The driver notices the intersection’s traffic lights are red and they must stop the vehicle within a distance of .
Using model B and taking reaction time into account, calculate the maximum possible speed of the truck if it is to stop before the intersection.
-
EXM.3.AHL.TZ0.9a:
Use an exponential regression to find the value of and of , correct to 4 decimal places.
-
EXM.3.AHL.TZ0.9b.i:
the number of new people infected on day 6.
-
EXM.3.AHL.TZ0.9b.ii:
the day when the total number of people infected will be greater than 1000.
-
EXM.3.AHL.TZ0.9c:
Use your answer to part (a) to show that the model predicts 16.7 people will be infected on the first day.
-
EXM.3.AHL.TZ0.9d.i:
Explain why the number of degrees of freedom is 2.
-
EXM.3.AHL.TZ0.9d.ii:
Perform a goodness of fit test at the 5% significance level. You should clearly state your hypotheses, the p-value, and your conclusion.
-
EXM.3.AHL.TZ0.9e:
Give two reasons why the prediction in part (b)(ii) might be lower than 14.
-
EXM.3.AHL.TZ0.9f.i:
.
-
EXM.3.AHL.TZ0.9f.ii:
.
-
EXM.3.AHL.TZ0.9f.iii:
.
-
EXM.3.AHL.TZ0.9g:
Hence predict the total number of people infected by this disease after several months.
-
EXM.3.AHL.TZ0.9h:
Use the logistic model to find the day when the rate of increase of people infected is greatest.
-
17M.2.SL.TZ1.T_4a:
Calculate the volume of this pan.
-
17M.2.SL.TZ1.T_4b:
Find the radius of the sphere in cm, correct to one decimal place.
-
17M.2.SL.TZ1.T_4c:
Find the value of .
-
17M.2.SL.TZ1.T_4d:
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.
-
17M.2.SL.TZ1.T_4e:
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.
-
17M.2.SL.TZ1.T_4f:
In the context of this model, state what the value of 19 represents.
-
16N.2.SL.TZ0.T_6a:
Write down a formula for , the surface area to be coated.
-
16N.2.SL.TZ0.T_6b:
Express this volume in .
-
16N.2.SL.TZ0.T_6c:
Write down, in terms of and , an equation for the volume of this water container.
-
16N.2.SL.TZ0.T_6d:
Show that .
-
16N.2.SL.TZ0.T_6e:
Find .
-
16N.2.SL.TZ0.T_6f:
Using your answer to part (e), find the value of which minimizes .
-
16N.2.SL.TZ0.T_6g:
Find the value of this minimum area.
-
16N.2.SL.TZ0.T_6h:
Find the least number of cans of water-resistant material that will coat the area in part (g).
-
19M.1.SL.TZ2.T_13a:
Find the value of .
-
19M.1.SL.TZ2.T_13b:
Find the time, in years, for the population to decrease to 20 turtles.
-
19M.1.SL.TZ2.T_13c:
There is a number beyond which the turtle population will not decrease.
Find the value of . Justify your answer.
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
18N.1.SL.TZ0.S_8b:
Find the equation of the axis of symmetry of the graph of .
-
18N.1.SL.TZ0.S_8c.i:
Write down the value of .
-
18N.1.SL.TZ0.S_8c.ii:
Find the value of .
-
18N.1.SL.TZ0.S_8d:
The graph of a second function, , is obtained by a reflection of the graph of in the -axis, followed by a translation of .
Find the coordinates of the vertex of the graph of .
-
18M.1.SL.TZ1.S_4a.i:
The equation of the axis of symmetry is x = p. Find p.
-
18M.1.SL.TZ1.S_4a.ii:
Hence, show that a = 2.
-
18M.1.SL.TZ2.S_6:
Let , where p ≠ 0. Find Find the number of roots for the equation .
Justify your answer.
-
16N.2.SL.TZ0.S_6a:
Use the model to find the volume of the barrel.
-
16N.2.SL.TZ0.S_6b:
The empty barrel is being filled with water. The volume of water in the barrel after minutes is given by . How long will it take for the barrel to be half-full?
-
16N.1.SL.TZ0.S_1a:
Find the equation of the axis of symmetry of the graph of .
-
16N.1.SL.TZ0.S_1b:
(i) Write down the value of .
(ii) Find the value of .
-
17N.2.SL.TZ0.S_10a:
Show that .
-
17N.2.SL.TZ0.S_10b.i:
Find the coordinates of and of .
-
17N.2.SL.TZ0.S_10b.ii:
Find the equation of .
-
17N.2.SL.TZ0.S_10c:
Show that the distance between the -coordinates of and is .
-
17N.2.SL.TZ0.S_10d:
A saw has a toothed edge which is 300 mm long. Find the number of complete teeth on this saw.
-
17M.2.SL.TZ1.S_8a.i:
How much time is there between the first low tide and the next high tide?
-
17M.2.SL.TZ1.S_8a.ii:
Find the difference in height between low tide and high tide.
-
17M.2.SL.TZ1.S_8b.i:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.ii:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.iii:
Find the value of .
-
17M.2.SL.TZ1.S_8c:
There are two high tides on 12 December 2017. At what time does the second high tide occur?
-
18M.2.SL.TZ2.S_6c:
Find when the seat is 30 m above the ground for the third time.
-
17M.2.SL.TZ2.S_4a:
Find the value of .
-
17M.2.SL.TZ2.S_4b:
Find the value of .
-
17M.2.SL.TZ2.S_4c:
Use the model to find the depth of the water 10 hours after high tide.
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
16N.2.SL.TZ0.S_10a:
(i) Find the value of .
(ii) Show that .
(iii) Find the value of .
-
16N.2.SL.TZ0.S_10b:
(i) Write down the value of .
(ii) Find .
-
16N.2.SL.TZ0.S_10c:
(i) Find .
(ii) Hence or otherwise, find the maximum positive rate of change of .
-
18N.2.SL.TZ0.T_4a:
Sketch the graph of y = f (x), for −4 ≤ x ≤ 3 and −50 ≤ y ≤ 100.
-
18N.2.SL.TZ0.T_4b.i:
Use your graphic display calculator to find the zero of f (x).
-
18N.2.SL.TZ0.T_4b.ii:
Use your graphic display calculator to find the coordinates of the local minimum point.
-
18N.2.SL.TZ0.T_4b.iii:
Use your graphic display calculator to find the equation of the tangent to the graph of y = f (x) at the point (–2, 38.75).
Give your answer in the form y = mx + c.
-
16N.1.SL.TZ0.T_15a:
Write down, and simplify, an expression for the car’s value when Gabriella purchased it.
-
16N.1.SL.TZ0.T_15b:
Find the value of .
-
16N.1.SL.TZ0.T_15c:
Find the value of .
-
16N.2.SL.TZ0.T_1a:
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the -axis and 2 cm to represent 10 points on the -axis.
-
16N.2.SL.TZ0.T_1b:
(i) , the mean number of hours spent on social media;
(ii) , the mean number of IB Diploma points.
-
16N.2.SL.TZ0.T_1c:
Plot the point on your scatter diagram and label this point M.
-
16N.2.SL.TZ0.T_1e:
Write down the equation of the regression line on for these eight male students.
-
16N.2.SL.TZ0.T_1f:
Draw the regression line, from part (e), on your scatter diagram.
-
16N.2.SL.TZ0.T_1g:
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
-
16N.2.SL.TZ0.T_1h:
Write down a reason why this estimate is not reliable.
-
18M.2.SL.TZ1.T_4a:
Find the value of k.
-
18M.2.SL.TZ1.T_4b:
Using your value of k , find f ′(x).
-
18M.2.SL.TZ1.T_4c:
Use your answer to part (b) to show that the minimum value of f(x) is −22 .
-
18M.2.SL.TZ1.T_4e:
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph. -
18M.2.SL.TZ2.T_6a:
Sketch the curve for −1 < x < 3 and −2 < y < 12.
-
18M.2.SL.TZ2.T_6b:
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.State the name of the student who made an incorrect observation.
-
18M.2.SL.TZ2.T_6d:
Find .
-
18M.2.SL.TZ2.T_6f:
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.
-
17M.1.SL.TZ2.T_14a:
Write down the amount of money Jashanti saves per month.
-
17M.1.SL.TZ2.T_14b:
Use your graphic display calculator to find how long it will take for Jashanti to have saved enough money to buy the car.
-
17M.1.SL.TZ2.T_14c:
Calculate how much extra money Jashanti needs.
-
19M.2.SL.TZ1.T_4b.ii:
State the domain of .
-
19M.2.SL.TZ1.T_4d:
Find the distance from the centre of Orangeton to the point at which the road meets the highway.
-
19M.2.SL.TZ1.T_4e:
This straight road crosses the highway and then carries on due north.
State whether the straight road will ever cross the river. Justify your answer.
-
19M.2.SL.TZ2.T_5d:
Find .
-
19M.2.SL.TZ2.T_5e:
Find the gradient of the graph of at .
-
19M.2.SL.TZ2.T_5f:
Find the equation of the tangent line to the graph of at . Give the equation in the form where, , , and .
-
17N.1.SL.TZ0.T_6a:
Use this information to write down an equation involving and .
-
17N.1.SL.TZ0.T_6b:
Use this ratio to write down in terms of .
-
17N.1.SL.TZ0.T_6c:
Find the value of and of .
-
18M.1.SL.TZ2.T_6a:
Find the value of a.
-
18M.1.SL.TZ2.T_6b:
Find the coordinates of R.
-
18M.1.SL.TZ2.T_6c:
Line L3 is parallel to line L2 and passes through the point (2, 3).
Find the equation of line L3. Give your answer in the form y = mx + c.
-
17M.2.SL.TZ1.T_3a:
Calculate .
-
17M.2.SL.TZ1.T_3b:
Sketch the graph of for and .
-
17M.2.SL.TZ1.T_3c:
Write down the equation of the vertical asymptote.
-
17M.2.SL.TZ1.T_3d:
Write down the coordinates of the -intercept.
-
17M.2.SL.TZ1.T_3e:
Write down the possible values of for which and .
-
17M.2.SL.TZ1.T_3f:
Find the solution of .
-
18M.1.SL.TZ1.T_12a:
Using only this information, write down an equation in terms of a and b.
-
18M.1.SL.TZ1.T_12b:
Using this information, write down a second equation in terms of a and b.
-
18M.1.SL.TZ1.T_12c:
Hence find the value of a and of b.
-
18M.1.SL.TZ1.T_12d:
The graph intersects the x-axis at a second point, P.
Find the x-coordinate of P.
-
17N.1.SL.TZ0.T_11c:
Find the value of and of .
-
17M.2.SL.TZ1.T_6a:
Find .
-
17M.2.SL.TZ1.T_6b.i:
Show that .
-
17M.2.SL.TZ1.T_6b.ii:
Find the equation of the tangent to the graph of at . Give your answer in the form .
-
17M.2.SL.TZ1.T_6c:
Use your answer to part (a) and the value of , to find the -coordinates of the stationary points of the graph of .
-
17M.2.SL.TZ1.T_6d.i:
Find .
-
17M.2.SL.TZ1.T_6d.ii:
Hence justify that is decreasing at .
-
17M.2.SL.TZ1.T_6e:
Find the -coordinate of the local minimum.
-
17M.1.SL.TZ1.T_15a:
Write down the value of .
-
17M.1.SL.TZ1.T_15b:
Find the value of and of .
-
17M.1.SL.TZ1.T_15c:
Write down the second -intercept of the function.
-
17M.1.SL.TZ2.T_15:
Consider the following graphs of quadratic functions.

The equation of each of the quadratic functions can be written in the form , where .
Each of the sets of conditions for the constants , and , in the table below, corresponds to one of the graphs above.
Write down the number of the corresponding graph next to each set of conditions.

-
18M.1.SL.TZ2.T_13a:
Find the cost of producing 70 shirts.
-
18M.1.SL.TZ2.T_13b:
Find the value of s.
-
18M.1.SL.TZ2.T_13c:
Find the number of shirts produced when the cost of production is lowest.
-
18M.1.SL.TZ2.T_14a:
Find f'(x)
-
18M.1.SL.TZ2.T_14b:
Find the gradient of the graph of f at .
-
18M.1.SL.TZ2.T_14c:
Find the x-coordinate of the point at which the normal to the graph of f has gradient .
-
17N.1.SL.TZ0.T_15a:
Write down how many kilograms of cheese Maria sells in one week if the price of a kilogram of cheese is 8 EUR.
-
17N.1.SL.TZ0.T_15b:
Find how much Maria earns in one week, from selling cheese, if the price of a kilogram of cheese is 8 EUR.
-
17N.1.SL.TZ0.T_15c:
Write down an expression for in terms of .
-
17N.1.SL.TZ0.T_15d:
Find the price, , that will give Maria the highest weekly profit.
-
18M.1.SL.TZ1.T_9a.i:
Find the number of fruit flies which were placed in the container.
-
18M.1.SL.TZ1.T_9a.ii:
Find the number of fruit flies that are in the container after 6 days.
-
18M.1.SL.TZ1.T_9b:
The maximum capacity of the container is 8000 fruit flies.
Find the number of days until the container reaches its maximum capacity.
-
18M.1.SL.TZ2.T_10a:
Find the value of A.
-
18M.1.SL.TZ2.T_10b:
Interpret what A represents in this context.
-
18M.1.SL.TZ2.T_10c:
Find the time since the experiment began for the bacteria population to be equal to 40A.
-
17N.1.SL.TZ0.T_12a:
Write down what the value of 150 represents in the context of the question.
-
17N.1.SL.TZ0.T_12b:
Find the value of .
-
17N.1.SL.TZ0.T_12c:
Find the total time that the baking tin is in the oven.
-
18N.1.SL.TZ0.T_15c:
Write down the maximum amount of yeast in this solution.
-
17N.2.SL.TZ0.T_5a:
Find the exact value of each of the zeros of .
-
17N.2.SL.TZ0.T_5b.i:
Expand the expression for .
-
17N.2.SL.TZ0.T_5b.ii:
Find .
-
17N.2.SL.TZ0.T_5c:
Use your answer to part (b)(ii) to find the values of for which is increasing.
-
17N.2.SL.TZ0.T_5d:
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
-
17N.2.SL.TZ0.T_5e:
Write down the coordinates of the point of intersection.
-
18M.1.SL.TZ2.T_11a:
Write down the equation of the vertical asymptote.
-
18M.1.SL.TZ2.T_11b:
Write down the equation of the horizontal asymptote.
-
18M.1.SL.TZ2.T_11c:
Calculate the value of x for which f(x) = 0 .
-
17M.2.SL.TZ2.T_6a:
Write down the -intercept of the graph.
-
17M.2.SL.TZ2.T_6b:
Find .
-
17M.2.SL.TZ2.T_6c.i:
Show that .
-
17M.2.SL.TZ2.T_6c.ii:
Find .
-
17M.2.SL.TZ2.T_6d.i:
Write down the -coordinates of these two points;
-
17M.2.SL.TZ2.T_6d.ii:
Write down the intervals where the gradient of the graph of is positive.
-
17M.2.SL.TZ2.T_6e:
Write down the range of .
-
17M.2.SL.TZ2.T_6f:
Write down the number of possible solutions to the equation .
-
17M.2.SL.TZ2.T_6g:
The equation , where , has four solutions. Find the possible values of .
-
17N.1.SL.TZ0.T_14a:
Write down the derivative of .
-
17N.1.SL.TZ0.T_14b:
Find the point on the graph of at which the gradient of the tangent is equal to 6.
-
18N.1.SL.TZ0.T_11a:
Find .
-
18N.1.SL.TZ0.T_11b:
Find the gradient of this tangent at point P.
-
18N.1.SL.TZ0.T_11c:
Find the equation of this tangent. Give your answer in the form y = mx + c.
-
19M.1.SL.TZ2.T_15a:
Find the value of if no vases are sold.
-
19M.1.SL.TZ2.T_15b:
Differentiate .
-
19N.1.SL.TZ0.T_11a:
Write down the number of Elvis impersonators in .
-
19N.1.SL.TZ0.T_11b:
Calculate the time taken for the number of Elvis impersonators to reach .
-
19N.1.SL.TZ0.T_11c:
Calculate the number of Elvis impersonators when .
-
19N.1.SL.TZ0.T_11d:
The world population in is projected to be people.
Use this information to explain why the model for the number of Elvis impersonators is unrealistic.
-
19N.1.SL.TZ0.T_2a:
Write down the initial design fee charged for each order.
-
19N.1.SL.TZ0.T_2b:
Find the total amount charged for an order of T-shirts.
-
19N.1.SL.TZ0.T_2c:
Write down the number of T-shirts in an order for which EnYear charged euros.
-
19N.1.SL.TZ0.T_2d:
An order of T-shirts will be charged the same price by both M-Line and EnYear.
Find the value of .
-
19N.2.SL.TZ0.T_4a:
Find the value of .
-
19N.2.SL.TZ0.T_4b:
Write down the equation for the axis of symmetry of the graph.
-
19N.2.SL.TZ0.T_4c:
Use the symmetry of the graph to show that the second solution is .
-
19N.2.SL.TZ0.T_4d:
Write down the -intercepts of the graph.
-
19N.2.SL.TZ0.T_4e:
On graph paper, draw the graph of for and . Use a scale of to represent unit on the -axis and to represent units on the -axis.
-
19N.2.SL.TZ0.T_4f.i:
Write down the equation of .
-
19N.2.SL.TZ0.T_4f.ii:
Draw the tangent on your graph.
-
19N.2.SL.TZ0.T_4g:
Given and , state whether the function, , is increasing or decreasing at . Give a reason for your answer.
-
20N.2.SL.TZ0.S_4a:
Find .
-
20N.2.SL.TZ0.S_4b.i:
Solve the equation .
-
20N.2.SL.TZ0.S_4b.ii:
Hence or otherwise, given that , find the value of .
-
20N.1.SL.TZ0.T_11a:
Write down the other solution of .
-
20N.1.SL.TZ0.T_11b:
Complete the table below placing a tick (✔) to show whether the unknown parameters and are positive, zero or negative. The row for has been completed as an example.
-
20N.1.SL.TZ0.T_11c:
State the values of for which is decreasing.
-
20N.1.SL.TZ0.T_12a:
Find the value of .
-
20N.1.SL.TZ0.T_12b:
In the context of the model, state what the horizontal asymptote represents.
-
20N.1.SL.TZ0.T_12c:
Find Jean-Pierre’s vertical speed after seconds. Give your answer in .
-
EXN.1.SL.TZ0.2a:
Find an equation which links and .
-
EXN.1.SL.TZ0.2b:
Find, to the nearest USD, the cost of disk that has a radius of cm.
-
EXN.1.SL.TZ0.6a.i:
Find the value of .
-
EXN.1.SL.TZ0.6a.ii:
Find the value of .
-
EXN.1.SL.TZ0.6a.iii:
Find the value of .
-
EXN.1.SL.TZ0.6b:
Find the value of at which the population first reaches .
-
EXN.2.SL.TZ0.6f:
Hence find an expression for .
-
EXN.2.AHL.TZ0.4d:
Find the equation for Jorge’s model.
-
EXN.3.AHL.TZ0.1a:
Use this model to predict the number of fish in the lake when .
-
EXN.3.AHL.TZ0.1b:
Assuming the proportion of marked fish in the second sample is equal to the proportion of marked fish in the lake, show that the estate manager will estimate there are now fish in the lake.
-
21M.1.SL.TZ1.4a:
Find the total cost of buying litres of gas at Leon’s gas station.
-
21M.1.SL.TZ1.4b:
Find .
-
21M.1.SL.TZ1.7a:
Find the value of .
-
21M.1.SL.TZ1.7b:
Use this model to find the percentage of information retained by his students hours after Professor Wei’s lecture.
-
21M.1.SL.TZ1.7c:
State a mathematical reason why Professor Wei might believe this.
-
21M.1.SL.TZ1.7d:
Write down one possible limitation of the domain of the model.
-
21M.1.SL.TZ1.11a:
Show that .
-
21M.1.SL.TZ1.11b:
Sketch the curve of on the axes below showing clearly the point .
-
21M.2.SL.TZ1.2g:
Find the value of when .
-
21M.2.SL.TZ1.2h:
Write down the amplitude of .
-
21M.2.SL.TZ1.5a.i:
Find .
-
21M.2.SL.TZ1.5a.ii:
Hence find the maximum height of the tunnel.
-
21M.2.SL.TZ1.5b:
Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel.
-
21M.2.SL.TZ1.5c.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
-
21M.2.SL.TZ1.5c.ii:
Hence find the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2a.i:
Find .
-
21M.2.AHL.TZ1.2a.ii:
Hence find the maximum height of the tunnel.
-
21M.2.AHL.TZ1.2b.i:
.
-
21M.2.AHL.TZ1.2b.ii:
.
-
21M.2.AHL.TZ1.2c:
Use the trapezoidal rule, with three intervals, to estimate the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2d.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.2d.ii:
Hence find the cross-sectional area of the tunnel.
-
21M.2.AHL.TZ1.4b.i:
Find the equation of the least squares regression quadratic curve for these four points.
-
21M.2.AHL.TZ1.4b.ii:
By considering the gradient of this curve when , explain why it may not be a good model.
-
21M.2.AHL.TZ1.4c:
Find the equation of the new model.
-
21M.1.SL.TZ2.1a.i:
the initial dose of the drug.
-
21M.1.SL.TZ2.1a.ii:
the percentage of the drug that leaves the body each hour.
-
21M.1.SL.TZ2.1b:
Calculate the amount of the drug remaining in the body hours after the injection.
-
21M.1.SL.TZ2.12a:
Find the value of .
-
21M.1.SL.TZ2.12b:
Find the value of
(i) .
(ii) .
(iii) .
-
21M.1.SL.TZ2.12c:
Write down the equation of the axis of symmetry of the graph.
-
21N.1.SL.TZ0.3a:
Write down the value of .
-
21N.1.SL.TZ0.3b:
Find the value of .
-
21N.1.SL.TZ0.13a.i:
Write down the value of .
-
21N.1.SL.TZ0.13a.ii:
Hence form two equations in terms of and .
-
21N.1.SL.TZ0.13a.iii:
Hence find the equation of the quadratic curve.
-
21N.1.SL.TZ0.13b:
Find the area of the shaded region in Irina’s design.
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.AHL.TZ0.2a.i:
maximum value of .
-
21N.2.AHL.TZ0.2a.ii:
minimum value of .
-
21N.2.AHL.TZ0.2b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.AHL.TZ0.2b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.AHL.TZ0.2c.i:
Write down the amplitude of the function.
-
21N.2.AHL.TZ0.2c.ii:
Find the period of the function.
-
21N.2.AHL.TZ0.2d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.AHL.TZ0.2e.i:
Find the height of above the ground when .
-
21N.2.AHL.TZ0.2e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.AHL.TZ0.2f:
The wind speed increases and the blades rotate faster, but still at a constant rate.
Given that point is now higher than for second during each complete rotation, find the time for one complete rotation.
-
22M.3.AHL.TZ1.1b.ii:
Using the data in the table write down the equation for an appropriate non-linear regression model.
-
22M.3.AHL.TZ1.1b.v:
By considering large values of write down one criticism of the model found in (b)(ii).
-
22M.3.AHL.TZ1.1c:
Use your answer from part (b)(ii) to estimate the time taken for the number of infected computers to double.
-
22M.3.AHL.TZ1.1d:
Find in which city, X or Y, the computer virus is spreading more easily. Justify your answer using your results from part (b).
-
22M.1.SL.TZ1.3a:
Write down the height of the ball above the ground at the instant it is hit by the bat.
-
22M.1.SL.TZ1.3b:
Find the value of when the ball hits the ground.
-
22M.1.SL.TZ1.11a:
Find the value of .
-
22M.1.SL.TZ1.11b:
Find the value of .
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.AHL.TZ1.12a:
Find the value of .
-
22M.1.AHL.TZ1.12b:
Find the value of .
-
22M.1.AHL.TZ1.12c:
Find the average number of earthquakes in a year with a magnitude of at least .
-
22M.1.SL.TZ2.9b.i:
Write down the value of .
-
22M.1.SL.TZ2.9b.ii:
Write down three simultaneous equations for and .
-
22M.1.SL.TZ2.9b.iii:
Hence, or otherwise, find the values of and .
-
22M.1.SL.TZ2.9c:
Use the model to determine the total length of time, in years, for which a graduate is expected to be in debt after graduating from university.
-
22M.1.SL.TZ2.12a:
Determine an equation for the axis of symmetry of the parabola that models the archway.
-
22M.1.SL.TZ2.12b:
Determine whether the crate will fit through the archway. Justify your answer.
-
22M.2.SL.TZ1.1a:
Write down one reason why a quadratic function would not be a good model for the number of hours of daylight per day, across a number of years.
-
22M.2.SL.TZ1.1b.i:
the amplitude.
-
22M.2.SL.TZ1.1b.ii:
the period.
-
22M.2.SL.TZ1.1b.iii:
the equation of the principal axis.
-
22M.2.SL.TZ1.1c:
Hence or otherwise find the equation of this model in the form:
-
22M.2.SL.TZ2.4a.i:
.
-
22M.2.SL.TZ2.4a.ii:
.
-
22M.2.SL.TZ2.4a.iii:
.
-
22M.2.SL.TZ2.4b:
Calculate the number of revolutions of the Ferris wheel per ride.
-
22M.2.AHL.TZ2.6c:
Assuming that the ground is horizontal and the ball is not hit by the arrow, find the coordinate of the point where the ball lands.
SL 2.6—Modelling skills
-
SPM.2.SL.TZ0.5a.i:
Write down a second equation to represent Model A, when the speed is .
-
SPM.2.SL.TZ0.5a.ii:
Find the values of and .
-
SPM.2.SL.TZ0.5b:
Find the coordinates of the vertex of the graph of .
-
SPM.2.SL.TZ0.5c:
Using the values in the table and your answer to part (b), sketch the graph of for 0 ≤ ≤ 10 and −10 ≤ ≤ 60, clearly showing the vertex.
-
SPM.2.SL.TZ0.5d:
Hence, identify why Model A may not be appropriate at lower speeds.
-
SPM.2.SL.TZ0.5e:
Use Model B to calculate an estimate for the braking distance at a speed of .
-
SPM.2.SL.TZ0.5f:
Calculate the percentage error in the estimate in part (e).
-
SPM.2.SL.TZ0.5g:
It is found that once a driver realizes the need to stop their vehicle, 1.6 seconds will elapse, on average, before the brakes are engaged. During this reaction time, the vehicle will continue to travel at its original speed.
A truck approaches an intersection with speed . The driver notices the intersection’s traffic lights are red and they must stop the vehicle within a distance of .
Using model B and taking reaction time into account, calculate the maximum possible speed of the truck if it is to stop before the intersection.
-
EXM.2.SL.TZ0.3a:
Show that .
-
EXM.2.SL.TZ0.3b:
Write down two more equations for , and .
-
EXM.2.SL.TZ0.3c:
Solve this system of three equations to find the value of , and .
-
EXM.2.SL.TZ0.3d.i:
when the height of the object is zero.
-
EXM.2.SL.TZ0.3d.ii:
the maximum height of the object.
-
EXM.3.AHL.TZ0.9a:
Use an exponential regression to find the value of and of , correct to 4 decimal places.
-
EXM.3.AHL.TZ0.9b.i:
the number of new people infected on day 6.
-
EXM.3.AHL.TZ0.9b.ii:
the day when the total number of people infected will be greater than 1000.
-
EXM.3.AHL.TZ0.9c:
Use your answer to part (a) to show that the model predicts 16.7 people will be infected on the first day.
-
EXM.3.AHL.TZ0.9d.i:
Explain why the number of degrees of freedom is 2.
-
EXM.3.AHL.TZ0.9d.ii:
Perform a goodness of fit test at the 5% significance level. You should clearly state your hypotheses, the p-value, and your conclusion.
-
EXM.3.AHL.TZ0.9e:
Give two reasons why the prediction in part (b)(ii) might be lower than 14.
-
EXM.3.AHL.TZ0.9f.i:
.
-
EXM.3.AHL.TZ0.9f.ii:
.
-
EXM.3.AHL.TZ0.9f.iii:
.
-
EXM.3.AHL.TZ0.9g:
Hence predict the total number of people infected by this disease after several months.
-
EXM.3.AHL.TZ0.9h:
Use the logistic model to find the day when the rate of increase of people infected is greatest.
-
21N.2.SL.TZ0.3a.i:
maximum value of .
-
21N.2.SL.TZ0.3a.ii:
minimum value of .
-
21N.2.SL.TZ0.3b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.SL.TZ0.3b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.SL.TZ0.3c.i:
Write down the amplitude of the function.
-
21N.2.SL.TZ0.3c.ii:
Find the period of the function.
-
21N.2.SL.TZ0.3d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.SL.TZ0.3e.i:
Find the height of above the ground when .
-
21N.2.SL.TZ0.3e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.SL.TZ0.3f.i:
At any given instant, find the probability that point is visible from Tim’s window.
-
21N.2.SL.TZ0.3f.ii:
The wind speed increases. The blades rotate at twice the speed, but still at a constant rate.
At any given instant, find the probability that Tim can see point from his window. Justify your answer.
-
21N.2.AHL.TZ0.2a.i:
maximum value of .
-
21N.2.AHL.TZ0.2a.ii:
minimum value of .
-
21N.2.AHL.TZ0.2b.i:
Find the time, in seconds, it takes for the blade to make one complete rotation under these conditions.
-
21N.2.AHL.TZ0.2b.ii:
Calculate the angle, in degrees, that the blade turns through in one second.
-
21N.2.AHL.TZ0.2c.i:
Write down the amplitude of the function.
-
21N.2.AHL.TZ0.2c.ii:
Find the period of the function.
-
21N.2.AHL.TZ0.2d:
Sketch the function for , clearly labelling the coordinates of the maximum and minimum points.
-
21N.2.AHL.TZ0.2e.i:
Find the height of above the ground when .
-
21N.2.AHL.TZ0.2e.ii:
Find the time, in seconds, that point is above a height of , during each complete rotation.
-
21N.2.AHL.TZ0.2f:
The wind speed increases and the blades rotate faster, but still at a constant rate.
Given that point is now higher than for second during each complete rotation, find the time for one complete rotation.
-
22M.1.SL.TZ1.3a:
Write down the height of the ball above the ground at the instant it is hit by the bat.
-
22M.1.SL.TZ1.3b:
Find the value of when the ball hits the ground.
-
22M.1.SL.TZ1.5a:
Write down three equations that express the information given above.
-
22M.1.SL.TZ1.5b:
Find the number of each type of ticket sold.
-
22M.1.SL.TZ1.11a:
Find the value of .
-
22M.1.SL.TZ1.11b:
Find the value of .
-
22M.1.SL.TZ1.11c:
Given , find the range for .
-
22M.1.AHL.TZ1.12a:
Find the value of .
-
22M.1.AHL.TZ1.12b:
Find the value of .
-
22M.1.AHL.TZ1.12c:
Find the average number of earthquakes in a year with a magnitude of at least .
-
22M.1.SL.TZ2.4a:
Calculate the pH of the coffee.
-
22M.1.SL.TZ2.4b:
Determine whether the unknown liquid is more or less acidic than the coffee. Justify your answer mathematically.
-
22M.1.SL.TZ2.9b.i:
Write down the value of .
-
22M.1.SL.TZ2.9b.ii:
Write down three simultaneous equations for and .
-
22M.1.SL.TZ2.9b.iii:
Hence, or otherwise, find the values of and .
-
22M.1.SL.TZ2.9c:
Use the model to determine the total length of time, in years, for which a graduate is expected to be in debt after graduating from university.
-
22M.2.SL.TZ1.1b.i:
the amplitude.
-
22M.2.SL.TZ1.1b.ii:
the period.
-
22M.2.SL.TZ1.1b.iii:
the equation of the principal axis.
-
22M.2.SL.TZ1.1c:
Hence or otherwise find the equation of this model in the form:
-
22M.2.SL.TZ2.2e:
Comment on the appropriateness of modelling this scenario with a geometric sequence.
-
22M.2.SL.TZ2.3g:
State one criticism of this interpretation.
-
22M.2.SL.TZ2.4a.i:
.
-
22M.2.SL.TZ2.4a.ii:
.
-
22M.2.SL.TZ2.4a.iii:
.
-
22M.2.SL.TZ2.4b:
Calculate the number of revolutions of the Ferris wheel per ride.
-
22M.2.SL.TZ2.4e.i:
Identify which parameter will change.
-
22M.2.SL.TZ2.4e.ii:
Find the new value of the parameter identified in part (e)(i).
-
22M.2.SL.TZ2.5c.i:
Find the value of .
-
22M.2.AHL.TZ2.7f:
Write down one reason, with reference to the context, to support this decision.
AHL 2.7—Composite functions, finding inverse function incl domain restriction
-
18M.1.AHL.TZ2.H_10a:
Find the inverse function , stating its domain.
-
18M.1.AHL.TZ2.H_10b.i:
Express in the form where A, B are constants.
-
18M.1.AHL.TZ2.H_10b.ii:
Sketch the graph of . State the equations of any asymptotes and the coordinates of any intercepts with the axes.
-
18M.1.AHL.TZ2.H_10c:
The function is defined by , for ≥ 0.
State the domain and range of .
-
18M.2.AHL.TZ2.H_10a.i:
Sketch the graph of for .
-
18M.2.AHL.TZ2.H_10a.ii:
With reference to your graph, explain why is a function on the given domain.
-
18M.2.AHL.TZ2.H_10a.iii:
Explain why has no inverse on the given domain.
-
18M.2.AHL.TZ2.H_10a.iv:
Explain why is not a function for .
-
18M.2.AHL.TZ2.H_10b:
Show that .
-
18M.2.AHL.TZ2.H_10c:
Sketch the graph of for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.
-
18M.2.AHL.TZ2.H_10d.i:
Find and β in terms of .
-
18M.2.AHL.TZ2.H_10d.ii:
Show that + β < −2.
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
18N.3.AHL.TZ0.Hsrg_4a.i:
Find .
-
18N.3.AHL.TZ0.Hsrg_4a.ii:
Find .
-
18N.3.AHL.TZ0.Hsrg_4b:
State with a reason whether or not and commute.
-
18N.3.AHL.TZ0.Hsrg_4c:
Find the inverse of .
-
17N.1.SL.TZ0.S_5a:
Find .
-
17N.1.SL.TZ0.S_5b:
Given that , find the value of .
-
18M.1.SL.TZ1.S_3c:
On the grid above, sketch the graph of f −1.
-
17M.2.SL.TZ2.S_6a:
Show that .
-
17M.2.SL.TZ2.S_6b:
On the following grid, sketch the graph of , for .

-
17M.2.SL.TZ2.S_6c:
The equation has exactly two solutions, for . Find the possible values of .
-
19M.2.SL.TZ1.S_9a:
Find the gradient of .
-
19M.2.SL.TZ1.S_9b:
Find u.
-
19M.2.SL.TZ1.S_9c:
Find the acute angle between and .
-
19M.2.SL.TZ1.S_9d.i:
Find .
-
19M.2.SL.TZ1.S_9d.ii:
Hence, write down .
-
19M.2.SL.TZ1.S_9d.iii:
Hence or otherwise, find the obtuse angle formed by the tangent line to at and the tangent line to at .
-
16N.2.SL.TZ0.S_1a:
Find .
-
16N.2.SL.TZ0.S_1b:
Find .
-
16N.2.SL.TZ0.S_1c:
Solve .
-
21M.1.AHL.TZ2.2a:
Find the range of .
-
21M.1.AHL.TZ2.2b:
Find an expression for the inverse function. The domain is not required.
-
21M.1.AHL.TZ2.2c:
Write down the range of .
-
22M.1.AHL.TZ2.10a:
Find an expression for . You are not required to state a domain.
-
22M.2.AHL.TZ1.6b:
Find the value of and the value of .
AHL 2.8—Transformations of graphs, composite transformations
-
SPM.1.AHL.TZ0.14a.i:
Write down the value of .
-
SPM.1.AHL.TZ0.14a.ii:
Find the value of .
-
SPM.1.AHL.TZ0.14b:
The outer dome of a large cathedral has the shape of a hemisphere of diameter 32 m, supported by vertical walls of height 17 m. It is also supported by an inner dome which can be modelled by rotating the curve through 360° about the -axis between = 0 and = 33, as indicated in the diagram.
Find the volume of the space between the two domes.
-
19M.1.AHL.TZ2.H_11a:
Describe the transformation by which is transformed to .
-
19M.1.AHL.TZ2.H_11b:
State the range of .
-
19M.1.AHL.TZ2.H_11c:
Sketch the graphs of and on the same axes, clearly stating the points of intersection with any axes.
-
19M.1.AHL.TZ2.H_11d:
Find the coordinates of P.
-
19M.1.AHL.TZ2.H_11e:
The tangent to at P passes through the origin (0, 0).
Determine the value of .
-
18N.1.AHL.TZ0.H_3a:
For , sketch the graph of . Indicate clearly the maximum and minimum values of the function.
-
18N.1.AHL.TZ0.H_3b:
Write down the least value of such that has an inverse.
-
18N.1.AHL.TZ0.H_3c.i:
For the value of found in part (b), write down the domain of .
-
18N.1.AHL.TZ0.H_3c.ii:
For the value of found in part (b), find an expression for .
-
19M.1.AHL.TZ2.H_3:
Consider the function , .
The graph of is translated two units to the left to form the function .
Express in the form where , , , , .
-
19M.1.AHL.TZ1.H_10a.i:
Find the remainder when is divided by .
-
19M.1.AHL.TZ1.H_10a.ii:
Find the remainder when is divided by .
-
19M.1.AHL.TZ1.H_10b:
Prove that has only one real zero.
-
19M.1.AHL.TZ1.H_10c:
Write down the transformation that will transform the graph of onto the graph of .
-
19M.1.AHL.TZ1.H_10d:
The random variable follows a Poisson distribution with a mean of and .
Find the value of .
-
19M.2.AHL.TZ1.H_10a:
Write down the maximum and minimum value of .
-
19M.2.AHL.TZ1.H_10b:
Write down two transformations that will transform the graph of onto the graph of .
-
19M.2.AHL.TZ1.H_10c:
Sketch the graph of for 0 ≤ ≤ 0.02 , showing clearly the coordinates of the first maximum and the first minimum.
-
19M.2.AHL.TZ1.H_10d:
Find the total time in the interval 0 ≤ ≤ 0.02 for which ≥ 3.
-
19M.2.AHL.TZ1.H_10e:
Find (0.007).
-
19M.2.AHL.TZ1.H_10f:
With reference to your graph of explain why > 0 for all > 0.
-
19M.2.AHL.TZ1.H_10g:
Given that can be written as where , , , > 0, use your graph to find the values of , , and .
-
18M.1.SL.TZ2.S_5a:
On the same axes, sketch the graph of .
-
18M.1.SL.TZ2.S_5b:
Another function, , can be written in the form . The following diagram shows the graph of .
Write down the value of a and of b.
-
18N.1.SL.TZ0.S_8b:
Find the equation of the axis of symmetry of the graph of .
-
18N.1.SL.TZ0.S_8c.i:
Write down the value of .
-
18N.1.SL.TZ0.S_8c.ii:
Find the value of .
-
18N.1.SL.TZ0.S_8d:
The graph of a second function, , is obtained by a reflection of the graph of in the -axis, followed by a translation of .
Find the coordinates of the vertex of the graph of .
-
19M.1.SL.TZ2.S_4a.i:
Find the -intercept of the graph of .
-
19M.1.SL.TZ2.S_4a.ii:
Find the -intercept of the graph of .
-
19M.1.SL.TZ2.S_4b:
Find the -intercept of the graph of .
-
19M.1.SL.TZ2.S_4c:
Describe the transformation .
-
19M.2.SL.TZ1.S_8a:
The range of is ≤ ≤ . Find and .
-
19M.2.SL.TZ1.S_8b:
Find the range of .
-
19M.2.SL.TZ1.S_8c.i:
Find the value of and of .
-
19M.2.SL.TZ1.S_8c.ii:
Find the period of .
-
19M.2.SL.TZ1.S_8d:
The equation has two solutions where ≤ ≤ . Find both solutions.
-
20N.1.SL.TZ0.S_10a.i:
Find in terms of and .
-
20N.1.SL.TZ0.S_10a.ii:
Show that the equation of is .
-
20N.1.SL.TZ0.S_10b:
Find the area of triangle in terms of .
-
20N.1.SL.TZ0.S_10c:
The graph of is translated by to give the graph of .
In the following diagram:- point lies on the graph of
- points , and lie on the vertical asymptote of
- points and lie on the horizontal asymptote of
- point lies on the -axis such that is parallel to .
Line is the tangent to the graph of at , and passes through and .
Given that triangle and rectangle have equal areas, find the gradient of in terms of .
-
EXN.1.AHL.TZ0.8b:
Write down a sequence of transformations that will transform the graph of onto the graph of .
-
21M.1.AHL.TZ1.17:
The graph of the function is translated by so that it then passes through the points and .
Find the value of and the value of .
-
21N.1.AHL.TZ0.10a:
Find .
-
21N.1.AHL.TZ0.10b:
On the same set of axes draw the graph of , showing any intercepts and asymptotes.
-
22M.2.AHL.TZ1.6b:
Find the value of and the value of .
-
22M.2.AHL.TZ2.6e:
Determine the two positions where the path of the arrow intersects the path of the ball.
-
22M.2.AHL.TZ2.6f:
Determine the time when the arrow should be released to hit the ball before the ball reaches its maximum height.
AHL 2.9—HL modelling functions
-
EXM.2.AHL.TZ0.13a:
Calculate her distance after 8 minutes. Give your answer in km, correct to 3 decimal places.
-
EXM.2.AHL.TZ0.13b:
Find the value of , , and .
-
EXM.2.AHL.TZ0.13c.i:
the distance she runs in 20 minutes.
-
EXM.2.AHL.TZ0.13c.ii:
her maximum speed, in ms–1.
-
EXM.3.AHL.TZ0.9a:
Use an exponential regression to find the value of and of , correct to 4 decimal places.
-
EXM.3.AHL.TZ0.9b.i:
the number of new people infected on day 6.
-
EXM.3.AHL.TZ0.9b.ii:
the day when the total number of people infected will be greater than 1000.
-
EXM.3.AHL.TZ0.9c:
Use your answer to part (a) to show that the model predicts 16.7 people will be infected on the first day.
-
EXM.3.AHL.TZ0.9d.i:
Explain why the number of degrees of freedom is 2.
-
EXM.3.AHL.TZ0.9d.ii:
Perform a goodness of fit test at the 5% significance level. You should clearly state your hypotheses, the p-value, and your conclusion.
-
EXM.3.AHL.TZ0.9e:
Give two reasons why the prediction in part (b)(ii) might be lower than 14.
-
EXM.3.AHL.TZ0.9f.i:
.
-
EXM.3.AHL.TZ0.9f.ii:
.
-
EXM.3.AHL.TZ0.9f.iii:
.
-
EXM.3.AHL.TZ0.9g:
Hence predict the total number of people infected by this disease after several months.
-
EXM.3.AHL.TZ0.9h:
Use the logistic model to find the day when the rate of increase of people infected is greatest.
-
17M.2.SL.TZ1.S_8a.i:
How much time is there between the first low tide and the next high tide?
-
17M.2.SL.TZ1.S_8a.ii:
Find the difference in height between low tide and high tide.
-
17M.2.SL.TZ1.S_8b.i:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.ii:
Find the value of ;
-
17M.2.SL.TZ1.S_8b.iii:
Find the value of .
-
17M.2.SL.TZ1.S_8c:
There are two high tides on 12 December 2017. At what time does the second high tide occur?
-
18M.2.SL.TZ1.S_10a:
Find the coordinates of A.
-
18M.2.SL.TZ1.S_10b.i:
For the graph of , write down the amplitude.
-
18M.2.SL.TZ1.S_10b.ii:
For the graph of , write down the period.
-
18M.2.SL.TZ1.S_10c:
Hence, write in the form .
-
18M.2.SL.TZ1.S_10d:
Find the maximum speed of the ball.
-
18M.2.SL.TZ1.S_10e:
Find the first time when the ball’s speed is changing at a rate of 2 cm s−2.
-
18M.2.SL.TZ2.S_6c:
Find when the seat is 30 m above the ground for the third time.
-
20N.2.SL.TZ0.S_8a.i:
Find the height of point above the ground.
-
20N.2.SL.TZ0.S_8a.ii:
Calculate the number of seconds it takes for the water wheel to complete one rotation.
-
20N.2.SL.TZ0.S_8a.iii:
Hence find the number of rotations the water wheel makes in one hour.
-
20N.2.SL.TZ0.S_8b:
Find .
-
20N.2.SL.TZ0.S_8c:
Find .
-
20N.2.SL.TZ0.S_8d:
Determine the rate of change of when the top of the bucket is at .
-
EXN.1.AHL.TZ0.8b:
Write down a sequence of transformations that will transform the graph of onto the graph of .
-
EXN.3.AHL.TZ0.1g.i:
Assuming a carrying capacity of use the given values of and to calculate the parameters and .
-
EXN.3.AHL.TZ0.1g.ii:
Use these parameters to calculate the value of predicted by this model.
-
EXN.3.AHL.TZ0.1h:
Comment on the likelihood of the fish population reaching .
-
21M.3.AHL.TZ1.1a:
Show that .
-
21M.3.AHL.TZ1.1b:
Find the angle through which Mars rotates on its axis each hour.
-
21M.3.AHL.TZ1.1c.i:
Show that the maximum value of , correct to three significant figures.
-
21M.3.AHL.TZ1.1c.ii:
Find the minimum value of .
-
21M.3.AHL.TZ1.1d.i:
the maximum value of .
-
21M.3.AHL.TZ1.1d.ii:
the minimum value of .
-
21M.3.AHL.TZ1.1e:
Hence show that , correct to two significant figures.
-
21M.3.AHL.TZ1.1f:
Find the value of .
-
21M.3.AHL.TZ1.1g:
Find the value of .
-
22M.3.AHL.TZ1.1f.ii:
The solution to the differential equation is given by
where is a constant.
Using your answer to part (f)(i), estimate the percentage of computers in city X that are expected to have been infected by the virus over a long period of time.
-
22M.1.AHL.TZ1.17:
A function is of the form . Part of the graph of is shown.
The points and have coordinates and , and lie on .
The point is a local maximum and the point is a local minimum.
Find the value of , of and of .
AHL 2.10—Scaling large numbers, log-log graphs
-
SPM.1.AHL.TZ0.18:
The rate, , of a chemical reaction at a fixed temperature is related to the concentration of two compounds, and , by the equation
, where , , .
A scientist measures the three variables three times during the reaction and obtains the following values.
Find , and .
-
EXM.1.AHL.TZ0.13a:
Find the equation of the straight line, giving your answer in the form , where .
-
EXM.1.AHL.TZ0.13b.i:
a formula for in terms of .
-
EXM.1.AHL.TZ0.13b.ii:
the value of when .
-
EXM.1.AHL.TZ0.14:
It is believed that two variables, and are related by the equation , where . Experimental values of and are obtained. A graph of against shows a straight line passing through (−1.7, 4.3) and (7.1, 17.5).
Find the value of and of .
-
EXM.1.AHL.TZ0.15a:
Show that .
-
EXM.1.AHL.TZ0.15b:
Find the equation of the regression line of on .
-
EXM.1.AHL.TZ0.15c.i:
find the value of and of .
-
EXM.1.AHL.TZ0.15c.ii:
predict the temperature of the metal rod after 3 minutes.
-
EXM.3.AHL.TZ0.7a.i:
Use the trapezoidal rule to find an estimate for the area.
-
EXM.3.AHL.TZ0.7a.ii:
With reference to the shape of the graph, explain whether your answer to part (a)(i) will be an over-estimate or an underestimate of the area.
-
EXM.3.AHL.TZ0.7b.i:
Use all the coordinates in the table to find the equation of the least squares cubic regression curve.
-
EXM.3.AHL.TZ0.7b.ii:
Write down the coefficient of determination.
-
EXM.3.AHL.TZ0.7c.i:
Write down an expression for the area enclosed by the cubic function, the -axis, the -axis and the line .
-
EXM.3.AHL.TZ0.7c.ii:
Find the value of this area.
-
EXM.3.AHL.TZ0.7d.i:
Show that .
-
EXM.3.AHL.TZ0.7d.ii:
Hence explain how a straight line graph could be drawn using the coordinates in the table.
-
EXM.3.AHL.TZ0.7d.iii:
By finding the equation of a suitable regression line, show that and .
-
EXM.3.AHL.TZ0.7d.iv:
Hence find the area enclosed by the exponential function, the -axis, the -axis and the line .
-
EXN.1.AHL.TZ0.12a:
Explain why this graph indicates that is inversely proportional to .
-
EXN.1.AHL.TZ0.12b:
Find the equation of the least squares regression line of against .
-
EXN.1.AHL.TZ0.12c.i:
Use your answer to part (b) to write down the value of to the nearest integer.
-
EXN.1.AHL.TZ0.12c.ii:
Find an expression for in terms of .
-
21N.1.AHL.TZ0.12a:
Use the data in the second table to find the value of and the value of for the regression line, .
-
21N.1.AHL.TZ0.12b:
Assuming that the model found in part (a) remains valid, estimate the percentage of trees in stock when .
-
22M.2.AHL.TZ2.4c:
(i) the gradient of this line in terms of ;
(ii) the -intercept of this line in terms of .
-
22M.2.AHL.TZ2.4d:
Find the equation of the regression line for on .
