| Date | November 2017 | Marks available | 3 | Reference code | 17N.2.SL.TZ0.T_5 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Find | Question number | T_5 | Adapted from | N/A |
Question
A function is given by .
The graph of the function intersects the graph of .
Find the exact value of each of the zeros of .
Expand the expression for .
Find .
Use your answer to part (b)(ii) to find the values of for which is increasing.
Draw the graph of for and . Use a scale of 2 cm to represent 1 unit on the -axis and 1 cm to represent 5 units on the -axis.
Write down the coordinates of the point of intersection.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(A1)(A1)(A1)
Note: Award (A1) for –1 and each exact value seen. Award at most (A1)(A0)(A1) for use of 2.23606… instead of .
[3 marks]
(A1)
Notes: The expansion may be seen in part (b)(ii).
[1 mark]
(A1)(ft)(A1)(ft)(A1)(ft)
Notes: Follow through from part (b)(i). Award (A1)(ft) for each correct term. Award at most (A1)(ft)(A1)(ft)(A0) if extra terms are seen.
[3 marks]
(M1)
Notes: Award (M1) for their . Accept equality or weak inequality.
(A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for correct endpoints, (A1)(ft) for correct weak or strict inequalities. Follow through from part (b)(ii). Do not award any marks if there is no answer in part (b)(ii).
[3 marks]
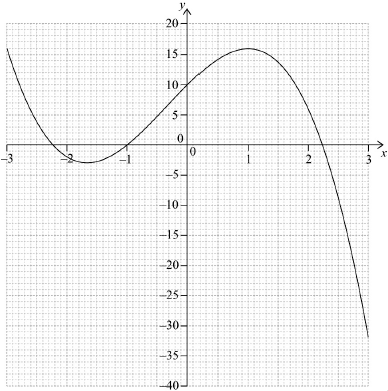 (A1)(A1)(ft)(A1)(ft)(A1)
(A1)(A1)(ft)(A1)(ft)(A1)
Notes: Award (A1) for correct scale; axes labelled and drawn with a ruler.
Award (A1)(ft) for their correct -intercepts in approximately correct location.
Award (A1) for correct minimum and maximum points in approximately correct location.
Award (A1) for a smooth continuous curve with approximate correct shape. The curve should be in the given domain.
Follow through from part (a) for the -intercepts.
[4 marks]
(G1)(ft)(G1)(ft)
Notes: Award (G1) for 1.49 and (G1) for 13.9 written as a coordinate pair. Award at most (G0)(G1) if parentheses are missing. Accept and . Follow through from part (b)(i).
[2 marks]

