| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.AHL.TZ1.H_12 |
| Level | Additional Higher Level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Find | Question number | H_12 | Adapted from | N/A |
Question
Consider
The function is defined by
The function is defined by .
Find the largest possible domain for to be a function.
Sketch the graph of showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why is an even function.
Explain why the inverse function does not exist.
Find the inverse function and state its domain.
Find .
Hence, show that there are no solutions to ;
Hence, show that there are no solutions to .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(M1)
or A1
[2 marks]
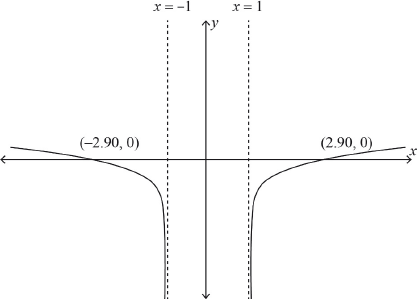
shape A1
and A1
-intercepts A1
[3 marks]
EITHER
is symmetrical about the -axis R1
OR
R1
[1 mark]
EITHER
is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
M1
M1
A1A1
[4 marks]
M1A1
A1
[3 marks]
M1
which is not in the domain of (hence no solutions to ) R1
[2 marks]
M1
as so no solutions to R1
Note: Accept: equation has no solutions.
[2 marks]