| Date | November 2017 | Marks available | 4 | Reference code | 17N.1.AHL.TZ0.H_6 |
| Level | Additional Higher Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Sketch | Question number | H_6 | Adapted from | N/A |
Question
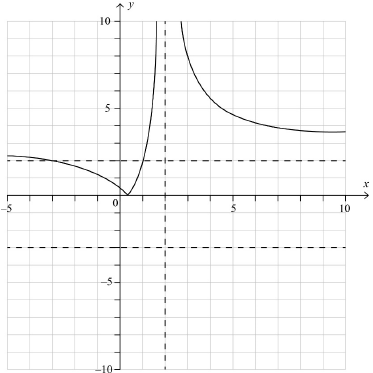
Sketch the graph of , showing clearly any asymptotes and stating the coordinates of any points of intersection with the axes.

Hence or otherwise, solve the inequality .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
correct vertical asymptote A1
shape including correct horizontal asymptote A1
A1
A1
Note: Accept and marked on the axes.
[4 marks]
METHOD 1
(M1)
A1
(M1)
Note: Award this M1 for the line above or a correct sketch identifying a second critical value.
A1
solution is A1
METHOD 2
(M1)A1
A1
(M1)
solution is A1
METHOD 3
consider (M1)
Note: Also allow consideration of “>” or “=” for the awarding of the M mark.
recognition of critical value at A1
consider (M1)
Note: Also allow consideration of “>” or “=” for the awarding of the M mark.
recognition of critical value at A1
solution is A1
[5 marks]