| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.AHL.TZ1.H_11 |
| Level | Additional Higher Level | Paper | Paper 1 | Time zone | Time zone 1 |
| Command term | Question number | H_11 | Adapted from | N/A |
Question
Consider the function .
Express in the form .
Factorize .
Sketch the graph of , indicating on it the equations of the asymptotes, the coordinates of the -intercept and the local maximum.
Show that .
Hence find the value of if .
Sketch the graph of .
Determine the area of the region enclosed between the graph of , the -axis and the lines with equations and .
Markscheme
A1
[1 mark]
A1
[1 mark]
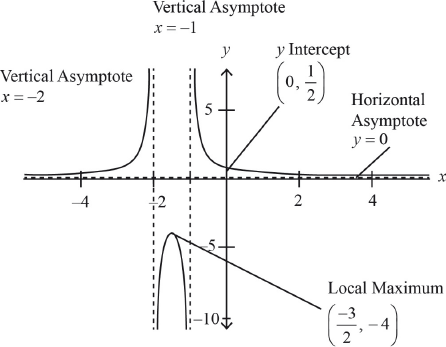
A1 for the shape
A1 for the equation
A1 for asymptotes and
A1 for coordinates
A1 -intercept
[5 marks]
M1
AG
[1 mark]
A1
M1
M1A1
[4 marks]
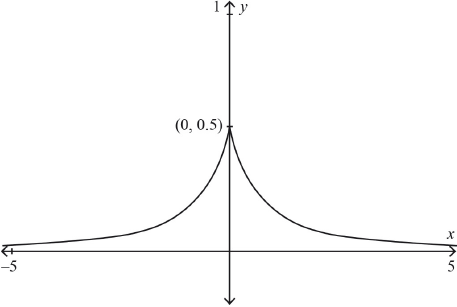
symmetry about the -axis M1
correct shape A1
Note: Allow FT from part (b).
[2 marks]
(M1)(A1)
A1
Note: Do not award FT from part (e).
[3 marks]