| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.SL.TZ2.T_13 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 2 |
| Command term | Write down | Question number | T_13 | Adapted from | N/A |
Question
The diagram shows part of the graph of a function . The graph passes through point .
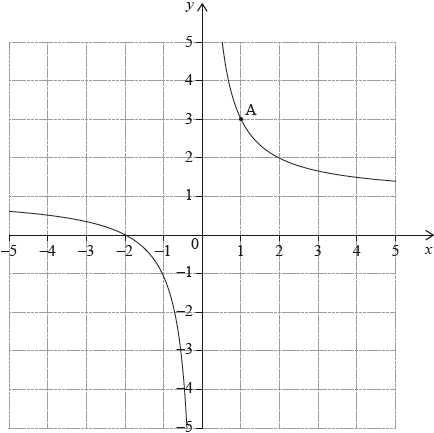
The tangent to the graph of at A has equation . Let be the normal to the graph of at A.
Write down the value of .
Find the equation of . Give your answer in the form where , , .
Draw the line on the diagram above.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
3 (A1) (C1)
Notes: Accept
[1 mark]
OR (A1)(A1)
Note: Award (A1) for correct gradient, (A1) for correct substitution of in the equation of line.
or any integer multiple (A1)(ft) (C3)
Note: Award (A1)(ft) for their equation correctly rearranged in the indicated form.
The candidate’s answer must be an equation for this mark.
[3 marks]
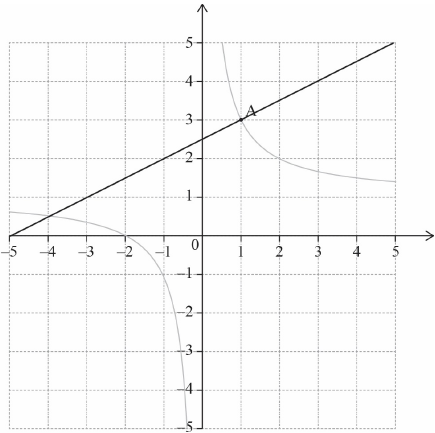 (M1)(A1)(ft) (C2)
(M1)(A1)(ft) (C2)
Note: Award M1) for a straight line, with positive gradient, passing through , (A1)(ft) for line (or extension of their line) passing approximately through 2.5 or their intercept with the -axis.
[2 marks]

