| Date | November 2021 | Marks available | 3 | Reference code | 21N.1.SL.TZ0.13 |
| Level | Standard Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Find | Question number | 13 | Adapted from | N/A |
Question
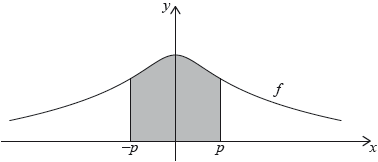
Irina uses a set of coordinate axes to draw her design of a window. The base of the window is on the -axis, the upper part of the window is in the form of a quadratic curve and the sides are vertical lines, as shown on the diagram. The curve has end points and and its vertex is . Distances are measured in centimetres.
The quadratic curve can be expressed in the form for .
Write down the value of .
Hence form two equations in terms of and .
Hence find the equation of the quadratic curve.
Find the area of the shaded region in Irina’s design.
Markscheme
A1
[1 mark]
A1
A1
Note: Award A1 for each equivalent expression or A1 for the use of the axis of symmetry formula to find or from use of derivative. Award A0A1 for and .
[2 marks]
A1A1
Note: Award A1A0 if one term is incorrect, A0A0 if two or more terms are incorrect. Award at most A1A0 if correct and values are seen but answer not expressed as an equation.
[2 marks]
recognizing the need to integrate their expression (M1)
(A1)
Note: Award (A1) for correct integral, including limits. Condone absence of .
A1
[3 marks]
Examiners report
Generally, the responses were good for this last question on the paper. The main issue here was to not give the two equations in part (a)(ii) with simplified coefficients of and . Several candidates understood what was required but left their answers with and un-simplified and lost marks. Some candidates used the coordinates to substitute in the equation with an incorrect equation of . Candidates were successful at writing the equations in part (a)(iii). In part (b), most candidates realized that they had to use integration to find the area of the shaded region and, for the most part, were able to find a correct value for the area using either the correct equation or their obtained equation from the previous part. A common error was to integrate between and instead of and .
Generally, the responses were good for this last question on the paper. The main issue here was to not give the two equations in part (a)(ii) with simplified coefficients of and . Several candidates understood what was required but left their answers with and un-simplified and lost marks. Some candidates used the coordinates to substitute in the equation with an incorrect equation of . Candidates were successful at writing the equations in part (a)(iii). In part (b), most candidates realized that they had to use integration to find the area of the shaded region and, for the most part, were able to find a correct value for the area using either the correct equation or their obtained equation from the previous part. A common error was to integrate between and instead of and .
Generally, the responses were good for this last question on the paper. The main issue here was to not give the two equations in part (a)(ii) with simplified coefficients of and . Several candidates understood what was required but left their answers with and un-simplified and lost marks. Some candidates used the coordinates to substitute in the equation with an incorrect equation of . Candidates were successful at writing the equations in part (a)(iii). In part (b), most candidates realized that they had to use integration to find the area of the shaded region and, for the most part, were able to find a correct value for the area using either the correct equation or their obtained equation from the previous part. A common error was to integrate between and instead of and .
Generally, the responses were good for this last question on the paper. The main issue here was to not give the two equations in part (a)(ii) with simplified coefficients of and . Several candidates understood what was required but left their answers with and un-simplified and lost marks. Some candidates used the coordinates to substitute in the equation with an incorrect equation of . Candidates were successful at writing the equations in part (a)(iii). In part (b), most candidates realized that they had to use integration to find the area of the shaded region and, for the most part, were able to find a correct value for the area using either the correct equation or their obtained equation from the previous part. A common error was to integrate between and instead of and .