Question 1a
A mass-spring system has been set up horizontally on the lab bench, so that the mass can oscillate.
The time period of the mass is given by the equation:
T = 2π
[1]
(ii) Outline the condition under which the equation can be applied.
[1]
Question 1b
Question 1c
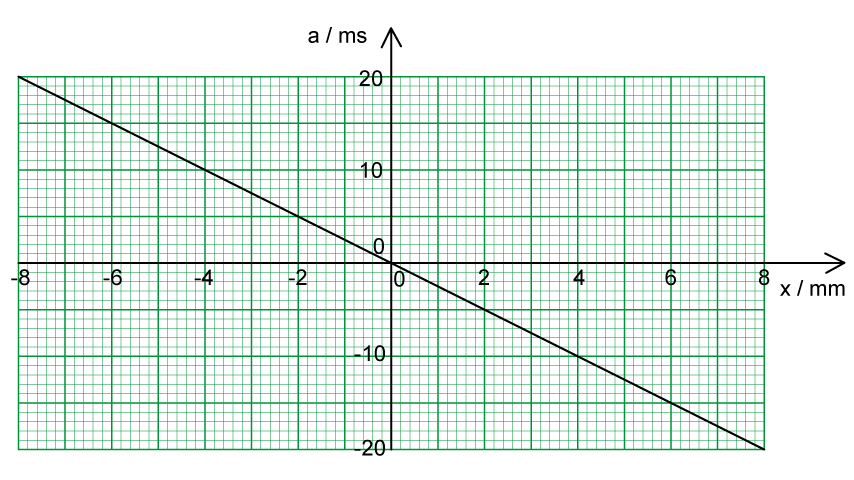
A new mass of m = 50 g replaces the 0.7 kg mass and is now attached to the mass-spring system.
The graph shows the variation with time of the velocity of the block.