10.2.5 Skills: Chi-squared Test

Use of a chi-squared test on data from dihybrid crosses

• The difference between expected and observed results in experiments can be statistically significant or insignificant (happened by chance)
• If the difference between results is statistically significant it can suggest that something else is happening in the experiment that isn’t being accounted for
  • For example, linkage between genes
• A statistical test called the chi-squared test determines whether there is a significant difference between the observed and expected results in an experiment
• The chi-squared test is completed when the data is categorical (data that can be grouped)

Calculating chi-squared values

• Obtain the expected and observed results for the experiment
• Calculate the difference between each set of results
• Square each difference (as it is irrelevant whether the difference is positive or negative)
• Divide each squared difference by the expected value and get a sum of these answers to obtain the chi-squared value

Analysing chi-squared values

• To work out what the chi-squared value means, a table that relates chi-squared values to probabilities is used
• If the chi-squared value represents a larger probability than the critical probability then it can be stated that the differences between the expected and observed results are due to chance
• If it represents a smaller probability than the critical probability then the differences in results are significant and something else may be causing the differences
• To determine the critical probability biologists generally use a probability of 0.05 (they allow that chance will cause five out of every 100 experiments to be different)
• The number of comparisons made must also be taken into account when determining the critical probability. This is known as the degrees of freedom

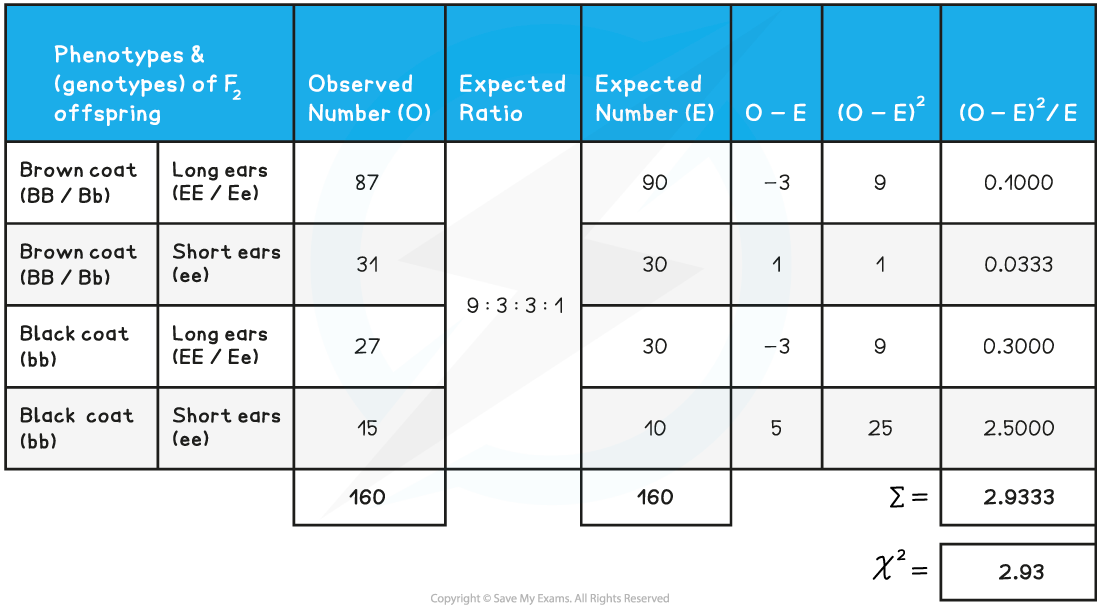
• The expected number of each phenotype is the fraction of the total number of rabbits governed by the 9:3:3:1 ratio
• These are ⁹/₁₆, ³/₁₆, ³/₁₆ and ¹/₁₆ of 160, respectively
• In order to understand what this chi-squared value of 2.93 says about the data, a table relating chi-squared values to probability is needed

• The chi-squared table displays the probabilities that the differences between expected and observed are due to chance
• The degrees of freedom can be worked out from the results. It is calculated by subtracting one from the number of classes
• In this example, there are four phenotypes which means four classes, 4 – 1 = 3
• This means that the values in the third row are important for comparison
• For this experiment, there is a critical probability of 0.05
• This means that 7.82 is the value used for comparison
• The chi-squared value from the results (2.93) is much smaller than 7.82
• 2.93 would be located somewhere to the left-hand side of the table, representing a probability much greater than 0.1
• This means that there is no significant difference between the expected and observed results, any differences that do occur are due to chance

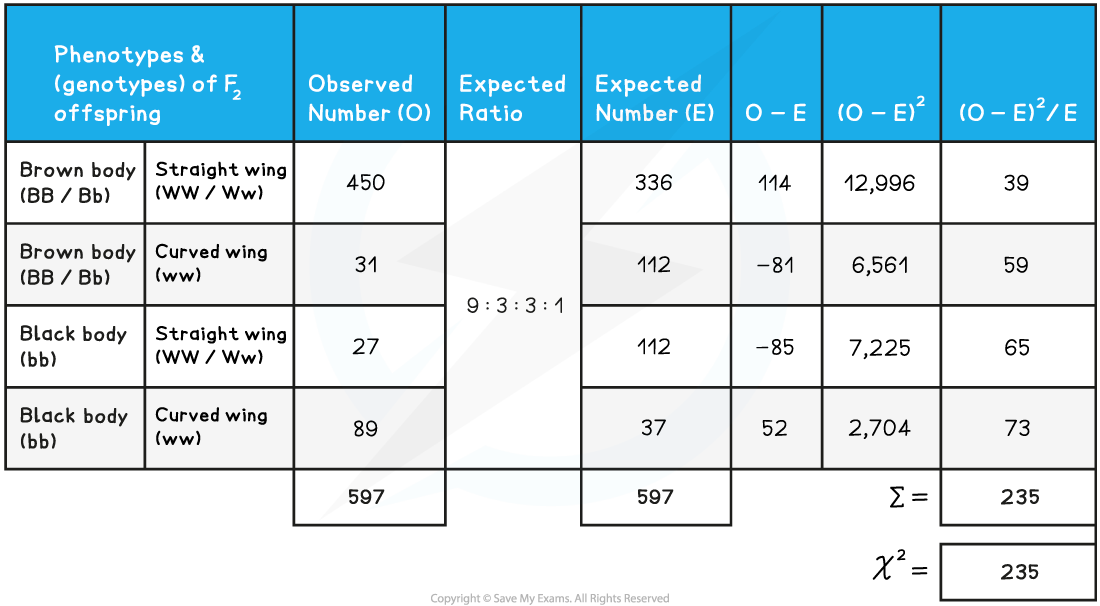
• The expected number of each phenotype is the fraction of the total number of flies governed by the 9:3:3:1 ratio
• These are ⁹/₁₆, ³/₁₆, ³/₁₆ and ¹/₁₆ of 597, respectively
• In order to understand what this chi-squared value of 235 says about the data, a table relating chi-squared values to probability is needed

• The chi-squared table displays the probabilities that the differences between expected and observed are due to chance
• The degrees of freedom can be worked out from the results. It is calculated by subtracting one from the number of classes
• In this example, there are also four phenotypes which means four classes, 4 – 1 = 3
• This means that the values in the third row are important for comparison
• For this experiment, there is a critical probability of 0.05
• This means that 7.82 is the value used for comparison
• The chi-squared value from the results (235) is much greater than 7.82
• 235 would be located somewhere off the far right of the table, representing a very small probability, much less than 0.001
• This means that there is a significant difference between the expected and observed results, any differences that do occur are due to a factor other than chance
• In this case, that factor is (autosomal) gene linkage

Conclusion

• The alleles for black/brown body colour and straight/curved wings are linked, ie. carried on the same chromosome (autosome)