| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ1.7 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
The following diagram shows part of the graph of \(f(x) = - 2{x^3} + 5.1{x^2} + 3.6x - 0.4\).
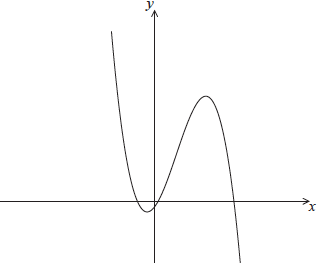
Find the coordinates of the local minimum point.
The graph of \(f\) is translated to the graph of \(g\) by the vector \(\left( {\begin{array}{*{20}{c}} 0 \\ k \end{array}} \right)\). Find all values of \(k\) so that \(g(x) = 0\) has exactly one solution.
Markscheme
\(( - 0.3,{\text{ }} - 0.967)\)
\(x = - 0.3\) (exact), \(y = - 0.967\) (exact) A1A1 N2
[2 marks]
\(y\)-coordinate of local maximum is \(y = 11.2\) (A1)
negating the \(y\)-coordinate of one of the max/min (M1)
eg\(\;\;\;y = 0.967,{\text{ }}y = - 11.2\)
recognizing that the solution set has two intervals R1
eg\(\;\;\;\)two answers,
\(k < - 11.2,{\text{ }}k > 0.967\) A1A1 N3N2
[5 marks]
Notes: If working shown, do not award the final mark if strict inequalities are not used.
If no working shown, award N2 for \(k \le - 11.2\) or N1 for \(k \ge 0.967\)
Total [7 marks]
Examiners report
The coordinates of the minimum point was correctly given by most candidates, although some opted for an analytical approach which was often futile and time consuming.
In part (b), few students appreciated that the solution set consisted of two intervals often giving only one correct interval or equalities. The most common, incorrect approach was an attempt to use the discriminant.

