| Date | November 2016 | Marks available | 5 | Reference code | 16N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 2 | Adapted from | N/A |
Question
Let \(f(x) = 0.225{x^3} - 2.7x\), for \( - 3 \leqslant x \leqslant 3\). There is a local minimum point at A.
On the following grid,
Find the coordinates of A.
[2]
a.
(i) sketch the graph of \(f\), clearly indicating the point A;
(ii) sketch the tangent to the graph of \(f\) at A.
[5]
b.
Markscheme
\({\text{A }}(2,{\text{ }}-3.6)\) A1A1 N2
[2 marks]
a.
(i) (ii)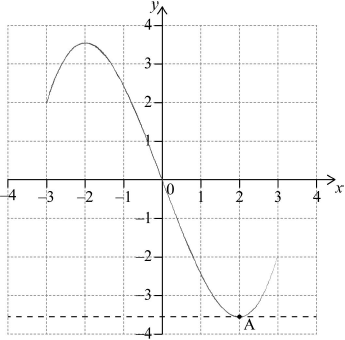 
A1
A1A1A1 N4
A1 N1
Notes: (i) Award A1 for correct cubic shape with correct curvature.
Only if this A1 is awarded, award the following:
A1 for passing through their point A and the origin,
A1 for endpoints,
A1 for maximum.
(ii) Award A1 for horizontal line through their A.
[5 marks]
b.
Examiners report
[N/A]
a.
[N/A]
b.
Syllabus sections
Topic 2 - Functions and equations » 2.2 » Investigation of key features of graphs, such as maximum and minimum values, intercepts, horizontal and vertical asymptotes, symmetry, and consideration of domain and range.
Show 86 related questions
