| Date | November 2009 | Marks available | 2 | Reference code | 09N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \sqrt x \) . Line L is the normal to the graph of f at the point (4, 2) .
In the diagram below, the shaded region R is bounded by the x-axis, the graph of f and the line L .
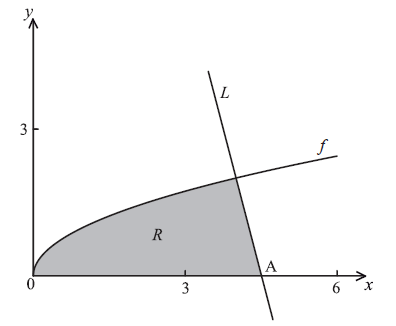
Show that the equation of L is \(y = - 4x + 18\) .
Point A is the x-intercept of L . Find the x-coordinate of A.
Find an expression for the area of R .
The region R is rotated \(360^\circ \) about the x-axis. Find the volume of the solid formed, giving your answer in terms of \(\pi \) .
Markscheme
finding derivative (A1)
e.g. \(f'(x) = \frac{1}{2}{x^{\frac{1}{2}}},\frac{{1}}{{2\sqrt x }}\)
correct value of derivative or its negative reciprocal (seen anywhere) A1
e.g. \(\frac{1}{{2\sqrt 4 }}\) , \(\frac{1}{4}\)
gradient of normal = \(\frac{1}{{{\text{gradient of tangent}}}}\) (seen anywhere) A1
e.g. \( - \frac{1}{{f'(4)}} = - 4\) , \( - 2\sqrt x \)
substituting into equation of line (for normal) M1
e.g. \(y - 2 = - 4(x - 4)\)
\(y = - 4x + 18\) AG N0
[4 marks]
recognition that \(y = 0\) at A (M1)
e.g. \( - 4x + 18 = 0\)
\(x = \frac{{18}}{4}\) \(\left( { = \frac{9}{2}} \right)\) A1 N2
[2 marks]
splitting into two appropriate parts (areas and/or integrals) (M1)
correct expression for area of R A2 N3
e.g. area of R = \(\int_0^4 {\sqrt x } {\rm{d}}x + \int_4^{4.5} {( - 4x + 18){\rm{d}}x} \) , \(\int_0^4 {\sqrt x } {\rm{d}}x + \frac{1}{2} \times 0.5 \times 2\) (triangle)
Note: Award A1 if dx is missing.
[3 marks]
correct expression for the volume from \(x = 0\) to \(x = 4\) (A1)
e.g. \(V = \int_0^4 {\pi \left[ {f{{(x)}^2}} \right]} {\rm{d}}x\) , \({\int_0^4 {\pi \sqrt x } ^2}{\rm{d}}x\) , \(\int_0^4 {\pi x{\rm{d}}x} \)
\(V = \left[ {\frac{1}{2}\pi {x^2}} \right]_0^4\) A1
\(V = \pi \left( {\frac{1}{2} \times 16 - \frac{1}{2} \times 0} \right)\) (A1)
\(V = 8\pi \) A1
finding the volume from \(x = 4\) to \(x = 4.5\)
EITHER
recognizing a cone (M1)
e.g. \(V = \frac{1}{3}\pi {r^2}h\)
\(V = \frac{1}{3}\pi {(2)^2} \times \frac{1}{2}\) (A1)
\( = \frac{{2\pi }}{3}\) A1
total volume is \(8\pi + \frac{2}{3}\pi \) \(\left( { = \frac{{26}}{3}\pi } \right)\) A1 N4
OR
\(V = \pi \int_4^{4.5} {{{( - 4x + 18)}^2}{\rm{d}}x} \) (M1)
\( = \int_4^{4.5} {\pi (16{x^2} - 144x + 324){\rm{d}}x} \)
\( = \pi \left[ {\frac{{16}}{3}{x^3} - 72{x^2} + 324x} \right]_4^{4.5}\) A1
\( = \frac{{2\pi }}{3}\) A1
total volume is \(8\pi + \frac{2}{3}\pi \) \(\left( { = \frac{{26}}{3}\pi } \right)\) A1 N4
[8 marks]
Examiners report
Parts (a) and (b) were well done by most candidates.
Parts (a) and (b) were well done by most candidates.
While quite a few candidates understood that both functions must be used to find the area in part (c), very few were actually able to write a correct expression for this area and this was due to candidates not knowing that they needed to integrate from \(0\) to \(4\) and then from \(4\) to \(4.5\).
On part (d), some candidates were able to earn follow through marks by setting up a volume expression, but most of these expressions were incorrect. If they did not get the expression for the area correct, there was little chance for them to get part (d) correct.
For those candidates who used their expression in part (c) for (d), there was a surprising amount of them who incorrectly applied distributive law of the exponent with respect to the addition or subtraction.

