| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = {x^2}\). The following diagram shows part of the graph of \(f\).
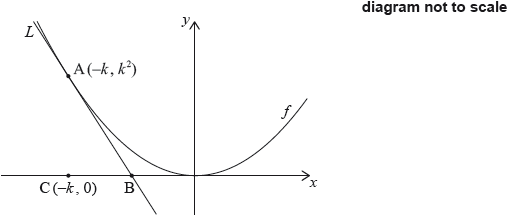
The line \(L\) is the tangent to the graph of \(f\) at the point \({\text{A}}( - k,{\text{ }}{k^2})\), and intersects the \(x\)-axis at point B. The point C is \(( - k,{\text{ }}0)\).
The region \(R\) is enclosed by \(L\), the graph of \(f\), and the \(x\)-axis. This is shown in the following diagram.
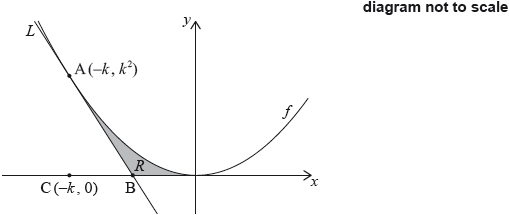
Write down \(f'(x)\).
Find the gradient of \(L\).
Show that the \(x\)-coordinate of B is \( - \frac{k}{2}\).
Find the area of triangle ABC, giving your answer in terms of \(k\).
Given that the area of triangle ABC is \(p\) times the area of \(R\), find the value of \(p\).
Markscheme
\(f'(x) = 2x\) A1 N1
[1 mark]
attempt to substitute \(x = - k\) into their derivative (M1)
gradient of \(L\) is \( - 2k\) A1 N2
[2 marks]
METHOD 1
attempt to substitute coordinates of A and their gradient into equation of a line (M1)
eg\(\,\,\,\,\,\)\({k^2} = - 2k( - k) + b\)
correct equation of \(L\) in any form (A1)
eg\(\,\,\,\,\,\)\(y - {k^2} = - 2k(x + k),{\text{ }}y = - 2kx - {k^2}\)
valid approach (M1)
eg\(\,\,\,\,\,\)\(y = 0\)
correct substitution into \(L\) equation A1
eg\(\,\,\,\,\,\)\( - {k^2} = - 2kx - 2{k^2},{\text{ }}0 = - 2kx - {k^2}\)
correct working A1
eg\(\,\,\,\,\,\)\(2kx = - {k^2}\)
\(x = - \frac{k}{2}\) AG N0
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{gradient}} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}},{\text{ }} - 2k = \frac{{{\text{rise}}}}{{{\text{run}}}}\)
recognizing \(y = 0\) at B (A1)
attempt to substitute coordinates of A and B into slope formula (M1)
eg\(\,\,\,\,\,\)\(\frac{{{k^2} - 0}}{{ - k - x}},{\text{ }}\frac{{ - {k^2}}}{{x + k}}\)
correct equation A1
eg\(\,\,\,\,\,\)\(\frac{{{k^2} - 0}}{{ - k - x}} = - 2k,{\text{ }}\frac{{ - {k^2}}}{{x + k}} = - 2k,{\text{ }} - {k^2} = - 2k(x + k)\)
correct working A1
eg\(\,\,\,\,\,\)\(2kx = - {k^2}\)
\(x = - \frac{k}{2}\) AG N0
[5 marks]
valid approach to find area of triangle (M1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}({k^2})\left( {\frac{k}{2}} \right)\)
area of \({\text{ABC}} = \frac{{{k^3}}}{4}\) A1 N2
[2 marks]
METHOD 1 (\(\int {f - {\text{triangle}}} \))
valid approach to find area from \( - k\) to 0 (M1)
eg\(\,\,\,\,\,\)\(\int_{ - k}^0 {{x^2}{\text{d}}x,{\text{ }}\int_0^{ - k} f } \)
correct integration (seen anywhere, even if M0 awarded) A1
eg\(\,\,\,\,\,\)\(\frac{{{x^3}}}{3},{\text{ }}\left[ {\frac{1}{3}{x^3}} \right]_{ - k}^0\)
substituting their limits into their integrated function and subtracting (M1)
eg\(\,\,\,\,\,\)\(0 - \frac{{{{( - k)}^3}}}{3}\), area from \( - k\) to 0 is \(\frac{{{k^3}}}{3}\)
Note: Award M0 for substituting into original or differentiated function.
attempt to find area of \(R\) (M1)
eg\(\,\,\,\,\,\)\(\int_{ - k}^0 {f(x){\text{d}}x - {\text{ triangle}}} \)
correct working for \(R\) (A1)
eg\(\,\,\,\,\,\)\(\frac{{{k^3}}}{3} - \frac{{{k^3}}}{4},{\text{ }}R = \frac{{{k^3}}}{{12}}\)
correct substitution into \({\text{triangle}} = pR\) (A1)
eg\(\,\,\,\,\,\)\(\frac{{{k^3}}}{4} = p\left( {\frac{{{k^3}}}{3} - \frac{{{k^3}}}{4}} \right),{\text{ }}\frac{{{k^3}}}{4} = p\left( {\frac{{{k^3}}}{{12}}} \right)\)
\(p = 3\) A1 N2
METHOD 2 (\(\int {(f - L)} \))
valid approach to find area of \(R\) (M1)
eg\(\,\,\,\,\,\)\(\int_{ - k}^{ - \frac{k}{2}} {{x^2} - ( - 2kx - {k^2}){\text{d}}x + \int_{ - \frac{k}{2}}^0 {{x^2}{\text{d}}x,{\text{ }}\int_{ - k}^{ - \frac{k}{2}} {(f - L) + \int_{ - \frac{k}{2}}^0 f } } } \)
correct integration (seen anywhere, even if M0 awarded) A2
eg\(\,\,\,\,\,\)\(\frac{{{x^3}}}{3} + k{x^2} + {k^2}x,{\text{ }}\left[ {\frac{{{x^3}}}{3} + k{x^2} + {k^2}x} \right]_{ - k}^{ - \frac{k}{2}} + \left[ {\frac{{{x^3}}}{3}} \right]_{ - \frac{k}{2}}^0\)
substituting their limits into their integrated function and subtracting (M1)
eg\(\,\,\,\,\,\)\(\left( {\frac{{{{\left( { - \frac{k}{2}} \right)}^3}}}{3} + k{{\left( { - \frac{k}{2}} \right)}^2} + {k^2}\left( { - \frac{k}{2}} \right)} \right) - \left( {\frac{{{{( - k)}^3}}}{3} + k{{( - k)}^2} + {k^2}( - k)} \right) + (0) - \left( {\frac{{{{\left( { - \frac{k}{2}} \right)}^3}}}{3}} \right)\)
Note: Award M0 for substituting into original or differentiated function.
correct working for \(R\) (A1)
eg\(\,\,\,\,\,\)\(\frac{{{k^3}}}{{24}} + \frac{{{k^3}}}{{24}},{\text{ }} - \frac{{{k^3}}}{{24}} + \frac{{{k^3}}}{4} - \frac{{{k^3}}}{2} + \frac{{{k^3}}}{3} - {k^3} + {k^3} + \frac{{{k^3}}}{{24}},{\text{ }}R = \frac{{{k^3}}}{{12}}\)
correct substitution into \({\text{triangle}} = pR\) (A1)
eg\(\,\,\,\,\,\)\(\frac{{{k^3}}}{4} = p\left( {\frac{{{k^3}}}{{24}} + \frac{{{k^3}}}{{24}}} \right),{\text{ }}\frac{{{k^3}}}{4} = p\left( {\frac{{{k^3}}}{{12}}} \right)\)
\(p = 3\) A1 N2
[7 marks]

