| Date | May 2016 | Marks available | 2 | Reference code | 16M.1.sl.TZ2.1 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The following diagram shows part of the graph of a quadratic function \(f\).
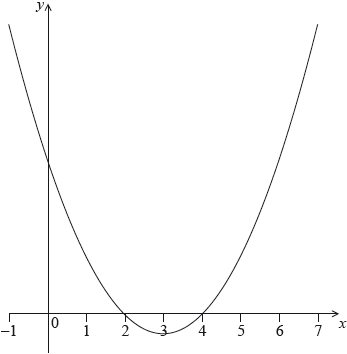
The vertex is at \((3,{\text{ }} - 1)\) and the \(x\)-intercepts at 2 and 4.
The function \(f\) can be written in the form \(f(x) = {(x - h)^2} + k\).
The function can also be written in the form \(f(x) = (x - a)(x - b)\).
Write down the value of \(h\) and of \(k\).
Write down the value of \(a\) and of \(b\).
Find the \(y\)-intercept.
Markscheme
\(h = 3,{\text{ }}k = - 1\) A1A1 N2
[2 marks]
\(a = 2,{\text{ }}b = 4{\text{ }}({\text{or }}a = 4,{\text{ }}b = 2)\) A1A1 N2
[2 marks]
attempt to substitute \(x = 0\) into their \(f\) (M1)
eg\(\,\,\,\,\,\)\({(0 - 3)^2} - 1,{\text{ }}(0 - 2)(0 - 4)\)
\(y = 8\) A1 N2
[2 marks]
Examiners report
Nearly all candidates performed well on this question, earning full marks on all three question parts.
Nearly all candidates performed well on this question, earning full marks on all three question parts. In part (b), there were some candidates who factored the quadratic expression correctly, but went on to give negative values for \(a\) and \(b\).
Nearly all candidates performed well on this question, earning full marks on all three question parts.

