| Date | May 2010 | Marks available | 2 | Reference code | 10M.2.sl.TZ2.10 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Sketch | Question number | 10 | Adapted from | N/A |
Question
Consider \(f(x) = x\ln (4 - {x^2})\) , for \( - 2 < x < 2\) . The graph of f is given below.
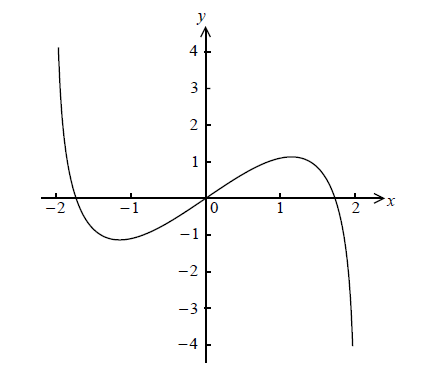
Let P and Q be points on the curve of f where the tangent to the graph of f is parallel to the x-axis.
(i) Find the x-coordinate of P and of Q.
(ii) Consider \(f(x) = k\) . Write down all values of k for which there are exactly two solutions.
Let \(g(x) = {x^3}\ln (4 - {x^2})\) , for \( - 2 < x < 2\) .
Show that \(g'(x) = \frac{{ - 2{x^4}}}{{4 - {x^2}}} + 3{x^2}\ln (4 - {x^2})\) .
Let \(g(x) = {x^3}\ln (4 - {x^2})\) , for \( - 2 < x < 2\) .
Sketch the graph of \(g'\) .
Let \(g(x) = {x^3}\ln (4 - {x^2})\) , for \( - 2 < x < 2\) .
Consider \(g'(x) = w\) . Write down all values of w for which there are exactly two solutions.
Markscheme
(i) \( - 1.15{\text{, }}1.15\) A1A1 N2
(ii) recognizing that it occurs at P and Q (M1)
e.g. \(x = - 1.15\) , \(x = 1.15\)
\(k = - 1.13\) , \(k = 1.13\) A1A1 N3
[5 marks]
evidence of choosing the product rule (M1)
e.g. \(uv' + vu'\)
derivative of \({x^3}\) is \(3{x^2}\) (A1)
derivative of \(\ln (4 - {x^2})\) is \(\frac{{ - 2x}}{{4 - {x^2}}}\) (A1)
correct substitution A1
e.g. \({x^3} \times \frac{{ - 2x}}{{4 - {x^2}}} + \ln (4 - {x^2}) \times 3{x^2}\)
\(g'(x) = \frac{{ - 2{x^4}}}{{4 - {x^2}}} + 3{x^2}\ln (4 - {x^2})\) AG N0
[4 marks]
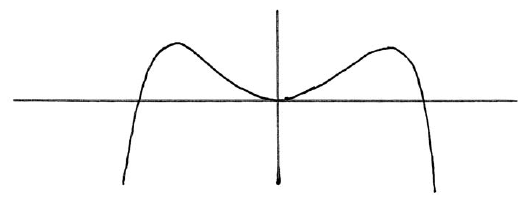 A1A1 N2
A1A1 N2
[2 marks]
\(w = 2.69\) , \(w < 0\) A1A2 N2
[3 marks]
Examiners report
Many candidates correctly found the x-coordinates of P and Q in (a)(i) with their GDC. In (a)(ii) some candidates incorrectly interpreted the words “exactly two solutions” as an indication that the discriminant of a quadratic was required. Many failed to realise that the values of k they were looking for in this question were the y-coordinates of the points found in (a)(i).
Many candidates were unclear in their application of the product formula in the verifying the given derivative of g. Showing that the derivative was the given expression often received full marks though it was not easy to tell in some cases if that demonstration came through understanding of the product and chain rules or from reasoning backwards from the given result.
Some candidates drew their graphs of the derivative in (c) on their examination papers despite clear instructions to do their work on separate sheets. Most who tried to plot the graph in (c) did so successfully.
Correct solutions to 10(d) were not often seen.

