| Date | November 2011 | Marks available | 3 | Reference code | 11N.2.sl.TZ0.10 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{20x}}{{{{\rm{e}}^{0.3x}}}}\) , for \(0 \le x \le 20\) .
Sketch the graph of f .
(i) Write down the x-coordinate of the maximum point on the graph of f .
(ii) Write down the interval where f is increasing.
Show that \(f'(x) = \frac{{20 - 6x}}{{{{\rm{e}}^{0.3x}}}}\) .
Find the interval where the rate of change of f is increasing.
Markscheme
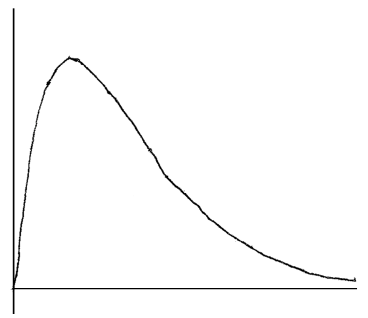 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for approximately correct shape with inflexion/change of curvature, A1 for maximum skewed to the left, A1 for asymptotic behaviour to the right.
[3 marks]
(i) \(x = 3.33\) A1 N1
(ii) correct interval, with right end point \(3\frac{1}{3}\) A1A1 N2
e.g. \(0 < x \le 3.33\) , \(0 \le x < 3\frac{1}{3}\)
Note: Accept any inequalities in the right direction.
[3 marks]
valid approach (M1)
e.g. quotient rule, product rule
2 correct derivatives (must be seen in product or quotient rule) (A1)(A1)
e.g. \(20\) , \(0.3{{\rm{e}}^{0.3x}}\) or \( - 0.3{{\rm{e}}^{ - 0.3x}}\)
correct substitution into product or quotient rule A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} - 20x(0.3){{\rm{e}}^{0.3x}}}}{{{{({{\rm{e}}^{0.3x}})}^2}}}\) , \(20{{\rm{e}}^{ - 0.3x}} + 20x( - 0.3){{\rm{e}}^{ - 0.3x}}\)
correct working A1
e.g. \(\frac{{20{{\rm{e}}^{0.3x}} - 6x{{\rm{e}}^{0.3x}}}}{{{{\rm{e}}^{0.6x}}}}\) , \(\frac{{{{\rm{e}}^{0.3x}}(20 - 20x(0.3))}}{{{{{\rm{(}}{{\rm{e}}^{0.3x}})}^2}}}\) , \({{\rm{e}}^{ - 0.3x}}(20 + 20x( - 0.3))\)
\(f'(x) = \frac{{20 - 6x}}{{{{\rm{e}}^{0.3x}}}}\) AG N0
[5 marks]
consideration of \(f'\) or \(f''\) (M1)
valid reasoning R1
e.g. sketch of \(f'\) , \(f''\) is positive, \(f'' = 0\) , reference to minimum of \(f'\)
correct value \(6.6666666 \ldots \) \(\left( {6\frac{2}{3}} \right)\) (A1)
correct interval, with both endpoints A1 N3
e.g. \(6.67 < x \le 20\) , \(6\frac{2}{3} \le x < 20\)
[4 marks]
Examiners report
Many candidates earned the first four marks of the question in parts (a) and (b) for correctly using their GDC to graph and find the maximum value.
Many candidates earned the first four marks of the question in parts (a) and (b) for correctly using their GDC to graph and find the maximum value.
Most had a valid approach in part (c) using either the quotient or product rule, but many had difficulty applying the chain rule with a function involving e and simplifying.
Part (d) was difficult for most candidates. Although many associated rate of change with derivative, only the best-prepared students had valid reasoning and could find the correct interval with both endpoints.

