| Date | May 2012 | Marks available | 6 | Reference code | 12M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{x}{{ - 2{x^2} + 5x - 2}}\) for \( - 2 \le x \le 4\) , \(x \ne \frac{1}{2}\) , \(x \ne 2\) . The graph of \(f\) is given below.
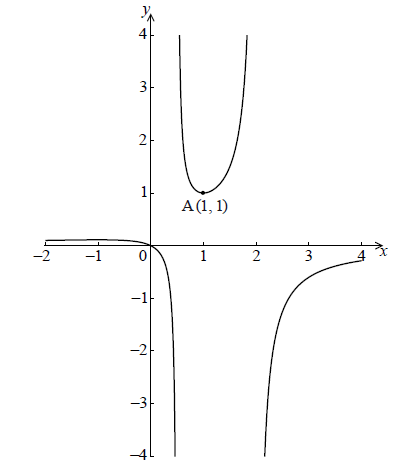
The graph of \(f\) has a local minimum at A(\(1\), \(1\)) and a local maximum at B.
Use the quotient rule to show that \(f'(x) = \frac{{2{x^2} - 2}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\) .
Hence find the coordinates of B.
Given that the line \(y = k\) does not meet the graph of f , find the possible values of k .
Markscheme
correct derivatives applied in quotient rule (A1)A1A1
\(1\), \( - 4x + 5\)
Note: Award (A1) for 1, A1 for \( - 4x\) and A1 for \(5\), only if it is clear candidates are using the quotient rule.
correct substitution into quotient rule A1
e.g. \(\frac{{1 \times ( - 2{x^2} + 5x - 2) - x( - 4x + 5)}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\) , \(\frac{{ - 2{x^2} + 5x - 2 - x( - 4x + 5)}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\)
correct working (A1)
e.g. \(\frac{{ - 2{x^2} + 5x - 2 - ( - 4{x^2} + 5x)}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\)
expression clearly leading to the answer A1
e.g. \(\frac{{ - 2{x^2} + 5x - 2 + 4{x^2} - 5x}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\)
\(f'(x) = \frac{{2{x^2} - 2}}{{{{( - 2{x^2} + 5x - 2)}^2}}}\) AG N0
[6 marks]
evidence of attempting to solve \(f'(x) = 0\) (M1)
e.g. \(2{x^2} - 2 = 0\)
evidence of correct working A1
e.g. \({x^2} = 1,\frac{{ \pm \sqrt {16} }}{4}{\text{, }}2(x - 1)(x + 1)\)
correct solution to quadratic (A1)
e.g. \(x = \pm 1\)
correct x-coordinate \(x = - 1\) (may be seen in coordinate form \(\left( { - 1,\frac{1}{9}} \right)\) ) A1 N2
attempt to substitute \( - 1\) into f (do not accept any other value) (M1)
e.g. \(f( - 1) = \frac{{ - 1}}{{ - 2 \times {{( - 1)}^2} + 5 \times ( - 1) - 2}}\)
correct working
e.g. \(\frac{{ - 1}}{{ - 2 - 5 - 2}}\) A1
correct y-coordinate \(y = \frac{1}{9}\) (may be seen in coordinate form \(\left( { - 1,\frac{1}{9}} \right)\) ) A1 N2
[7 marks]
recognizing values between max and min (R1)
\(\frac{1}{9} < k < 1\) A2 N3
[3 marks]
Examiners report
While most candidates answered part (a) correctly, there were some who did not show quite enough work for a "show that" question. A very small number of candidates did not follow the instruction to use the quotient rule.
In part (b), most candidates knew that they needed to solve the equation \(f'(x) = 0\) , and many were successful in answering this question correctly. However, some candidates failed to find both values of x, or made other algebraic errors in their solutions. One common error was to find only one solution for \({x^2} = 1\) ; another was to work with the denominator equal to zero, rather than the numerator.
In part (c), a significant number of candidates seemed to think that the line \(y = k\) was a vertical line, and attempted to find the vertical asymptotes. Others tried looking for a horizontal asymptote. Fortunately, there were still a good number of intuitive candidates who recognized the link with the graph and with part (b), and realized that the horizontal line must pass through the space between the given local minimum and the local maximum they had found in part (b).

