| Date | May 2010 | Marks available | 1 | Reference code | 10M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = 6 + 6\sin x\) . Part of the graph of f is shown below.
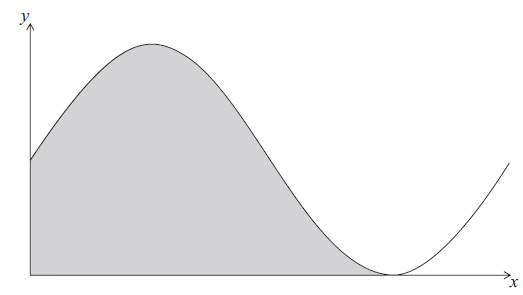
The shaded region is enclosed by the curve of f , the x-axis, and the y-axis.
Solve for \(0 \le x < 2\pi \)
(i) \(6 + 6\sin x = 6\) ;
(ii) \(6 + 6\sin x = 0\) .
Write down the exact value of the x-intercept of f , for \(0 \le x < 2\pi \) .
The area of the shaded region is k . Find the value of k , giving your answer in terms of \(\pi \) .
Let \(g(x) = 6 + 6\sin \left( {x - \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Give a full geometric description of this transformation.
Let \(g(x) = 6 + 6\sin \left( {x - \frac{\pi }{2}} \right)\) . The graph of f is transformed to the graph of g.
Given that \(\int_p^{p + \frac{{3\pi }}{2}} {g(x){\rm{d}}x} = k\) and \(0 \le p < 2\pi \) , write down the two values of p.
Markscheme
(i) \(\sin x = 0\) A1
\(x = 0\) , \(x = \pi \) A1A1 N2
(ii) \(\sin x = - 1\) A1
\(x = \frac{{3\pi }}{2}\) A1 N1
[5 marks]
\(\frac{{3\pi }}{2}\) A1 N1
[1 mark]
evidence of using anti-differentiation (M1)
e.g. \(\int_0^{\frac{{3\pi }}{2}} {(6 + 6\sin x){\rm{d}}x} \)
correct integral \(6x - 6\cos x\) (seen anywhere) A1A1
correct substitution (A1)
e.g. \(6\left( {\frac{{3\pi }}{2}} \right) - 6\cos \left( {\frac{{3\pi }}{2}} \right) - ( - 6\cos 0)\) , \(9\pi - 0 + 6\)
\(k = 9\pi + 6\) A1A1 N3
[6 marks]
translation of \(\left( {\begin{array}{*{20}{c}}
{\frac{\pi }{2}}\\
0
\end{array}} \right)\) A1A1 N2
[2 marks]
recognizing that the area under g is the same as the shaded region in f (M1)
\(p = \frac{\pi }{2}\) , \(p = 0\) A1A1 N3
[3 marks]
Examiners report
Many candidates again had difficulty finding the common angles in the trigonometric equations. In part (a), some did not show sufficient working in solving the equations. Others obtained a single solution in (a)(i) and did not find another. Some candidates worked in degrees; the majority worked in radians.
While some candidates appeared to use their understanding of the graph of the original function to find the x-intercept in part (b), most used their working from part (a)(ii) sometimes with follow-through on an incorrect answer.
Most candidates recognized the need for integration in part (c) but far fewer were able to see the solution through correctly to the end. Some did not show the full substitution of the limits, having incorrectly assumed that evaluating the integral at 0 would be 0; without this working, the mark for evaluating at the limits could not be earned. Again, many candidates had trouble working with the common trigonometric values.
While there was an issue in the wording of the question with the given domains, this did not appear to bother candidates in part (d). This part was often well completed with candidates using a variety of language to describe the horizontal translation to the right by \(\frac{\pi }{2}\) .
Most candidates who attempted part (e) realized that the integral was equal to the value that they had found in part (c), but a majority tried to integrate the function g without success. Some candidates used sketches to find one or both values for p. The problem in the wording of the question did not appear to have been noticed by candidates in this part either.

