| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.sl.TZ1.9 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 9 | Adapted from | N/A |
Question
A particle P moves along a straight line so that its velocity, \(v\,{\text{m}}{{\text{s}}^{ - 1}}\), after \(t\) seconds, is given by \(v = \cos 3t - 2\sin t - 0.5\), for \(0 \leqslant t \leqslant 5\). The initial displacement of P from a fixed point O is 4 metres.
The following sketch shows the graph of \(v\).
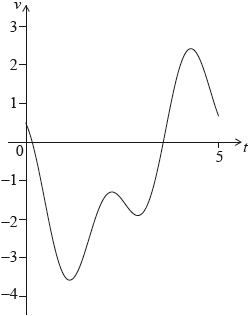
Find the displacement of P from O after 5 seconds.
Find when P is first at rest.
Write down the number of times P changes direction.
Find the acceleration of P after 3 seconds.
Find the maximum speed of P.
Markscheme
METHOD 1
recognizing \(s = \int v \) (M1)
recognizing displacement of P in first 5 seconds (seen anywhere) A1
(accept missing \({\text{d}}t\))
eg\(\,\,\,\,\,\)\(\int_0^5 {v{\text{d}}t,{\text{ }} - 3.71591} \)
valid approach to find total displacement (M1)
eg\(\,\,\,\,\,\)\(4 + ( - 3.7159),{\text{ }}s = 4 + \int_0^5 v \)
0.284086
0.284 (m) A2 N3
METHOD 2
recognizing \(s = \int v \) (M1)
correct integration A1
eg\(\,\,\,\,\,\)\(\frac{1}{3}\sin 3t + 2\cos t - \frac{t}{2} + c\) (do not penalize missing “\(c\)”)
attempt to find \(c\) (M1)
eg\(\,\,\,\,\,\)\(4 = \frac{1}{3}\sin (0) + 2\cos (0)--\frac{0}{2} + c,{\text{ }}4 = \frac{1}{3}\sin 3t + 2\cos t - \frac{t}{2} + c,{\text{ }}2 + c = 4\)
attempt to substitute \(t = 5\) into their expression with \(c\) (M1)
eg\(\,\,\,\,\,\)\(s(5),{\text{ }}\frac{1}{3}\sin (15) + 2\cos (5)5--\frac{5}{2} + 2\)
0.284086
0.284 (m) A1 N3
[5 marks]
recognizing that at rest, \(v = 0\) (M1)
\(t = 0.179900\)
\(t = 0.180{\text{ (secs)}}\) A1 N2
[2 marks]
recognizing when change of direction occurs (M1)
eg\(\,\,\,\,\,\)\(v\) crosses \(t\) axis
2 (times) A1 N2
[2 marks]
acceleration is \({v'}\) (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(v'(3)\)
0.743631
\(0.744{\text{ }}({\text{m}}{{\text{s}}^{ - 2}})\) A1 N2
[2 marks]
valid approach involving max or min of \(v\) (M1)
eg\(\,\,\,\,\,\)\(v\prime = 0,{\text{ }}a = 0\), graph
one correct co-ordinate for min (A1)
eg\(\,\,\,\,\,\)\(1.14102,{\text{ }}-3.27876\)
\(3.28{\text{ }}({\text{m}}{{\text{s}}^{ - 1}})\) A1 N2
[3 marks]
Examiners report
This question was not well done throughout. Analytical approaches were almost always unsuccessful as a result of poor integration and differentiation skills and many of the errors were a result of having the GDC in degree mode. In (a), most candidates recognized the need to integrate \(v\) to find the displacement, although a significant number differentiated \(v\). Of those that integrated, many assumed incorrectly that the initial displacement was the value of the constant of integration. Some candidates integrated \(\left| v \right|\) and obtained no marks for an invalid approach. In the case where a correct definite integral was given, it was disappointing to see many candidates try to evaluate it analytically rather than using their GDC.
This question was not well done throughout. Analytical approaches were almost always unsuccessful as a result of poor integration and differentiation skills and many of the errors were a result of having the GDC in degree mode. In part (b), many candidates did not read the question carefully and gave the two occasions, in the given domain, where the particle was at rest.
This question was not well done throughout. Analytical approaches were almost always unsuccessful as a result of poor integration and differentiation skills and many of the errors were a result of having the GDC in degree mode. In part (c), many candidates did not appreciate that velocity is a vector and that the particle would change direction when its velocity changes sign. Consequently, many candidates gave the incorrect answer of four changes in directions, rather than the correct two direction changes.
This question was not well done throughout. Analytical approaches were almost always unsuccessful as a result of poor integration and differentiation skills and many of the errors were a result of having the GDC in degree mode. Part (d), was done very poorly, with candidates struggling to differentiate sine and cosine correctly and to evaluate their derivative. As with question 3, many candidates worked with the incorrect angle setting on their calculator.
This question was not well done throughout. Analytical approaches were almost always unsuccessful as a result of poor integration and differentiation skills and many of the errors were a result of having the GDC in degree mode. Few candidates attempted part (e). Of those that did, many attempted to find the largest local maximum of the graph rather than least local minimum as they did not recognise speed as \(\left| v \right|\).

