| Date | None Specimen | Marks available | 7 | Reference code | SPNone.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch and Write down | Question number | 9 | Adapted from | N/A |
Question
Let \(h(x) = \frac{{2x - 1}}{{x + 1}}\) , \(x \ne - 1\) .
Find \({h^{ - 1}}(x)\) .
(i) Sketch the graph of h for \( - 4 \le x \le 4\) and \( - 5 \le y \le 8\) , including any asymptotes.
(ii) Write down the equations of the asymptotes.
(iii) Write down the x-intercept of the graph of h .
Let R be the region in the first quadrant enclosed by the graph of h , the x-axis and the line \(x = 3\).
(i) Find the area of R.
(ii) Write down an expression for the volume obtained when R is revolved through \({360^ \circ }\) about the x-axis.
Markscheme
\(y = \frac{{2x - 1}}{{x + 1}}\)
interchanging x and y (seen anywhere) M1
e.g. \(x = \frac{{2y - 1}}{{y + 1}}\)
correct working A1
e.g. \(xy + x = 2y - 1\)
collecting terms A1
e.g. \(x + 1 = 2y - xy\) , \(x + 1 = y(2 - x)\)
\({h^{ - 1}}(x) = \frac{{x + 1}}{{2 - x}}\) A1 N2
[4 marks]
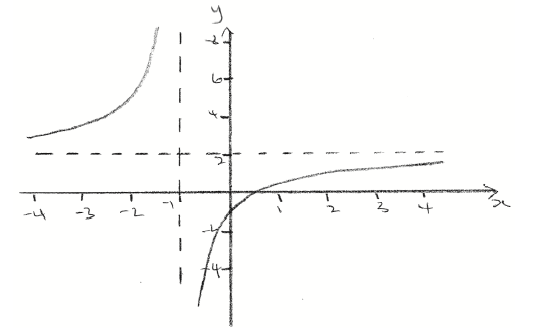 A1A1A1A1 N4
A1A1A1A1 N4
Note: Award A1 for approximately correct intercepts, A1 for correct shape, A1 for asymptotes, A1 for approximately correct domain and range.
(ii) \(x = - 1\) , \(y = 2\) A1A1 N2
(iii) \(\frac{1}{2}\) A1 N1
[7 marks]
(i) \({\text{area}} = 2.06\) A2 N2
(ii) attempt to substitute into volume formula (do not accept \(\pi \int_a^b {{y^2}{\rm{d}}x} \) ) M1
volume \( = \pi {\int_{\frac{1}{2}}^3 {\left( {\frac{{2x - 1}}{{x + 1}}} \right)} ^2}{\rm{d}}x\) A2 N3
[5 marks]

