| Date | November 2012 | Marks available | 2 | Reference code | 12N.2.sl.TZ0.5 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 5 | Adapted from | N/A |
Question
Let \(f(x) = a\cos (b(x - c))\) . The diagram below shows part of the graph of f , for \(0 \le x \le 10\) .
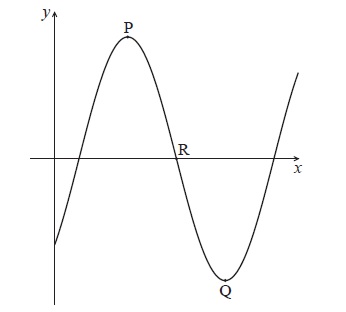
The graph has a local maximum at P(3, 5) , a local minimum at Q(7, − 5) , and crosses the x-axis at R.
Write down the value of
(i) \(a\) ;
(ii) \(c\) .
Find the value of b .
Find the x-coordinate of R.
Markscheme
(i) \(a = 5\) (accept \( - 5\) ) A1 N1
(ii) \(c = 3\) (accept \(c = 7\) , if \(a = - 5\) ) A1 N1
Note: Accept other correct values of c, such as 11, \( - 5\), etc.
[2 marks]
attempt to find period (M1)
e.g. 8 , \(b = \frac{{2\pi }}{{{\rm{period}}}}\)
\(0.785398 \ldots \)
\(b = \frac{{2\pi }}{8}\) (exact), \(\frac{\pi }{4}\) , 0.785 [\(0.785{\text{, }}0.786\)] (do not accept 45) A1 N2
[2 marks]
valid approach (M1)
e.g. \(f(x) = 0\) , symmetry of curve
\(x = 5\) (accept \((5{\text{ ,}}0))\) A1 N2
[2 marks]
Examiners report
Part (a) (i) was well answered in general. There were more difficulties in finding the correct value of the parameter c.
Finding the correct value of b in part (b) also proved difficult as many did not realize the period was equal to 8.
Most candidates could handle part (c) without difficulties using their GDC or working with the symmetry of the curve although follow through from errors in part (b) was often not awarded because candidates failed to show any working by writing down the equations they entered into their GDC.

