| Date | November 2012 | Marks available | 3 | Reference code | 12N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = {x^3} - 2x - 4\) . The following diagram shows part of the curve of f .
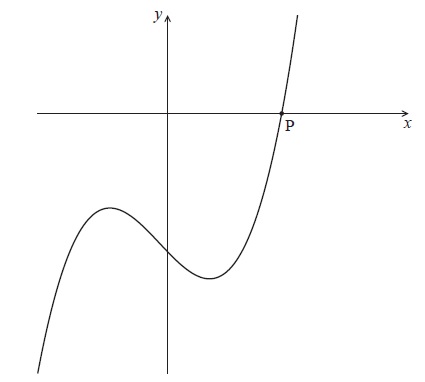
The curve crosses the x-axis at the point P.
Write down the x-coordinate of P.
Write down the gradient of the curve at P.
Find the equation of the normal to the curve at P, giving your equation in the form \(y = ax + b\) .
Markscheme
\(x = 2\) (accept \((2{\text{, }}0)\)) A1 N1
[1 mark]
evidence of finding gradient of f at \(x = 2\) (M1)
e.g. \(f'(2)\)
the gradient is 10 A1 N2
[2 marks]
evidence of negative reciprocal of gradient (M1)
e.g. \(\frac{{ - 1}}{{f'(x)}}\) , \( - \frac{1}{{10}}\)
evidence of correct substitution into equation of a line (A1)
e.g. \(y - 0 = \frac{{ - 1}}{{10}}(x - 2)\) , \(0 = - 0.1(2) + b\)
\(y = - \frac{1}{{10}}x + \frac{2}{{10}}\) (accept \(a = - 0.1\) , \(b = 0.2\) ) A1 N2
[3 marks]
Examiners report
This question was generally done well.
Most candidates did not use their GDC in part (b), resulting in a variety of careless errors occasionally arising either in differentiating or substituting.
There were some candidates who did not know the relationship between gradients of perpendicular lines while others found the equation of the tangent rather than the normal in part (c).

