| Date | May 2010 | Marks available | 2 | Reference code | 10M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
Let \(f(x) = {{\rm{e}}^x}\sin 2x + 10\) , for \(0 \le x \le 4\) . Part of the graph of f is given below.
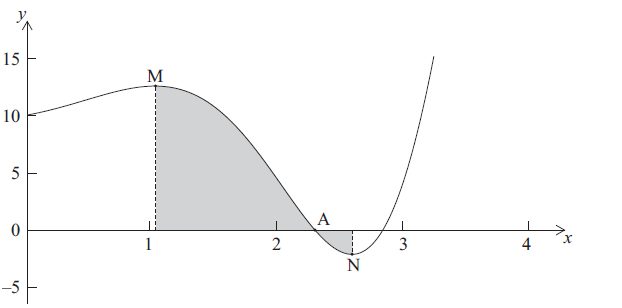
There is an x-intercept at the point A, a local maximum point at M, where \(x = p\) and a local minimum point at N, where \(x = q\) .
Write down the x-coordinate of A.
Find the value of
(i) p ;
(ii) q .
Find \(\int_p^q {f(x){\rm{d}}x} \) . Explain why this is not the area of the shaded region.
Markscheme
\(2.31\) A1 N1
[1 mark]
(i) 1.02 A1 N1
(ii) 2.59 A1 N1
[2 marks]
\(\int_p^q {f(x){\rm{d}}x} = 9.96\) A1 N1
split into two regions, make the area below the x-axis positive R1R1 N2
[3 marks]
Examiners report
Parts (a) and (b) were generally well answered, the main problem being the accuracy.
Parts (a) and (b) were generally well answered, the main problem being the accuracy.
Many students lacked the calculator skills to successfully complete (6)(c) in that they could not find the value of the definite integral. Some tried to find it by hand. When trying to explain why the integral was not the area, most knew the region under the x-axis was the cause of the integral not giving the total area, but the explanations were not sufficiently clear. It was often stated that the area below the axis was negative rather than the integral was negative.

