| Date | November 2017 | Marks available | 3 | Reference code | 17N.2.sl.TZ0.2 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 2 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{6{x^2} - 4}}{{{{\text{e}}^x}}}\), for \(0 \leqslant x \leqslant 7\).
Find the \(x\)-intercept of the graph of \(f\).
The graph of \(f\) has a maximum at the point A. Write down the coordinates of A.
On the following grid, sketch the graph of \(f\).
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0,{\text{ }} \pm 0.816\)
0.816496
\(x = \sqrt {\frac{2}{3}} \) (exact), 0.816 A1 N2
[2 marks]
\((2.29099,{\text{ }}2.78124)\)
\({\text{A}}(2.29,{\text{ }}2.78)\) A1A1 N2
[2 marks]
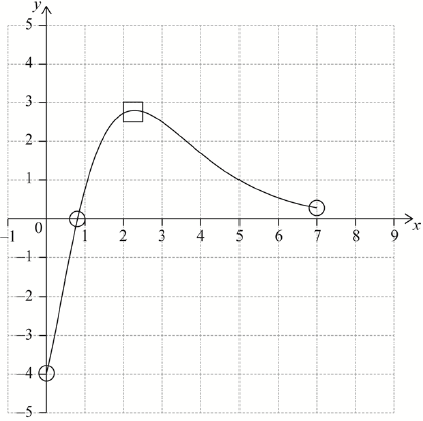A1A1A1 N3
Notes: Award A1 for correct domain and endpoints at \(x = 0\) and \(x = 7\) in circles,
A1 for maximum in square,
A1 for approximately correct shape that passes through their \(x\)-intercept in circle and has changed from concave down to concave up between 2.29 and 7.
[3 marks]
