| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.sl.TZ0.3 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = 2\ln (x - 3)\), for \(x > 3\). The following diagram shows part of the graph of \(f\).
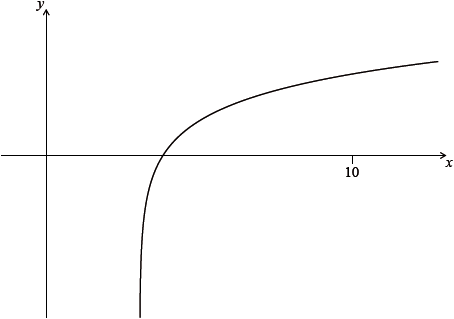
Find the equation of the vertical asymptote to the graph of \(f\).
Find the \(x\)-intercept of the graph of \(f\).
The region enclosed by the graph of \(f\), the \(x\)-axis and the line \(x = 10\) is rotated \(360\)° about the \(x\)-axis. Find the volume of the solid formed.
Markscheme
valid approach (M1)
eg\(\;\;\;\)horizontal translation \(3\) units to the right
\(x = 3\) (must be an equation) A1 N2
[2 marks]
valid approach (M1)
eg\(\;\;\;f(x) = 0,{\text{ }}{e^0} = x - 3\)
\(4,{\text{ }}x = 4,{\text{ }}(4,{\text{ }}0)\) A1 N2
[2 marks]
attempt to substitute either their correct limits or the function into formula involving \({f^2}\) (M1)
eg\(\;\;\;\int_4^{10} {{f^2},{\text{ }}\pi \int {{{\left( {2\ln (x - 3)} \right)}^2}{\text{d}}x} } \)
\(141.537\)
volume = \(142\) A2 N3
[3 marks]
Total [7 marks]

