| Date | November 2010 | Marks available | 4 | Reference code | 10N.2.sl.TZ0.8 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = x\ln (4 - {x^2})\) , for \( - 2 < x < 2\) . The graph of f is shown below.
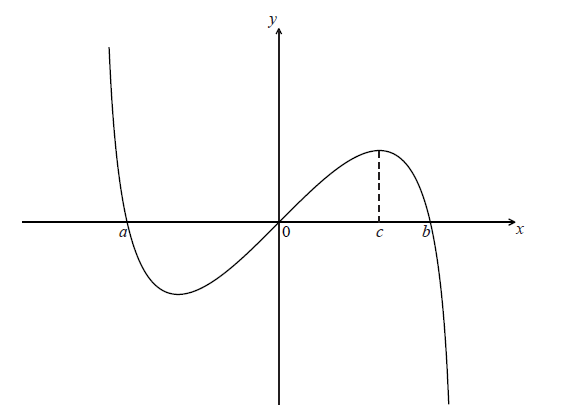
The graph of f crosses the x-axis at \(x = a\) , \(x = 0\) and \(x = b\) .
Find the value of a and of b .
The graph of f has a maximum value when \(x = c\) .
Find the value of c .
The region under the graph of f from \(x = 0\) to \(x = c\) is rotated \({360^ \circ }\) about the x-axis. Find the volume of the solid formed.
Let R be the region enclosed by the curve, the x-axis and the line \(x = c\) , between \(x = a\) and \(x = c\) .
Find the area of R .
Markscheme
evidence of valid approach (M1)
e.g. \(f(x) = 0\) , graph
\(a = - 1.73\) , \(b = 1.73\) \((a = - \sqrt 3 {\text{, }}b = \sqrt 3 )\) A1A1 N3
[3 marks]
attempt to find max (M1)
e.g. setting \(f'(x) = 0\) , graph
\(c = 1.15\) (accept (1.15, 1.13)) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula M1
e.g. \(V = \pi {\int_0^c {\left[ {f(x)} \right]} ^2}{\rm{d}}x\) , \(\pi {\int {\left[ {x\ln (4 - {x^2})} \right]} ^2}\) , \(\pi \int_0^{1.149 \ldots } {{y^2}{\rm{d}}x} \)
\(V = 2.16\) A2 N2
[3 marks]
valid approach recognizing 2 regions (M1)
e.g. finding 2 areas
correct working (A1)
e.g. \(\int_0^{ - 1.73 \ldots } {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \) , \( - \int_{ - 1.73 \ldots }^0 {f(x){\rm{d}}x + } \int_0^{1.149 \ldots } {f(x){\rm{d}}x} \)
area \( = 2.07\) (accept 2.06) A2 N3
[4 marks]
Examiners report
This question was well done by many candidates. If there were problems, it was often with incorrect or inappropriate GDC use. For example, some candidates used the trace feature to answer parts (a) and (b), which at best, only provides an approximation.
This question was well done by many candidates. If there were problems, it was often with incorrect or inappropriate GDC use. For example, some candidates used the trace feature to answer parts (a) and (b), which at best, only provides an approximation.
Most candidates were able to set up correct expressions for parts (c) and (d) and if they had used their calculators, could find the correct answers. Some candidates omitted the important parts of the volume formula. Analytical approaches to (c) and (d) were always futile and no marks were gained.
Most candidates were able to set up correct expressions for parts (c) and (d) and if they had used their calculators, could find the correct answers. Some candidates omitted the important parts of the volume formula. Analytical approaches to (c) and (d) were always futile and no marks were gained.

