5.10.2 Analytical Solutions to Differential Equations

Separation of Variables

What is separation of variables?

Separation of variables can be used to solve certain types of first order differential equations
Look out for equations of the form $\frac{d y}{d x} = g (x) h (y)$

i.e. $\frac{d y}{d x}$ is a function of $x$ multiplied by a function of $y$
be careful – the ‘function of $x$ ’ $g (x)$ may just be a constant!

For example in $\frac{d y}{d x} = 6 y$ , $g (x) = 6$ and $h (y) = y$

If the equation is in that form you can use separation of variables to try to solve it
If the equation is not in that form you will need to use another solution method

How do I solve a differential equation using separation of variables?

STEP 1: Rearrange the equation into the form $(\frac{1}{h (y)}) \frac{d y}{d x} = g (x)$
STEP 2: Take the integral of both sides to change the equation into the form

$\int_{}^{} \frac{1}{h (y)} d y = \int_{}^{} g (x) d x$

- You can think of this step as ‘multiplying the $d x$ across and integrating both sides’
  - Mathematically that’s not quite what is actually happening, but it will get you the right answer here!
STEP 3: Work out the integrals on both sides of the equation to find the general solution to the differential equation
- Don’t forget to include a constant of integration
  - Although there are two integrals, you only need to include one constant of integration
- Look out for integrals that require you to use partial fractions to solve them
  - See ‘Integrating with Partial Fractions’ in 5.9 Advanced Integration
STEP 4: Use any boundary or initial conditions in the question to work out the value of the integration constant
STEP 5: If necessary, rearrange the solution into the form required by the question

Exam Tip

Be careful with letters – the equation on an exam may not use $x$ and $y$ as the variables
Unless the question asks for it, you don’t have to change your solution into $y = f (x)$ form – sometimes it might be more convenient to leave your solution in another form

Worked Example

For each of the following differential equations, either (i) solve the equation by using separation of variables giving your answer in the form $y = f (x)$ , or (ii) state why the equation may not be solved using separation of variables.

a) $\frac{d y}{d x} = \frac{e^{x} + 4 x}{3 y^{2}}$ .

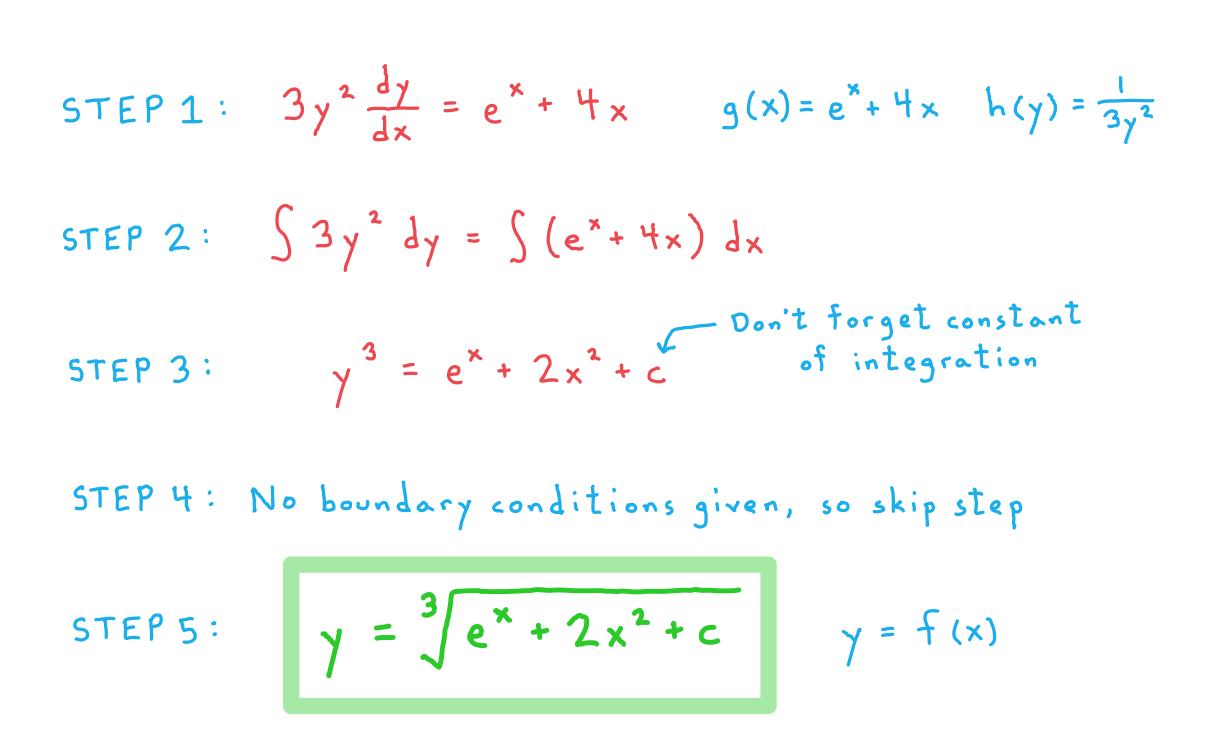
5-10-2-ib-aa-hl-separation-of-variables-a-we-solution

b) $\frac{d y}{d x} = 4 x y - 2 \ln x$ .

5-10-2-ib-aa-hl-separation-of-variables-b-we-solution

c) $\frac{d y}{d x} = 2 y^{2} + 2 y$ , given that $y = 2$ when $x = 0$ .

5-10-2-ib-aa-hl-separation-of-variables-c-we-solution

Homogeneous Differential Equations

What is a homogeneous first order differential equation?

If a first order differential equation can be written in the form $\frac{d y}{d x} = f (\frac{y}{x})$ then it is said to be homogeneous

How do I solve a homogeneous first order differential equation?

These equations can be solved using the substitution $v = \frac{y}{x} \Leftrightarrow y = v x$
STEP 1: If necessary, rearrange the equation into the form $\frac{d y}{d x} = f (\frac{y}{x})$
STEP 2: Replace all instances of $\frac{y}{x}$ in your equation with v
STEP 3: Use the product rule and implicit differentiation to replace $\frac{d y}{d x}$ in your equation with $v + x \frac{d v}{d x}$

This is because $y = v x ⟹ \frac{d y}{d x} = \frac{d}{d x} (v x) = v \frac{d}{d x} (x) + x \frac{d}{d x} (v) = v + x \frac{d v}{d x}$

STEP 4: Solve your new differential equation to find the solution in terms of v and x

You may need to use other methods for differential equations, such as separation of variables, at this stage

STEP 5: Substitute $v = \frac{y}{x}$ into the solution from Step 4, in order to find the solution in terms of y and x

What else should I know about solving homogeneous first order differential equations?

After finding the solution in terms of y and x you may be asked to do other things with the solution

For example you may be asked to find the solution corresponding to certain initial or boundary conditions
Or you may be asked to express your answer in a particular form, such as y = f(x)

It is sometimes possible to solve differential equations that are not homogeneous by using the substitution $v = \frac{y}{x}$

For such a situation in an exam question, you would be told explicitly to use the substitution
You would not be expected to know that you could use the substitution in a case where the differential equation was not homogeneous

Exam Tip

Unless the question asks for it, you don’t have to change your solution into y = f(x) form – sometimes it might be more convenient to leave your solution in another form

Worked Example

Consider the differential equation $x y \frac{d y}{d x} = y^{2} - x^{2}$ where y = 3 when x = 1.

Show that the differential equation is homogeneous.

5-10-2-ib-aa-hl-homogeneous-diff-eqn-a-we-solution

Use the substitution

v = \frac{y}{x}

to solve the differential equation with the given boundary condition.

5-10-2-ib-aa-hl-homogeneous-diff-eqn-b-we-solution

Integrating Factor

What is an integrating factor?

An integrating factor can be used to solve a differential equation that can be written in the standard form $\frac{d y}{d x} + p (x) y = q (x)$

Be careful – the ‘functions of x’ p(x) and q(x) may just be constants!

For example in $\frac{d y}{d x} + 6 y = e^{- 2 x}$ , p(x) = 6 and q(x) = e^-2x
While in $\frac{d y}{d x} + \frac{y}{2 x} = 12$ , $p (x) = \frac{1}{2 x}$ and q(x) = 12

For an equation in standard form, the integrating factor is $e^{\int p (x) d x}$

How do I use an integrating factor to solve a differential equation?

STEP 1: If necessary, rearrange the differential equation into standard form
STEP 2: Find the integrating factor

Note that you don’t need to include a constant of integration here when you integrate ∫p(x) dx

STEP 3: Multiply both sides of the differential equation by the integrating factor

This will turn the equation into an exact differential equation of the form $\frac{d}{d x} (y e^{\int p (x) d x}) = q (x) e^{\int p (x) d x}$

STEP 4: Integrate both sides of the equation with respect to x

The left side will automatically integrate to $y e^{\int p (x) d x}$
For the right side, integrate $\int q (x) e^{\int p (x) d x} d x$ using your usual techniques for integration
Don’t forget to include a constant of integration

Although there are two integrals, you only need to include one constant of integration

STEP 5: Rearrange your solution to get it in the form y = f(x)

What else should I know about using an integrating factor to solve differential equations?

After finding the general solution using the steps above you may be asked to do other things with the solution

For example you may be asked to find the solution corresponding to certain initial or boundary conditions

Worked Example

Consider the differential equation $\frac{d y}{d x} = 2 x y + 5 e^{x^{2}}$ where y = 7 when x = 0.

Use an integrating factor to find the solution to the differential equation with the given boundary condition.

5-10-2-ib-aa-hl-integrating-factor-we-solution

DP IB Maths: AA HL

Revision Notes

5.10.2 Analytical Solutions to Differential Equations

Separation of Variables

What is separation of variables?

How do I solve a differential equation using separation of variables?

Exam Tip

Worked Example

Homogeneous Differential Equations

What is a homogeneous first order differential equation?

How do I solve a homogeneous first order differential equation?

What else should I know about solving homogeneous first order differential equations?

Exam Tip

Worked Example

Integrating Factor

What is an integrating factor?

How do I use an integrating factor to solve a differential equation?

What else should I know about using an integrating factor to solve differential equations?

Worked Example

Author: Roger

Resources

Members

Company

Quick Links