l'Hôpital's Rule
What is l’Hôpital’s Rule?
- l’Hôpital’s rule is a method involving calculus that allows us to find the value of certain limits
- Specifically, it allows us to attempt to evaluate the limit of a quotient
for which our usual limit evaluation techniques would return one of the indeterminate forms
or
.
How do I evaluate a limit using l’Hôpital’s Rule?
- STEP 1: Check that the limit of the quotient results in one of the indeterminate forms given above
- I.e., check that
or
- STEP 2: Find the derivatives of the numerator and denominator of the quotient
- STEP 3: Check whether the limit
exists
- STEP 4: If that limit does exist, then
- STEP 5: If
or
then you may repeat the process by considering
(and possibly higher order derivatives after that)
- As long as the limits continue giving indeterminate forms you may continue applying l’Hôpital’s rule
- Each time this happens find the next set of derivatives and consider the limit again
Exam Tip
- Some limits of an indeterminate form can also be evaluated using the Maclaurin series for the numerator and denominator
- If an exam question does not specify a method to use, then you are free to use whichever method you prefer
Worked Example
Use l’Hôpital’s rule to evaluate each of the following limits:
a) .
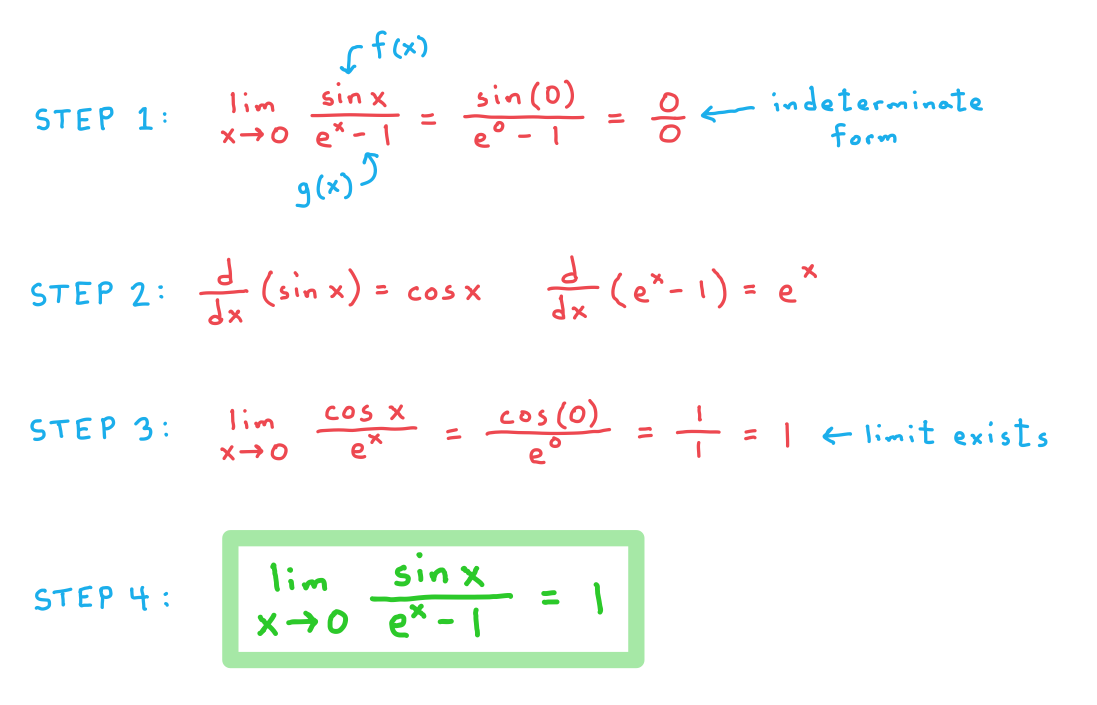
b) .

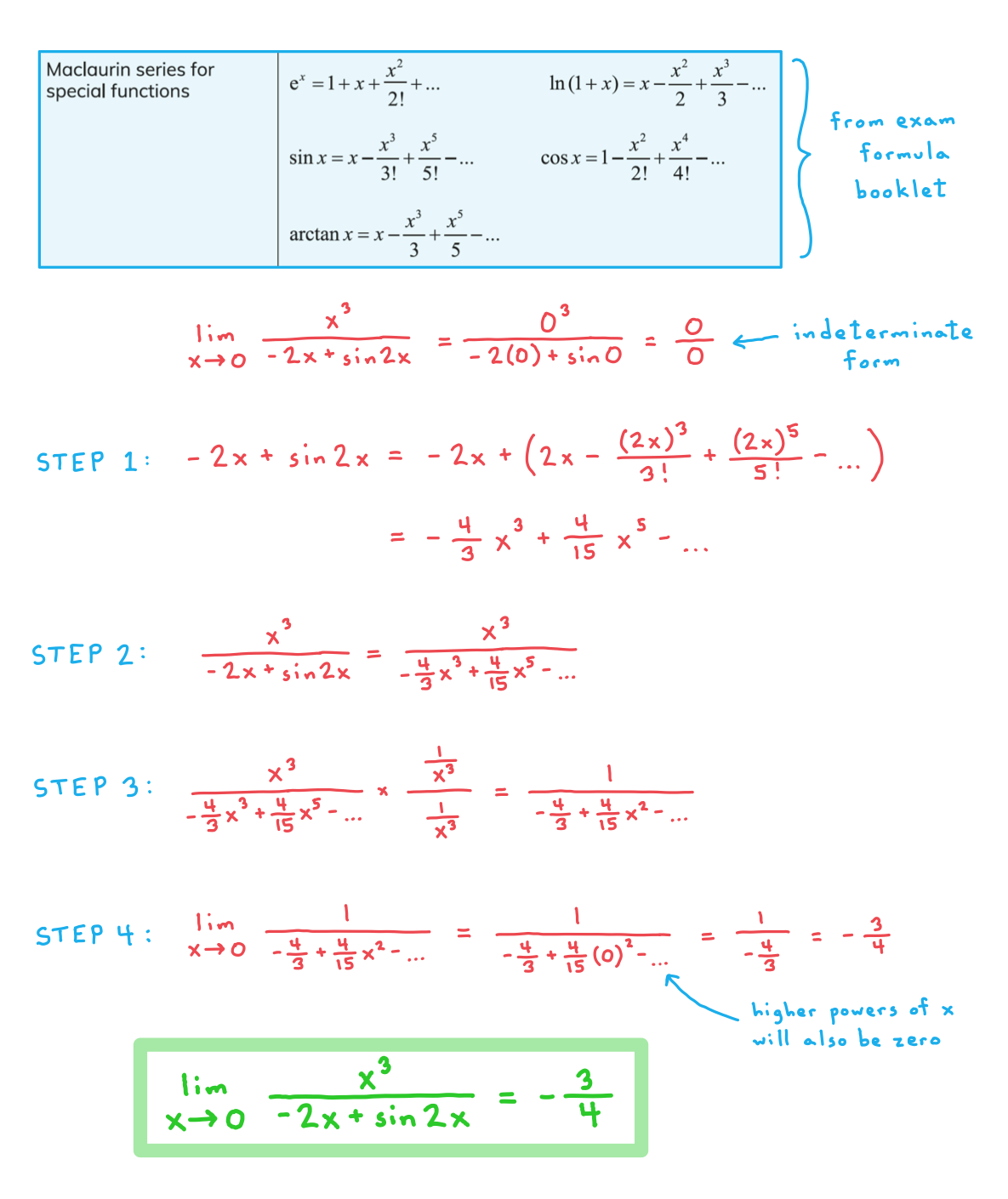
Limits Using a Maclaurin Series
How do I evaluate a limit using Maclaurin series?
- Limits of the form
or
may sometimes be evaluated by using Maclaurin series
- Usually this will be in a situation where attempting to evaluate the limit in the usual way returns an indeterminate form
or
.
- In such a case:
- STEP 1: Find the Maclaurin series for
and
- STEP 2: Rewrite
using the Maclaurin series in the numerator and denominator
- STEP 3: Use algebra to simplify your new expression for
as far as possible
- STEP 4: Evaluate the limit using your simplified form of the expression
Exam Tip
- Some limits of an indeterminate form can also be evaluated using l’Hôpital’s Rule
- If an exam question does not specify a method to use, then you are free to use whichever method you prefer
Worked Example
Use Maclaurin series to evaluate the limit