Reciprocal Trig Functions
What are the reciprocal trig functions?
- There are three reciprocal trig functions that each correspond to either sin, cos or tan
- Secant (sec x)
-
- Cosecant (cosec x)
- Cotangent (cot x)
- The identities above for sec x and cosec x are given in the formula booklet
- The identity for cot x is not given, you will need to remember it
- A good way to remember which function is which is to look at the third letter in each of the reciprocal trig functions
- cot x is 1 over tan x etc
- Secant (sec x)
- Each of the reciprocal trig functions are undefined for certain values of x
- sec x is undefined for values of x for which cos x = 0
- cosec x is undefined for values of x for which sin x = 0
- cot x is undefined for values of x for which tan x = 0
- When tan x is undefined, cot x = 0
- Rearranging the identity
gives
- This is not in the formula booklet but is easily derived
- Be careful not to confuse the reciprocal trig functions with the inverse trig functions
What do the graphs of the reciprocal trig functions look like?
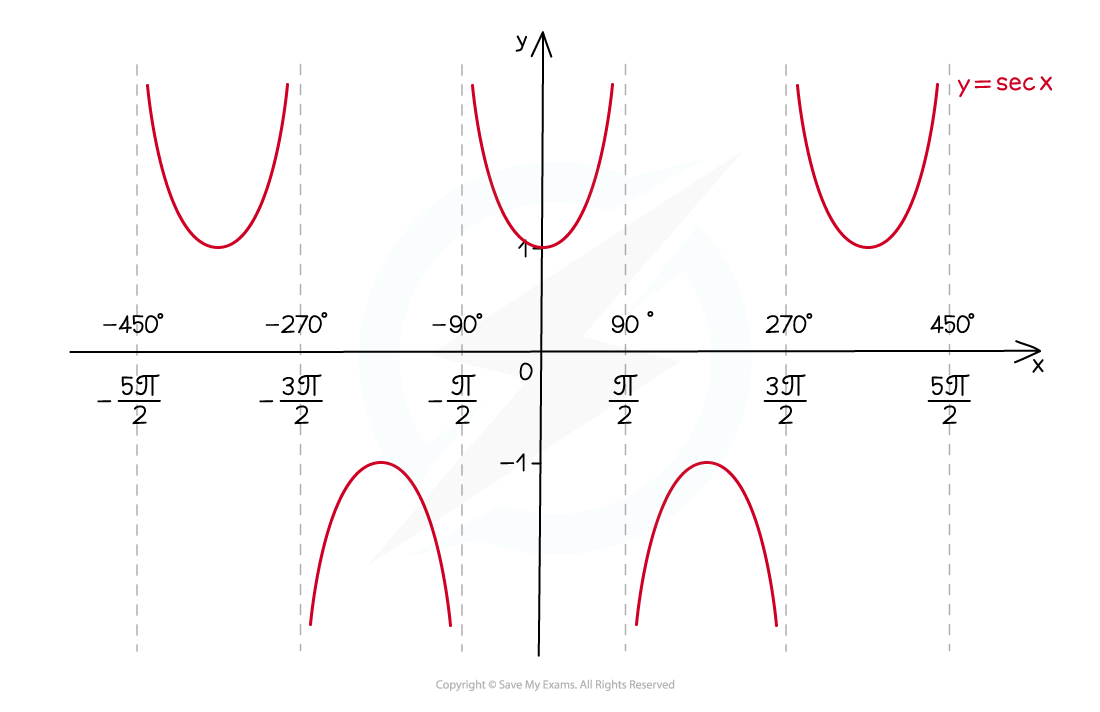
- The graph of y = secx has the following properties:
- The y-axis is a line of symmetry
- It has a period of 360° (2π radians)
- There are vertical asymptotes wherever cos x = 0
- If drawing the graph without the help of a GDC it is a good idea to sketch cos x first and draw these in
- The domain is all x except odd multiples of 90° (90°, -90°, 270°, -270°, etc.)
- in radians this is all x except odd multiples of π/2 (π/2, - π/2, 3π/2, -3π/2, etc.)
- The range is y ≤ -1 or y ≥ 1
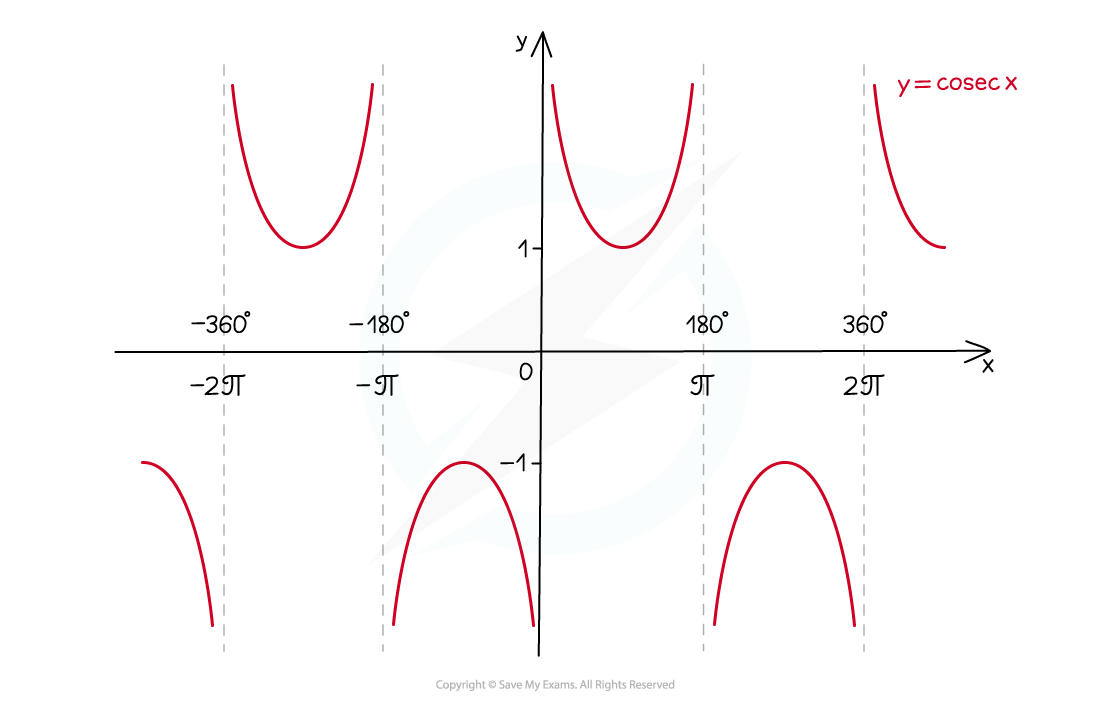
- The graph of y = cosec x has the following properties:
- It has a period of 360° (2π radians)
- There are vertical asymptotes wherever sin x = 0
- If drawing the graph it is a good idea to sketch sin x first and draw these in
- The domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)
- in radians this is all x except multiples of π (0, π, - π, 2π, -2π, etc.)
- The range is y ≤ -1 or y ≥ 1
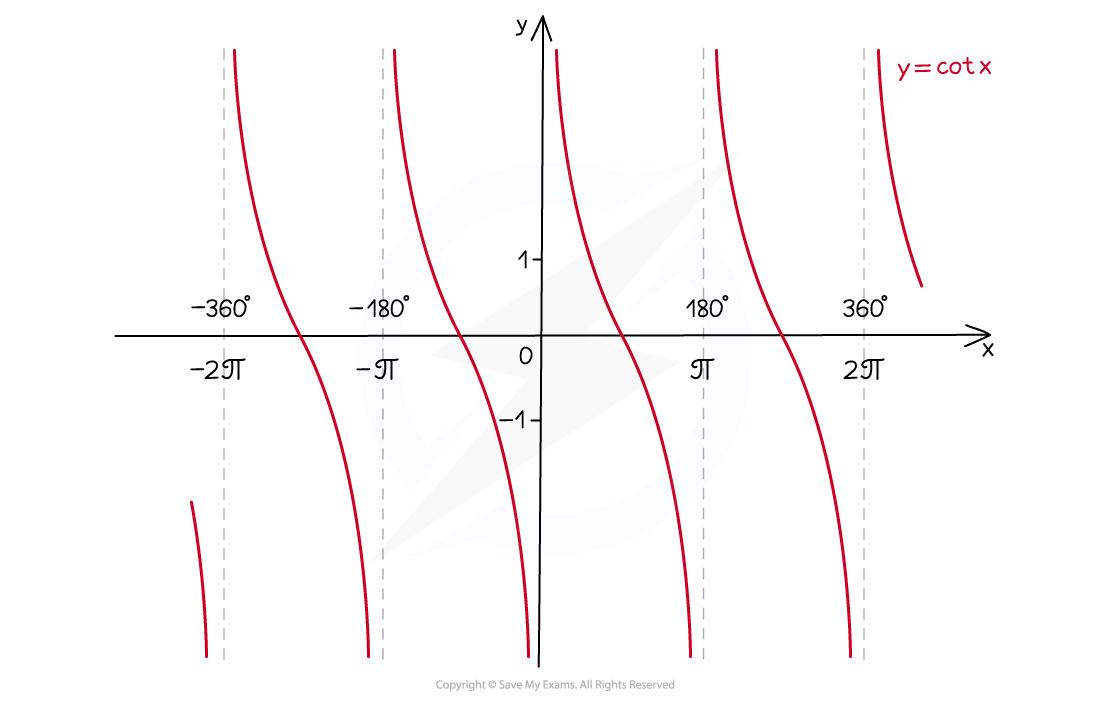
- The graph of y = cot x has the following properties
- It has a period of 180° or π radians
- There are vertical asymptotes wherever tan x = 0
- The domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)
- In radians this is all x except multiples of π (0, π, - π, 2π, -2π, etc.)
- The range is y ∈ ℝ (i.e. cot can take any real number value)
Exam Tip
- To solve equations with the reciprocal trig functions, convert them into the regular trig functions and solve in the usual way
- Don't forget that both tan and cot can be written in terms of sin and cos
- You will sometimes see csc instead of cosec for cosecant
Worked Example
Without the use of a calculator, find the values of
a)
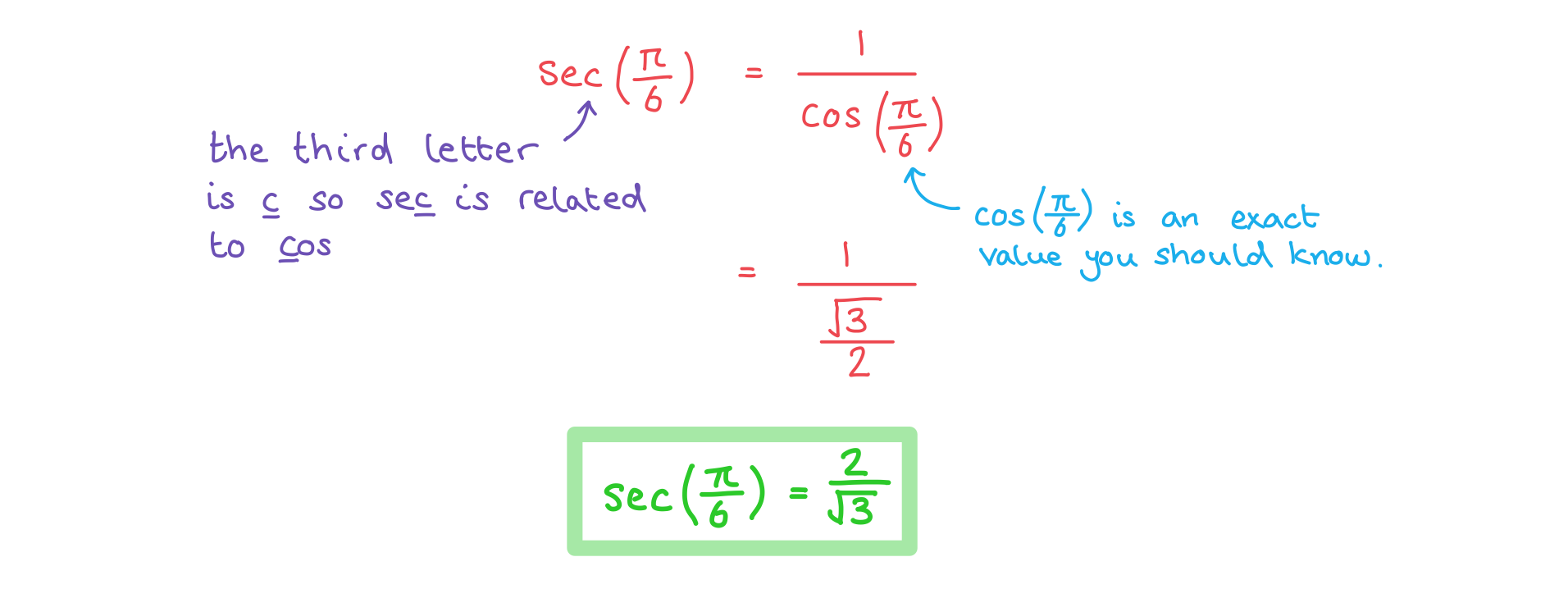
b)

Pythagorean Identities
What are the Pythagorean Identities?
- Aside from the Pythagorean identity sin2x + cos2x = 1 there are two further Pythagorean identities you will need to learn
-
-
- Both can be found in the formula booklet
- Both of these identities can be derived from sin2x + cos2x = 1
- To derive the identity for sec2x divide sin2x + cos2x = 1 by cos2x
- To derive the identity for cosec2x divide sin2x + cos2x = 1 by sin2x
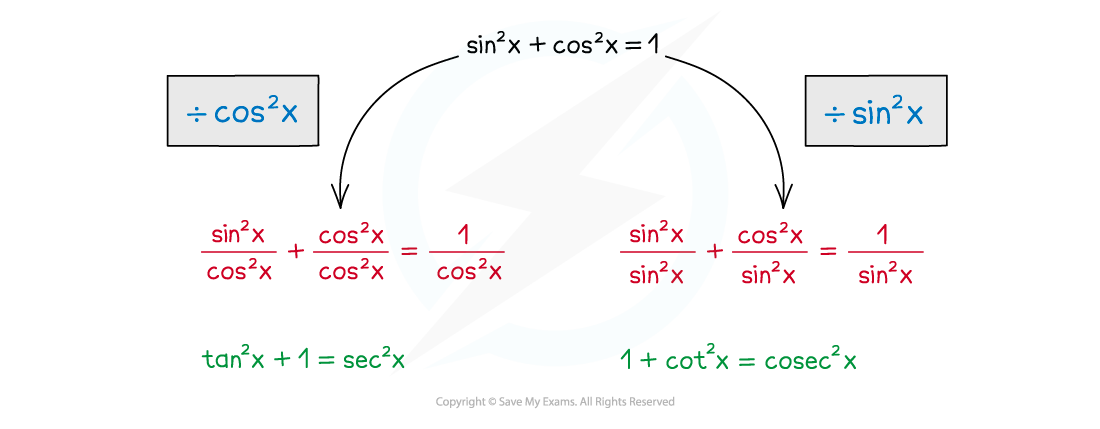
Exam Tip
All the Pythagorean identities can be found in the Topic 3: Geometry and Trigonometry section of the formula booklet
Worked Example
Solve the equation 9 sec2 θ – 11 = 3 tan θ in the interval 0 ≤ θ ≤ 2π.

