Modulus Transformations
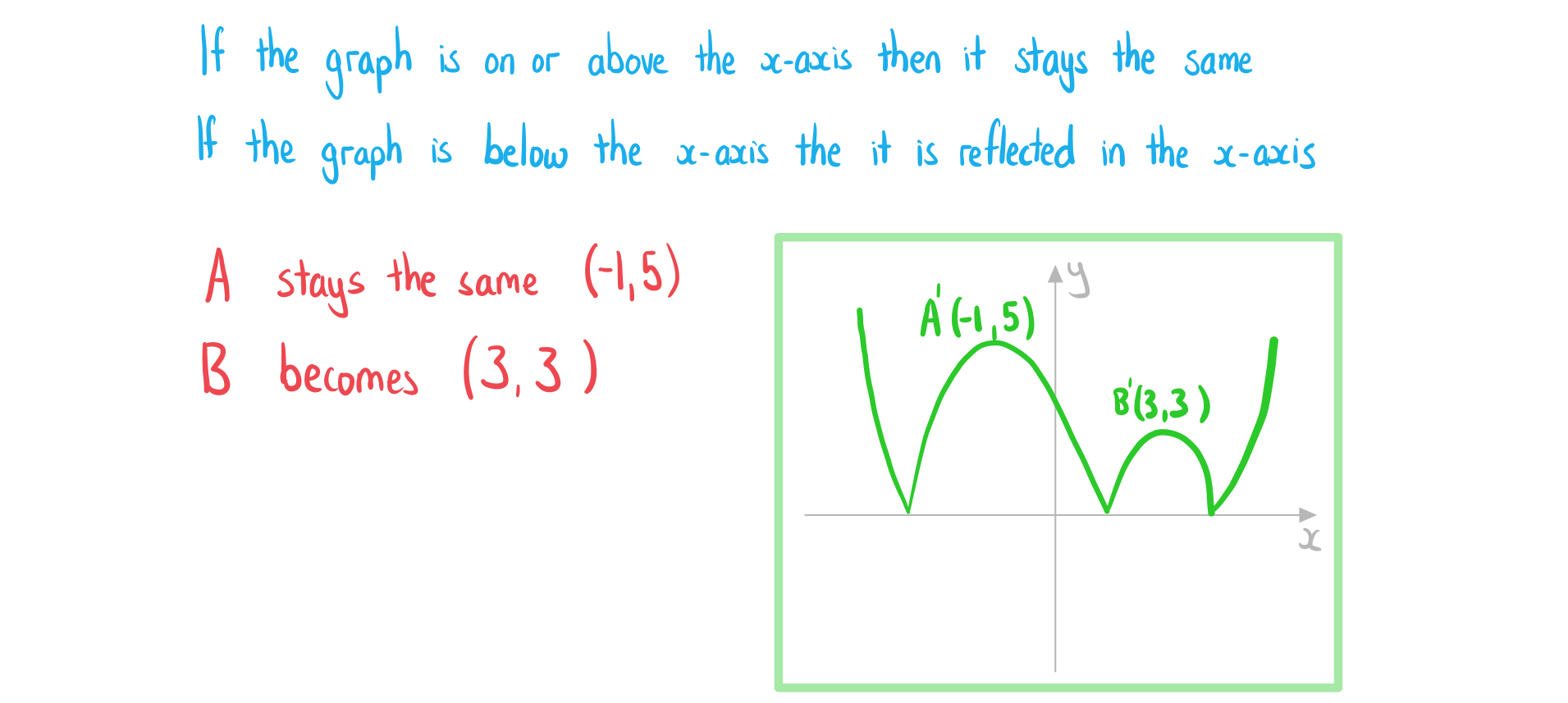
How do I sketch the graph of the modulus of a function: y = |f(x)|?
- STEP 1: Keep the parts of the graph of y = f(x) that are on or above the x-axis
- STEP 2: Any parts of the graph below the x-axis get reflected in the x-axis anything
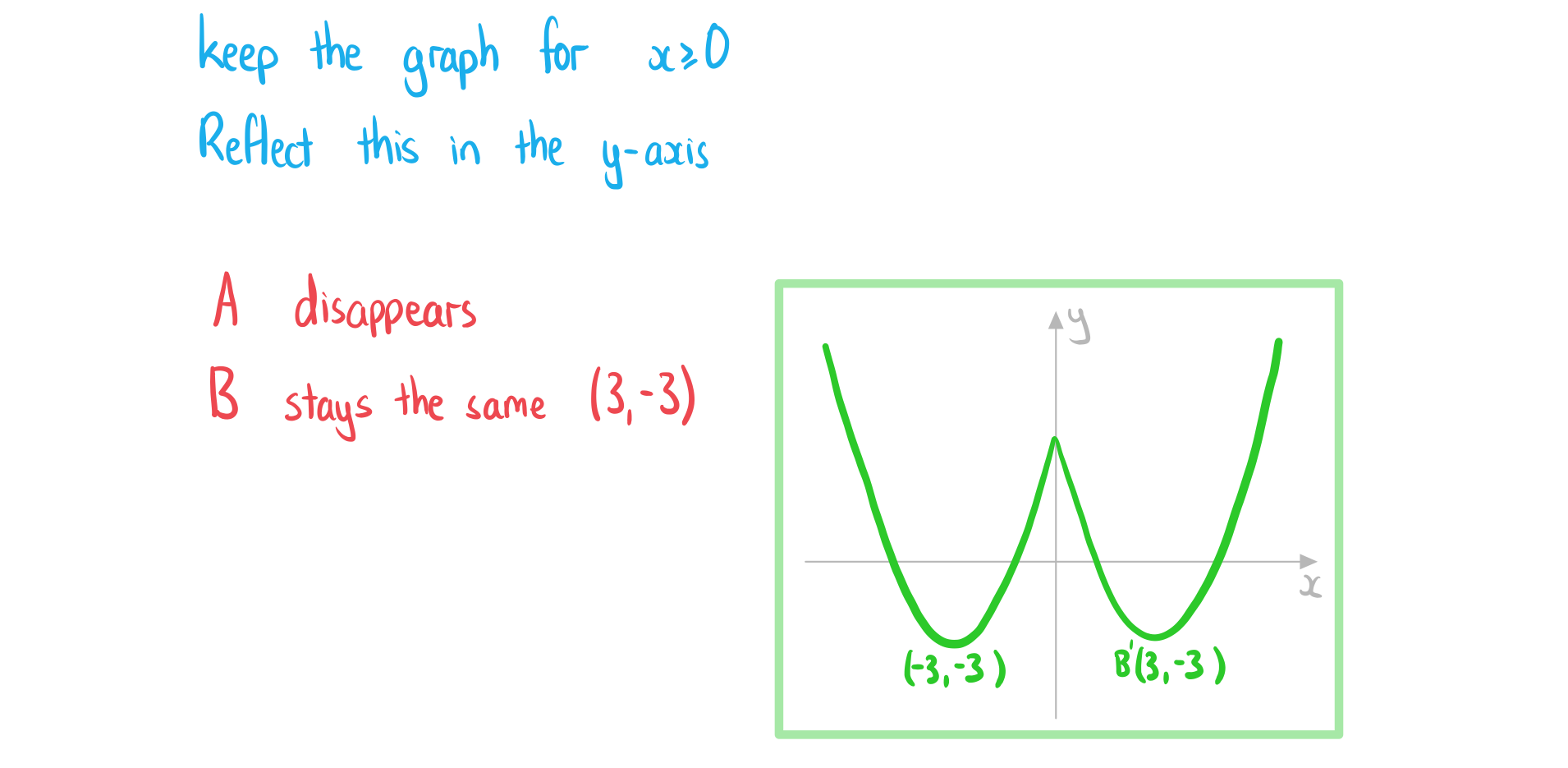
How do I sketch the graph of a function of a modulus: y = f(|x|)?
- STEP 1: Keep the graph of y = f(x) only for x ≥ 0
- STEP 2: Reflect this in the y-axis
What is the difference between y = |f(x)| and y = f(|x|)?
- The graph of y = |f(x)| never goes below the x-axis
- It does not have to have any lines of symmetry
- The graph of y = f(|x|) is always symmetrical about the y-axis
- It can go below the y-axis
When multiple transformations are involved how do I determine the order?
- The transformations outside the function follow the same order as the order of operations
- Deal with the a then the b then the modulus
- Deal with the modulus then the a then the b
- The transformations inside the function are in the reverse order to the order of operations
- Deal with the modulus then the b then the a
- Deal with the b then the a then the modulus
Exam Tip
- When sketching one of these transformations in an exam question make sure that the graphs do not look smooth at the points where the original graph have been reflected
- For
the graph should look "sharp" at the points where it has been reflected on the x-axis
- For
the graph should look "sharp" at the point where it has been reflected on the y-axis
- For
Worked Example
The diagram below shows the graph of .
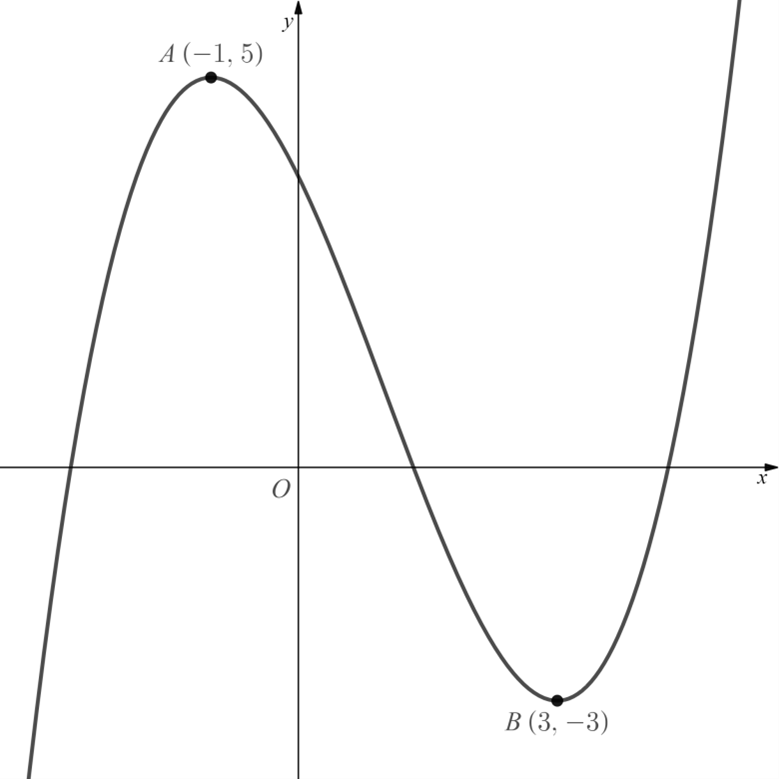
(a) Sketch the graph of .
(b) Sketch the graph of .