Derivatives & Graphs
How are derivatives and graphs connected?
- If the graph of a function
is known, or can be sketched, then it is also possible to sketch the graphs of the derivatives
and
- The key properties of a graph include
- the
-axis intercept
- the
-axis intercepts – the roots of the function; where
- stationary points; where
- turning points – (local) minimum and maximum points
- (horizontal) points of inflection
- (non-stationary,
) points of inflection
- asymptotes – vertical and horizontal
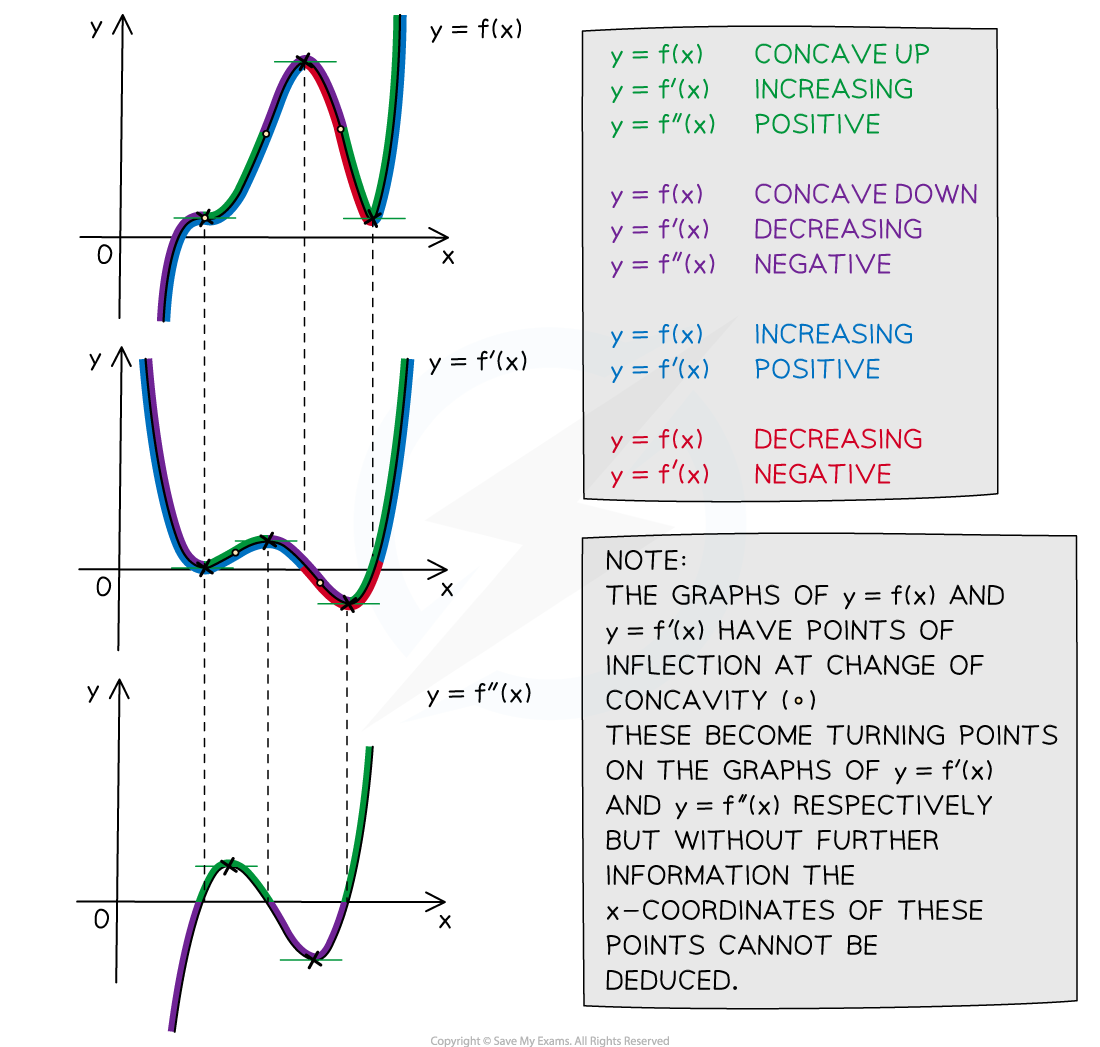
- intervals where the graph is increasing and decreasing
- intervals where the graph is concave down and concave up
- the
- Not all graphs have all of these properties and not all can be determined without knowing the expression of the function
- However questions will provide enough information to sketch
- the shape of the graph
- some of the key properties such as roots or turning points
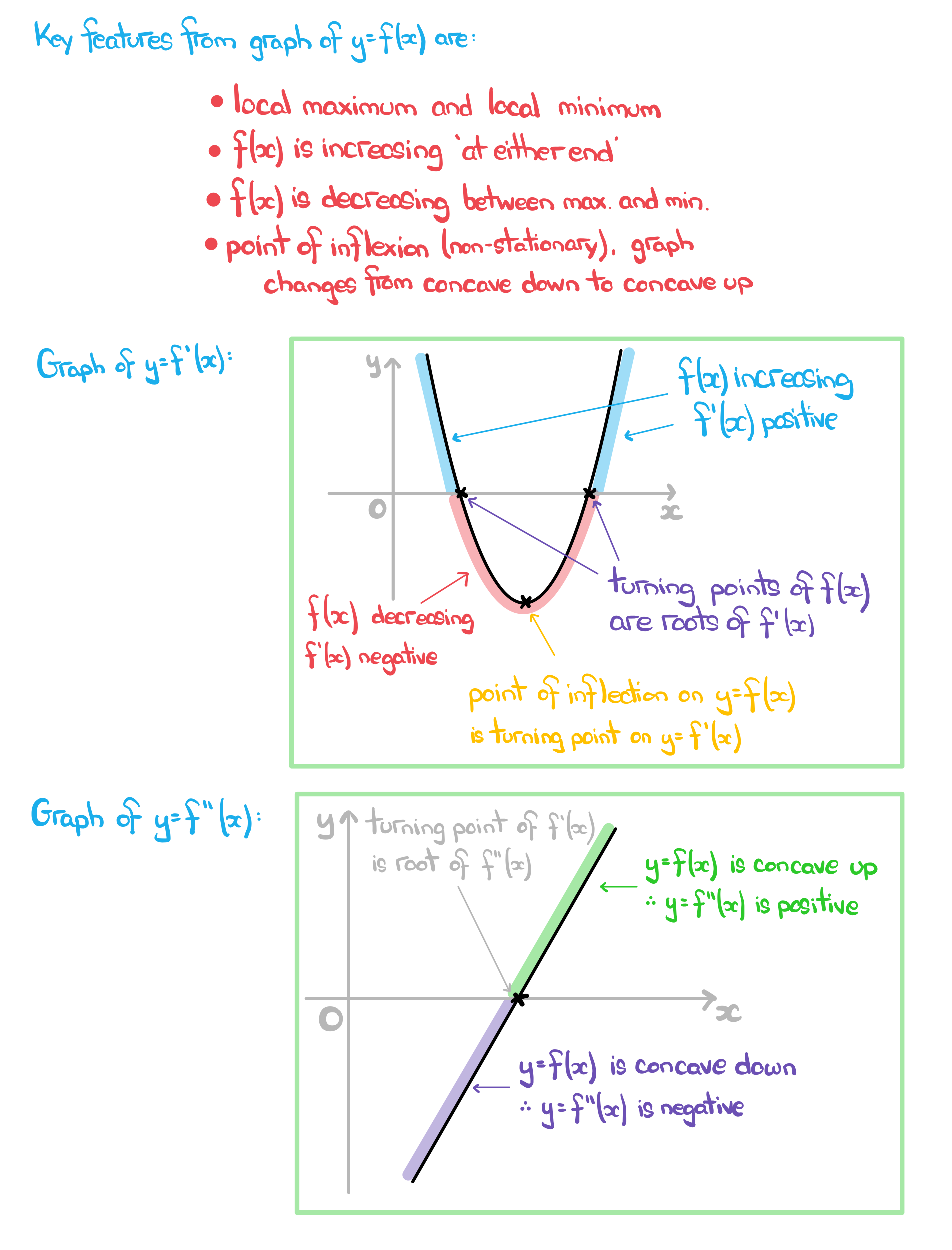
How do I sketch the graph of y = f'(x) from the graph of y = f(x)?
- The graph of
will have its
-axis intercepts at the
-coordinates of the stationary points of
- turning points at the
-coordinates of the points of inflection of
- For intervals where
is concave up,
will be increasing
- For intervals where
is concave down ,
will be decreasing
- For intervals where
is increasing,
will be positive
- For intervals where
is decreasing,
will be negative
How do I sketch the graph of y = f''(x) from the graph of y = f(x)?
- First sketch the graph of
from
, as per the above process
- Then, using the same process, sketch the graph of
from the graph of
- There are a couple of things you can deduce about the graph of
directly from the graph of
- The graph of
will have its
-axis intercepts at the
-coordinates of the points of inflection of
- For intervals where
is concave up,
will be positive
- For intervals where
is concave down,
will be negative
- The graph of
Is it possible to sketch the graph of y = f(x) from the graph of a derivative?
- It is possible to sketch a graph of
by considering the reverse of the above
- For intervals where
is positive,
will be increasing but is not necessarily positive
- For intervals where
is negative,
will be decreasing but is not necessarily negative
- Roots of
give the
-coordinates of the stationary points of
- For intervals where
- There are some properties of the graph of
that cannot be determined from the graph of
- the
-axis intercept
- the intervals for which
is positive and negative
- the roots of
- the
- Unless a specific point the curve passes through is known, the constant of integration cannot be determined
- the exact location of the curve will remain unknown
- but it will still be possible to sketch its shape
- If starting from the graph of the second derivative,
, it is easier to sketch the graph of
first, then sketch
Worked Example
The graph of is shown in the diagram below.

On separate diagrams sketch the graphs of and
, labelling any roots and turning points.