Name: Strategy for Trigonometric Equations (3.8.2) | DP IB Maths: AA HL Revision Notes 2021 Membership
Brand: Save My Exams
Price: 60 GBP
Availability: OnlineOnly
Rating: 4.7 (1021 reviews)

3.8.2 Strategy for Trigonometric Equations

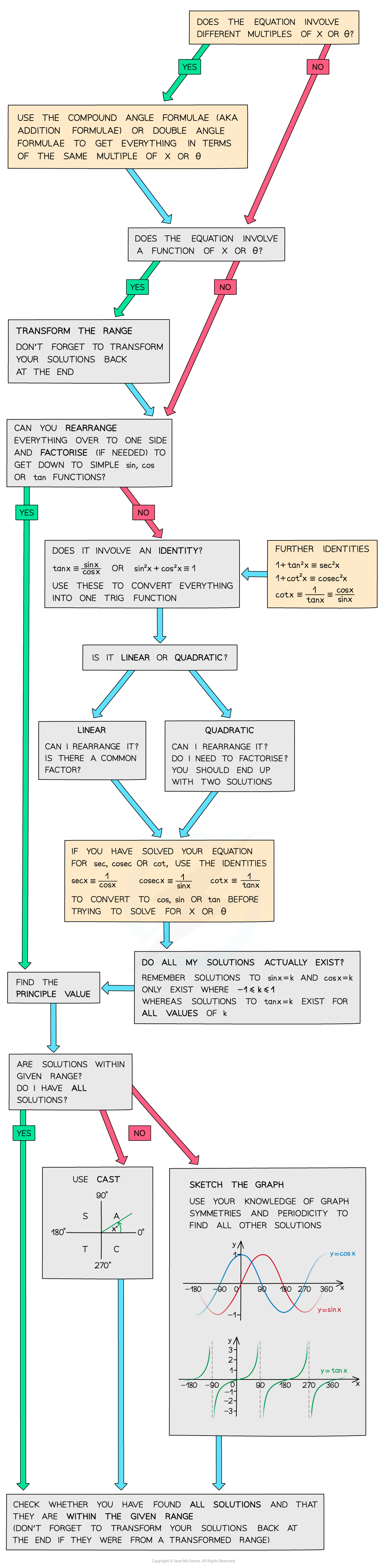
Strategy for Trigonometric Equations

How do I approach solving trig equations?

You can solve trig equations in a variety of different ways

Sketching a graph

If you have your GDC it is always worth sketching the graph and using this to analyse its features

Using trigonometric identities, Pythagorean identities, the compound or double angle identities

Almost all of these are in the formula booklet, make sure you have it open at the right page

Using the unit circle
Factorising quadratic trig equations

Look out for quadratics such as 5tan²x – 3tan x – 4 = 0

The final rearranged equation you solve will involve sin, cos or tan

Don’t try to solve an equation with cosec, sec, or cot directly

What should I look for when solving trig equations?

Check the value of x or θ

If it is just x or θ you can begin solving
If there are different multiples of x or θ you will need to use the double angle formulae to get everything in terms of the same multiple of x or θ
If it is a function of x or θ, e.g. 2x – 15, you will need to transform the range first

You must remember to transform your solutions back again at the end

Does it involve more than one trigonometric function?

If it does, try to rearrange everything to bring it to one side, you may need to factorise
If not, can you use an identity to reduce the number of different trigonometric functions?

You should be able to use identities to reduce everything to just one simple trig function (either sin, cos or tan)

Is it linear or quadratic?

If it is linear you should be able to rearrange and solve it
If it is quadratic you may need to factorise first

You will most likely get two solutions, consider whether they both exist
Remember solutions to sin x = k and cos x = k only exist for -1 ≤ k ≤ 1 whereas solutions to tan x = k exist for all values of k

Are my solutions within the given range and do I need to find more solutions?

Be extra careful if your solutions are negative but the given range is positive only
Use a sketch of the graph or the unit circle to find the other solutions within the range
If you have a function of x or θ make sure you are finding the solutions within the transformed range

Don’t forget to transform the solutions back so that they are in the required range at the end

Strategy for Further Trigonometric Equations Diagram 1

Exam Tip

Try to use identities and formulas to reduce the equation into its simplest terms.
Don’t forget to check the function range and ensure you have included all possible solutions.
If the question involves a function of x or θ ensure you transform the range first (and ensure you transform your solutions back again at the end!).

Worked Example

Find the solutions of the equation $(1 + \cot^{2} 2 θ) (5 \cos^{2} θ - 1) = \cot^{2} 2 θ$ in the interval $0 \leq θ \leq 2 π$ .

3-8-2-ib-aa-hl-equation-strategy-we-solution

DP IB Maths: AA HL

Revision Notes

3.8.2 Strategy for Trigonometric Equations

Strategy for Trigonometric Equations

How do I approach solving trig equations?

What should I look for when solving trig equations?

Exam Tip

Worked Example

Author: Amber

Resources

Members

Company

Quick Links