Name: Polynomial Division (2.7.2) | DP IB Maths: AA HL Revision Notes 2021 Membership
Brand: Save My Exams
Price: 60 GBP
Availability: OnlineOnly
Rating: 4.7 (1021 reviews)

2.7.2 Polynomial Division

Polynomial Division

What is polynomial division?

Polynomial division is the process of dividing two polynomials
- This is usually only useful when the degree of the denominator is less than or equal to the degree of the numerator
To do this we use an algorithm similar to that used for division of integers
To divide the polynomial $P (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{1} x + a_{0}$ by the polynomial $D (x) = b_{k} x^{k} + b_{k - 1} x^{k - 1} + . . . + b_{1} x + b_{0}$ where k ≤ n
- STEP 1
  Divide the leading term of the polynomial P(x) by the leading term of the divisor D(x) : $\frac{a_{n} x^{n}}{b_{b} x^{k}} = q_{m} x^{m}$
- STEP 2
  Multiply the divisor by this term: $D (x) \times q_{m} x^{m}$
- STEP 3
  Subtract this from the original polynomial P(x) to cancel out the leading term: $R (x) = P (x) - D (x) \times q_{m} x^{m}$
- Repeat steps 1 – 3 using the new polynomial R(x) in place of P(x) until the subtraction results in an expression for R(x) with degree less than the divisor
  - The quotient Q(x) is the sum of the terms you multiplied the divisor by: $Q (x) = q_{m} x^{m} + q_{m - 1} x^{m - 1} + . . . + q_{1} x + q_{0}$
  - The remainder R(x) is the polynomial after the final subtraction

Division by linear functions

If P(x) has degree n and is divided by a linear function (ax + b) then

$\frac{P (x)}{a x + b} = Q (x) + \frac{R}{a x + b}$ where

ax + b is the divisor (degree 1)
Q(x) is the quotient (degree n – 1)
R is the remainder (degree 0)

Note that $P (x) = Q (x) \times (a x + b) + R$

Division by quadratic functions

If P(x) has degree n and is divided by a quadratic function (ax² + bx + c) then

$\frac{P (x)}{a x^{2} + b x + c} = Q (x) + \frac{e x + f}{a x^{2} + b x + c}$ where

ax² + bx + c is the divisor (degree 2)
Q(x) is the quotient (degree n – 2)
ex + f is the remainder (degree less than 2)

The remainder will be linear (degree 1) if e ≠ 0, and constant (degree 0) if e = 0
Note that $P (x) = Q (x) \times (a x^{2} + b x + c) + e x + f$

Division by polynomials of degree k ≤ n

If P(x) has degree n and is divided by a polynomial D(x) with degree k ≤ n
- $\frac{P (x)}{D (x)} = Q (x) + \frac{R (x)}{D (x)}$ where
  - D(x) is the divisor (degree k)
  - Q(x) is the quotient (degree n – k)
  - R(x) is the remainder (degree less than k)
- Note that $P (x) = Q (x) \times D (x) + R (x)$

Are there other methods for dividing polynomials?

Synthetic division is a faster and shorter way of setting out a division when dividing by a linear term of the form

To divide $P (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{1} x + a_{0}$ by $(x - c)$ :

Set $b_{n} = a_{n}$
Calculate $b_{n - 1} = a_{n - 1} + c \times b_{n}$
Continue this iterative process $b_{i - 1} = a_{i - 1} + c \times a_{i}$
The quotient is $Q (x) = b_{n} x^{n - 1} + b_{n - 1} x^{n - 2} + . . . + b_{2} x + b_{1}$ and the remainder is $r = b_{0}$

You can also find quotients and remainders by comparing coefficients

Given a polynomial $P (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{1} x + a_{0}$
And a divisor $D (x) = d_{k} x^{k} + d_{k - 1} x^{k - 1} + . . . + d_{1} x + d_{0}$
Write $Q (x) = q_{n - k} x^{n - k} + . . . + q_{1} x + q_{0}$ and $R (x) = r_{k - 1} x^{k - 1} + . . . + r_{1} x + r_{0}$
Write $P (x) = Q (x) D (x) + R (x)$

Expand the right-hand side
Equate the coefficients
Solve to find the unknowns q’s & r’s

Exam Tip

In an exam you can use whichever method to divide polynomials - just make sure your method is written clearly so that if you make a mistake you can still get a mark for your method!

Worked Example

Perform the division

\frac{x^{4} + 11 x^{2} - 1}{x + 3}

. Hence write

x^{4} + 11 x^{2} - 1

in the form

Q (x) \times (x + 3) + R

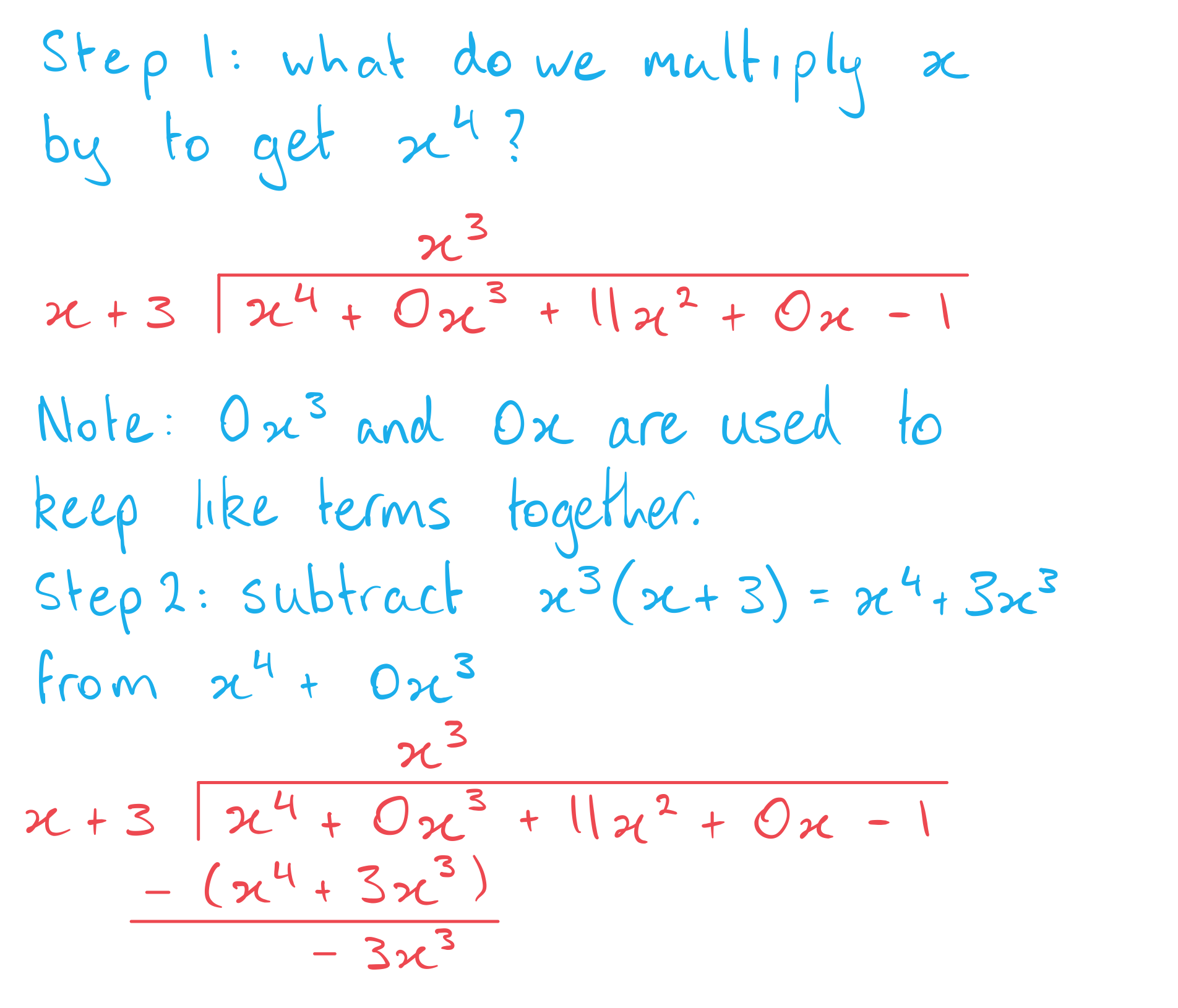
2-7-2-ib-aa-hl-polynomial-division-a-we-solution-1-2

Find the quotient and remainder for

\frac{x^{4} + 4 x^{3} - x + 1}{x^{2} - 2 x}

. Hence write

x^{4} + 4 x^{3} - x + 1

in the form

Q (x) \times (x^{2} - 2 x) + R (x)

2-7-2-ib-aa-hl-polynomial-division-b-we-solution-

DP IB Maths: AA HL

Revision Notes

2.7.2 Polynomial Division

Polynomial Division

What is polynomial division?

Division by linear functions

Division by quadratic functions

Division by polynomials of degree k ≤ n

Are there other methods for dividing polynomials?

Exam Tip

Worked Example

Author: Lucy

Resources

Members

Company

Quick Links